5G-s-P1 5G-Newton Lines Crosspoint
Given a pentagon P1P2P3P4P5.
We denote the intersection of P1P3 and P2P5 by P12.
Similarly P23, P34, P45 and P51 are defined.
The 5 Newton lines of P1P12P2P4, P2P23P3P5, P3P34P4P1, P4P45P5P2 and P5P51P1P3 have a common point 5G-s-P1.
See [34], Seiichi Kirikami, QFG#760.
There is another way to construct this point:
Given a pentagon P1P2P3P4P5.
We denote the intersection of P1P3 and P2P5 by P12.
Similarly P23, P34, P45 and P51 are defined.
We denote the midpoints of PiPi+1 by Mi+3
We denote the midpoints of PiPi+2 by mi. The lines Mimi concur in 5G-s-P1.
See [34], Seiichi Kirikami, QFG#726.
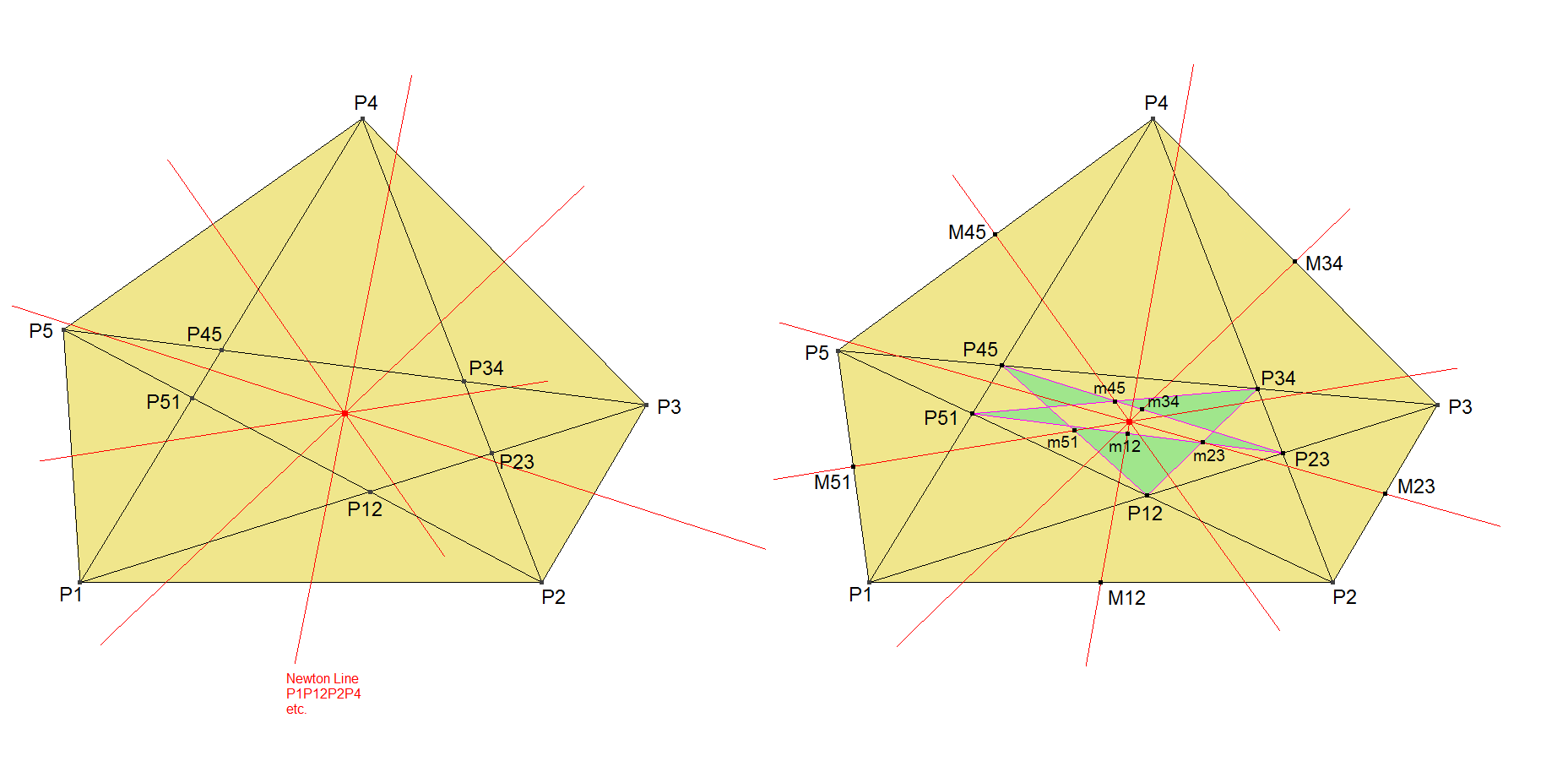
Note that the Newton Line in the left figure coincides with the lines Mimi in the right figure.
Coordinates:
Let P1,P2,P3,P4,P5 have these barycentric coordinates:
P1=(0:1:0), P2=(0:0:1), P3=(1:0:0), P4=(p:q:r) and P5=(P:Q:R).
Then 5G-s-P1 has coordinates: (p (2 P + Q) + P (q + r) : P q + p Q + q (2 Q + R) : P r + q R)
Calculation Seiichi Kirikami. See [34], QFG#750.
Properties
- 5G-s-P1, 5G-s-P2, 5G-s-P5 and 5L-s-P1 are collinear.
- 5G-s-P1 is the 4th harmonic point of 5L-s-P1 wrt 5G-s-P2 and 5G-s-P5 for every 5G-version of a 5-Line. See [66], QPG-message #1152.
Estimated human page views: 354
