5G-s-P4 5G-Miquel-Catalan Point
From [2d], page 4 comes this phrase (in the French language):
“En 1838, Auguste Miquel découvre à partir d’une idée d’Eugène Catalan, ”Le pentagramme” formé par cinq droites en position générale.“
The message is that Auguste Miquel discovered a special point originating from an idea of Eugène Catalan.
Construction
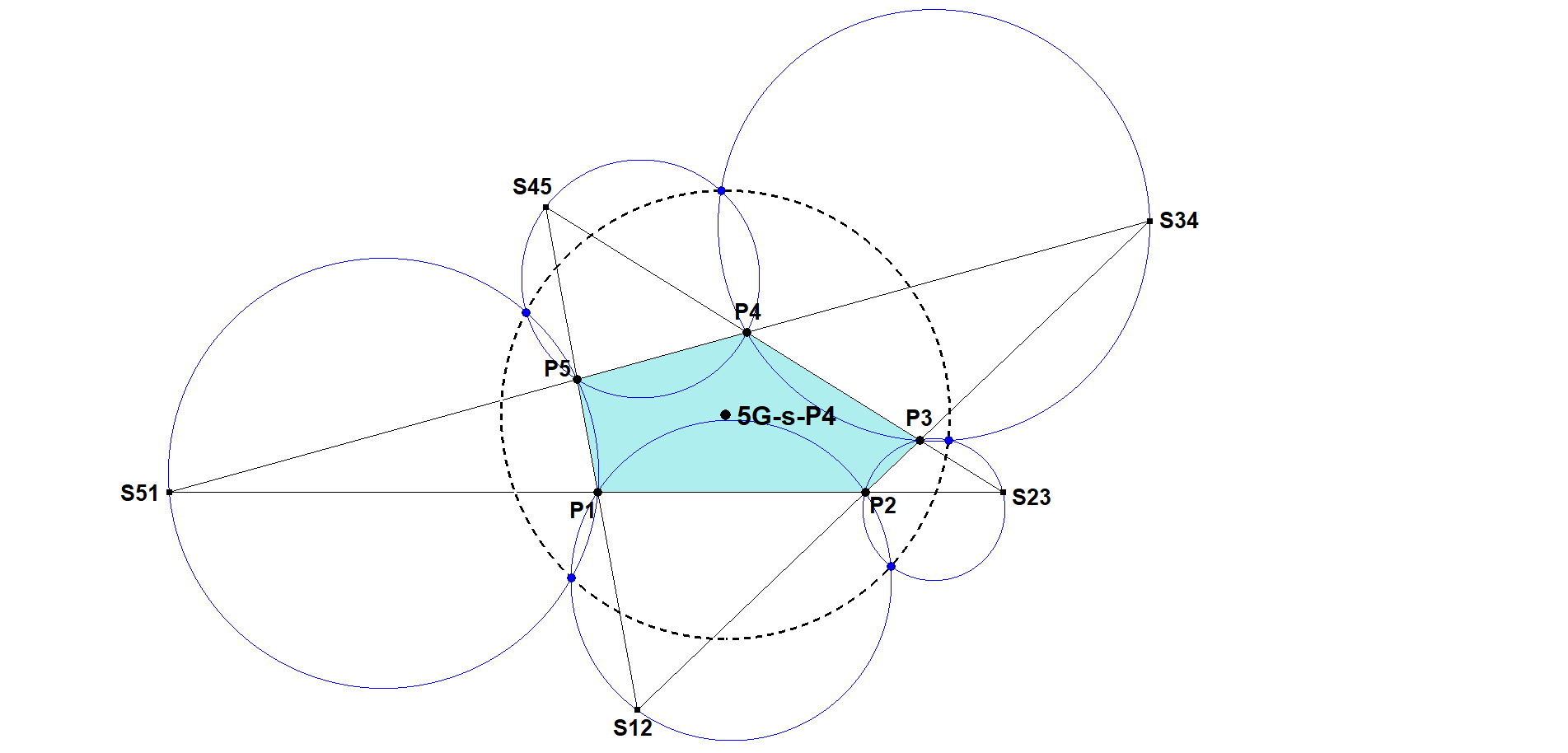
Let P1.P2.P3.P4.P5 be a pentagon and in combination with S12.S23.S34.S45.S51 form a Pentagram.
Consider the 5 circles: (S12,P3,P5), (S23,P4,P1), (S34,P5,P2), (S45,P1,P3), (S51,P2,P4).
The 2nd intersection points of each pair of these circles lie on a circle with center 5G-s-P4.
See also [70], page 1 and [13], keyword “Miquel’s Pentagram Theorem”.
Properties
- 5G-s-P4 is a special case of Clifford’s Circle Center 5L-o-P2, which is the 5L-version of nL-o-P2. Moreover the circle through the 2nd-intersection points is 5L-o-Ci1, which is the 5L-version of nL-o-Ci1: nL-Clifford’s Circle. See also Jean-Louis Ayme’s document.
- When the 5-Gon is considered a 5-Line (L1.L2.L3.L4.L5), then it will appear that the Miquel Point QL-P1 of each Component 4-Line (L1.L2.L3.L4, etc.) will coincide with a corresponding 2nd intersection point of a pair of the construction circles. Accidentally it is the circle through these 2nd intersection points the circle that defines 5G-s-P4, which explains why 5G-s-P4 = 5L-o-P2.
- When the 5-Gon is considered a 5-Point P1.P2.P3.P4.P5, then it will appear that the Miquel Point QL-P1 of each component 4-Point (P1.P2.P3.P4, etc.) will lie on a corresponding Pentagram circle.
- 5G-s-P4(P1.P3.P5.P2.P4) = 5G-s-P3(P1.P2.P3.P4.P5). See [66], QPG-message #1398.
- 5G-s-P4(P1.P2.P3.P4.P5) = 5G-s-P3(P1.P3.P5.P2.P4).
Estimated human page views: 231
