5G-s-P5 1st 5G-Hung’s Point
Let P1.P2.P3.P4.P5 be a pentagon and in combination with S12.S23.S34.S45.S51 form a Pentagram.
Consider the 5 circles: (S12,P3,P5), (S23,P4,P1), (S34,P5,P2), (S45,P1,P3), (S51,P2,P4).
The radical axes of each pair of these circles concur in one punt. This point is called 5G-s-P5 and was found by Tran Quang Hung. See [34], QFG#3654.
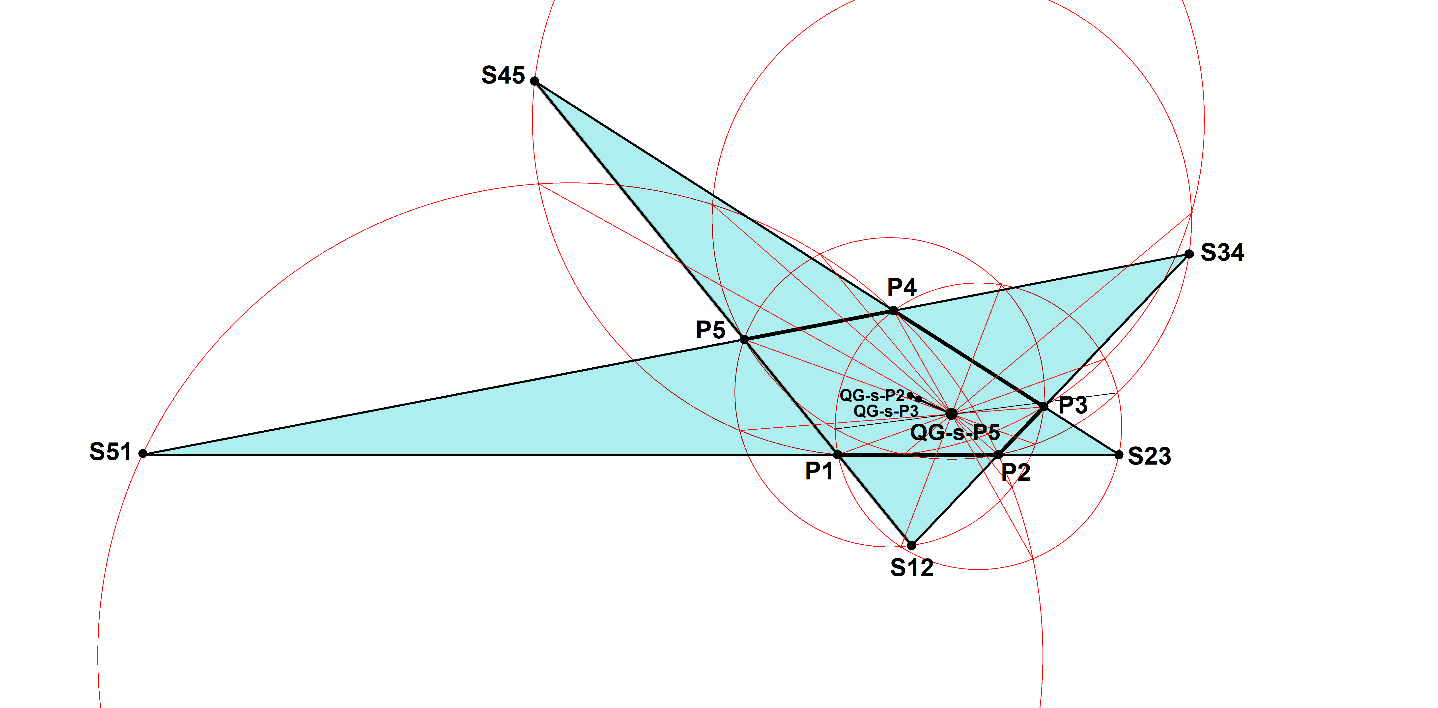
Properties
- 5G-s-P1, 5G-s-P2, 5G-s-P5 and 5L-s-P1 are collinear.
- 5G-s-P5 is the 4th harmonic point of 5G-s-P2 wrt 5G-s-P1 and 5L-s-P1 for every 5G-version of the 5L. See [66], QPG-message #1152.
- 5G-s-P5 lies on the orthogonal hyperbola 5G-s-Co1.
- 5G-s-P5(P1.P3.P5.P2.P4) = 5G-s-P2(P1.P2.P3.P4.P5). See [66], QPG-message #1398.
- 5G-s-P5(P1.P2.P3.P4.P5) = 5G-s-P2(P1.P3.P5.P2.P4).
Estimated human page views: 251
