5L-s-L2: 5L-Isoconjugate Line
5L-s-L2 is created by using the Quadrilateral transformation QL-Tf2 (Isoconjugation for Lines).
For an explanation of the notion of Isoconjugation see Ref-13.
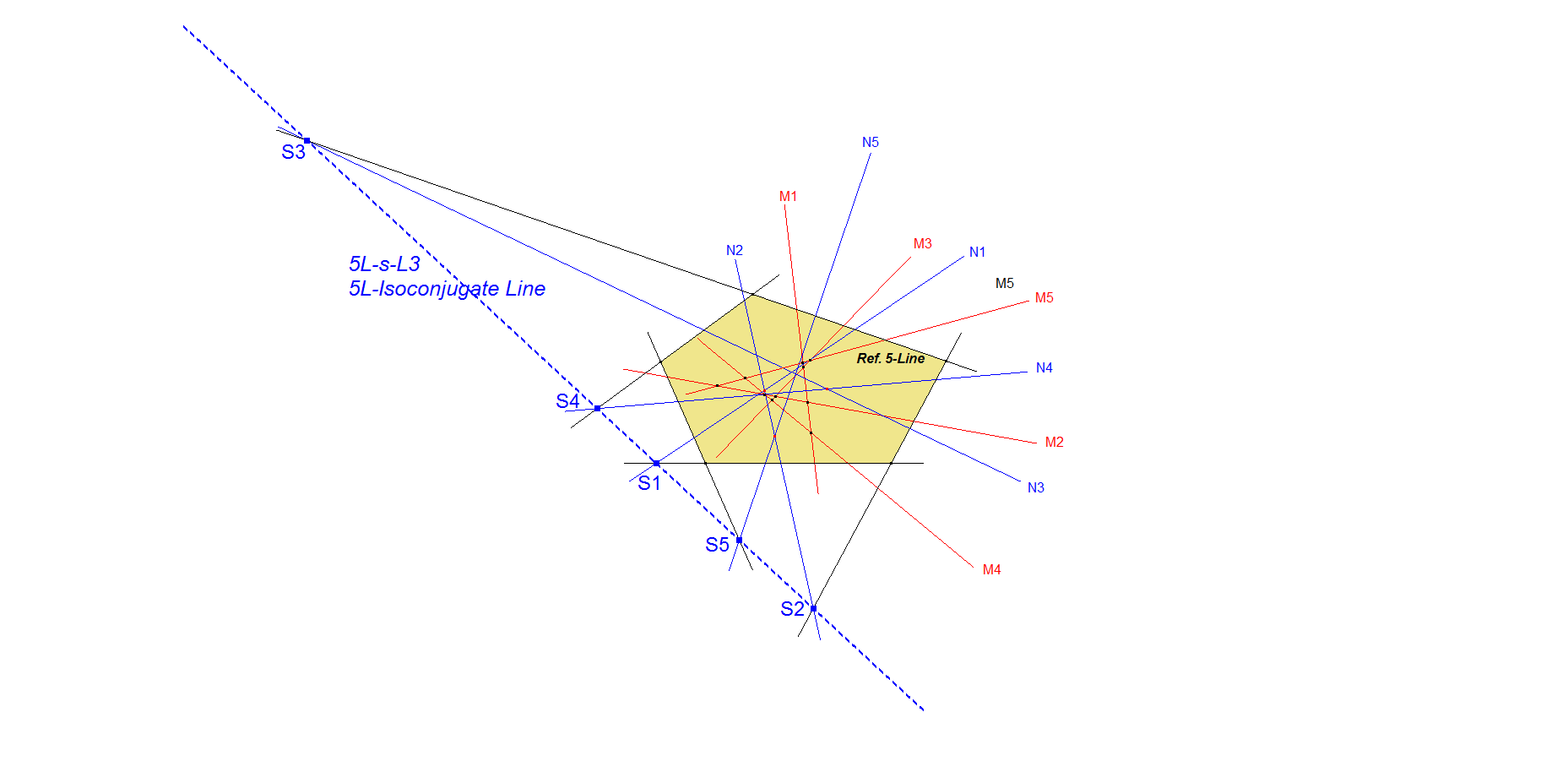
A 5-Line contains 5 Component Quadrilaterals / Component 4-Lines. When using a Component 4-Line one Line is not used or “omitted”.
Let Mi = QL-Tf2(Li), where Li is the omitted line for i=1,2,3,4,5.
In this way a new 5-Line M1.M2.M3.M4.M5 is created.
We can do the same procedure one level deeper,
Let Ni = QL-Tf2(Mi), where Mi is the omitted line for i=1,2,3,4,5.
In this way a new 5-Line N1.N2.N3.N4.N5 is created.
Now the 5 intersections of lines Li and Ni will be collinear on 5L-s-L2.
Summarized:
By applying the QL-Tf2 transformation (Isoconjugation for Lines) twice a 2nd level 5-Line is created.
The intersection points of corresponding lines of the reference 5-Line and the 2nd level 5-Line will be collinear on 5L-s-L2.
This is the dual case of 5P-s-P2.
See [34], QFG#784.
Properties
- 5L-s-L2 is tangent to a conic mentioned at 5L-s-P11.
Estimated human page views: 301
