5L-s-P2: 5L-X(186)-Hofstadter Point
The X(186)-circles of the 4-Lines (described at QL-P28: Circumcenter QL-X(186)-Quadrangle) applied in the 5-Line have one point in common (See [34], QFG#82, Seiichi Kirikami).
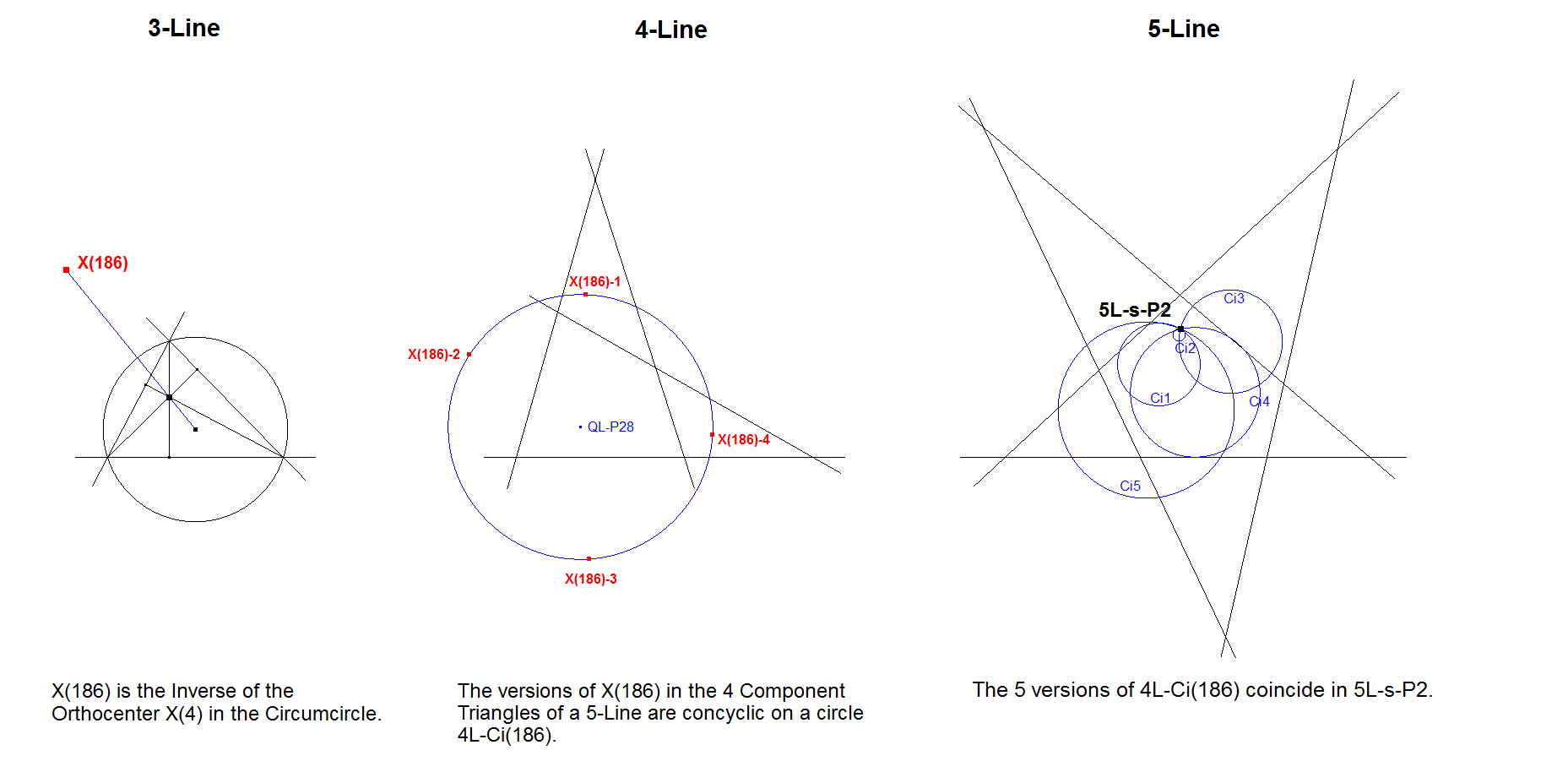
This sequence of Point –> Circle –> Common-point is typical for Hofstadter Triangle Points H(n) for n = integer <> -1, 0, +1. See remarks below.
Properties
- The same procedure exists for X(3), which also is a Hofstadter Point in a 3-Line. In a 4-Line the X(3)-versions are concyclic on 4L-n-Ci1 and the 5 versions of this circle in a 5-Line concur in 5L-n-P1. However this sequel continues infinitely for n>5, which is not the case for X(186).
- 5L-s-P2 lies on the Centercircle of the 5-Line 5L-n-Ci1. See nL-n-Ci1.
- 5L-s-P2 lies on the circle determined by the 5 QL-Tf1 images (wrt the component QL’s) of 5L-s-P3. See [34], Eckart Schmidt, QFG-message#2707.
Hofstadter Triangle Points
In the beginning of the 1990’s Prof. Doug Hofstadter observed a special type of triangle point.
A description of these points can be found at Ref-58, Clark Kimberling, “Hofstadter points,” Nieuw Archief voor Wiskunde 12 (1994) 109-114.
Hofstadter points also are defined in ETC (See Ref-12) at the preamble of X(360):
Let r denote a real number, but not 0 or 1. Using vertex B as a pivot, swing line BC toward vertex A through angle rB and swing line BC about C through angle rC. Let A(r) be the point in which the two swung lines meet. Obtain B(r) and C(r) cyclically. Triangle A(r)B(r)C(r) is the r-Hofstadter triangle; its perspector with ABC is called the Hofstadter H(r) point.
A subset of these points being the n-Angle Centers are defined by Ngo Quang Duong in [34], QFG#1843:
Pn is “n-angle center” of triangle ABC if (PB,PC)=n(AB,AC)(mod pi); (PC,PA)=n(BC,BA)(mod pi) then of course we have (PA,PB)=n(CA,CB)(mod pi).
Hofstadter points H(r) are defined for r=real number.
n-Angle Centers P(n) are points defined for n=integer <> 0 and 1.
It appears that the n-Angle Centers P(n) match with the Hofstadter points H(n) provided that n = integer <> 0 and 1.
For another summary and extra properties of these points see QL-P-1 and [34], QFG#1872.
Finally following n-Angle Centers 3L-P(n) are relevant in a 5-Line:
- etc.
- 3L-P(-4) = X(5964)
- 3L-P(-3) = X(5962)
- 3L-P(-2) = X(265)
- 3L-P(-1) = X(4)
- 3L-P(0) = undefined
- 3L-P(+1) = undefined
- 3L-P(+2) = X(3)
- 3L-P(+3) = X(186)
- 3L-P(+4) = X(5961)
- 3L-P(+5) = X(5963)
- etc.
Most important is that the n-Angle Centers 3L-P(n) for n<>-1,0,1 have in common that:
- In a 4-Line the 4 versions of 3L-P(n) of the Component Triangles are concyclic on a circle 4L-Ci(n) with Center 4L-P(n).
- In a 5-Line the 5 versions of 4L-Ci(n) of the Component 4-Lines concur in a point 5L-P(n).
The properties of this subset of the Hofstadter Points were gradually discovered in discussions at the Quadri-Forum ([34]) in 2013-2015 by Seiichi Kirikami, Chris van Tienhoven, Ngo Quang Duong, Tsihong Lau, Eckart Schmidt and Bernard Keizer.
It is fair to say that to date no exact proof has been found for the existence of 4L-Ci(n), 4L-P(n) and 5L-P(n) relating to the Hofstadter Points 3L-P(n), though several drawings confirm the validity of the mentioned conjectured properties.
Correspondence with ETC/EQF/EPG
|
Estimated human page views: 329
