8L-s-L1: 8L-Keizer-Schmidt Line
The Keizer-Schmidt Line 8L-s-L1 in an 8-Line (Octalateral) is the equivalent of the 8P-Cayley Bacharach Point 8P-s-P1 in an 8-Point (Octangle).
It was developed by Eckart Schmidt and Bernard Keizer during an extensive discussion at the Quadri-Figures-Group. See [34], search for keyword “ninth” to find the involved messages and especially messages #2511, #2513, #2515-#2519, #2561, #2640, #2641, #2644, #2662, #2663, #2677, #2678, #2679, #2691, #2693.
It is defined as follows:
Let L1,…,L8 be eight distinct lines in the plane, no four of which concurrent, and no seven of them tangent to a conic. There exists a unique ninth line L9 such that every curve of class 3 tangent to L1, …..,L8, also will be tangent to L9.
Degree vs. Class of an algebraic curve
Note that in the Cayley-Bacharach Theorem for 8 points delivering a ninth point, these points lie on a curve of degree 3. However in the equivalent for 8 lines delivering a ninth line, these points are tangent to a curve of class 3.
The degree of an algebraic curve Cv may be defined as the number of intersection points that can be found when intersecting Cv with a line (counting multiplicities and including imaginary points).
The class of an algebraic curve Cv may be defined as the number of tangents that may be drawn to Cv from a point not on Cv (counting multiplicities and including imaginary tangents).
Construction
8L-s-L1 is proposed and constructed by Eckart Schmidt as follows:
Consider eight lines and take four for a reference QL and its dual QA,
… duality gives eight points for the eight lines,
… take their Cayley-Bacharach ninth point,
… its dual will give the Cayley-Bacharach ninth line.
The construction is independent of the chosen reference QL!!!
See [34], QFG#2511, QFG#2662.
The mentioned QL-duals are line-point-dual QL-Tf10 and point-line-dual QL-Tf11.
The mentioned Cayley-Bacharach ninth point is 8P-s-P1.
Example
The eight angle bisectors of a Quadrigon (4-Gon) have a Cayley-Bacharach ninth line 8L-s-L1.
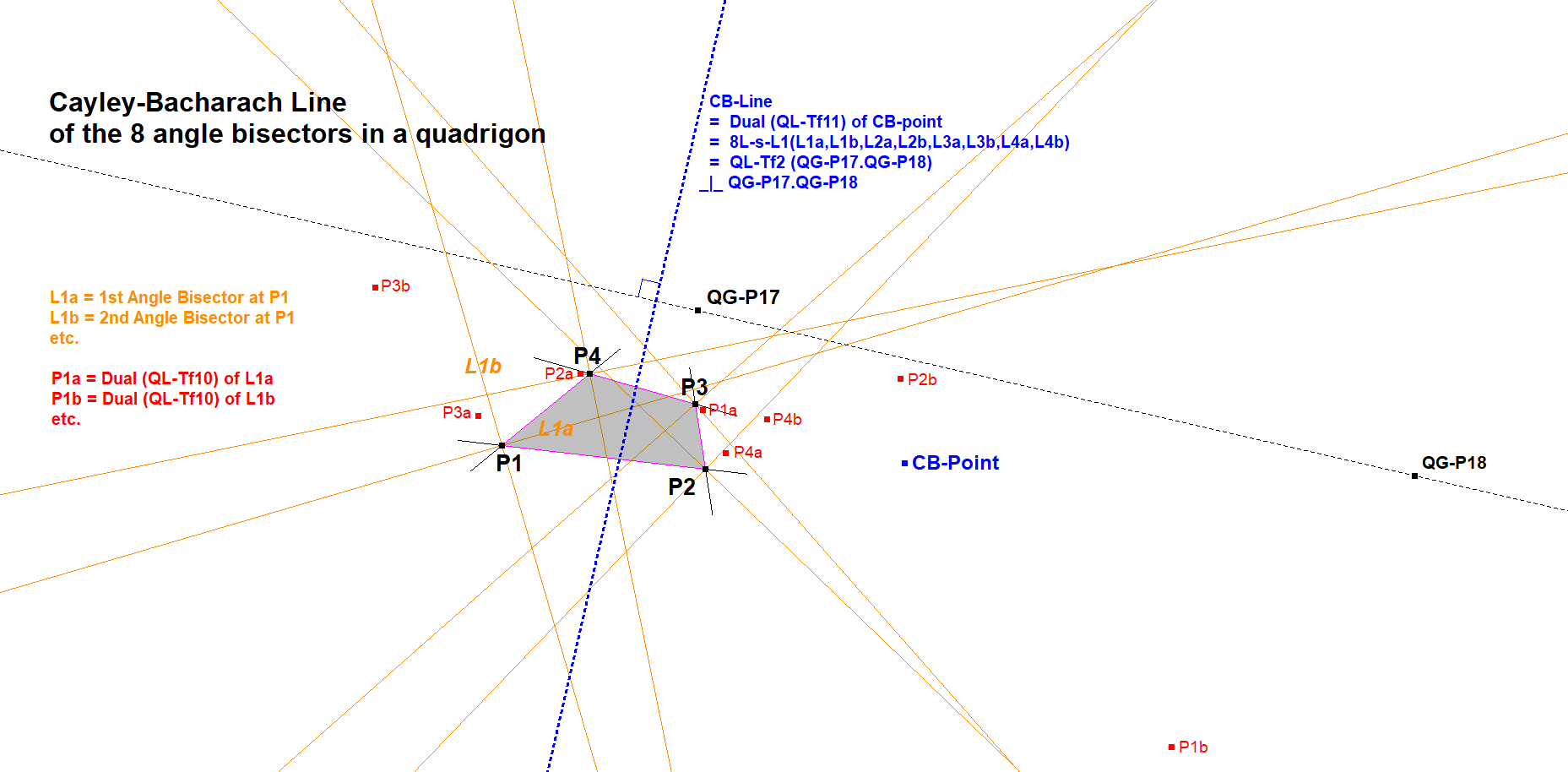
In this case the curve of class 3 is not clear, but when we consider mentioned 8 lines to be tangent to some curve of class 3, then the ninth line 8L-s-L1 always will be tangent too.
Special properties for this configuration
- The QL-Tf2-image of QG-P17.QG-P18 is the ninth CB-line wrt the eight angle bisectors of a Quadrigon.
- The 3 CB-lines of the Component Quadrigons of a Quadrilateral have a common point.
- This common point has 1st DT-coordinate: m2 n2 SA2(l2 SB SC a2 + m2 SC S2 + n2 SB S2).
See [34], Eckart Schmidt, QFG#2677.
Estimated human page views: 325
