nL-e-L1: nL-Morley’s Ortho Directrix
This line is described in Ref-49, Morley’s paper: Orthocentric properties of the Plane n-line.
There is no nL-first Orthocenter for n=even but there are n (n-1)L-first Orthocenters (since an n-Line contains n (n-1)-Lines). They will be collinear on the so called nL-Morley’s Ortho directrix.
When n=4, then QL-L2 (Steiner Line) will be the 4L-Morley’s Ortho directrix, containing the Orthocenters X(4) of the 4 Component triangles.
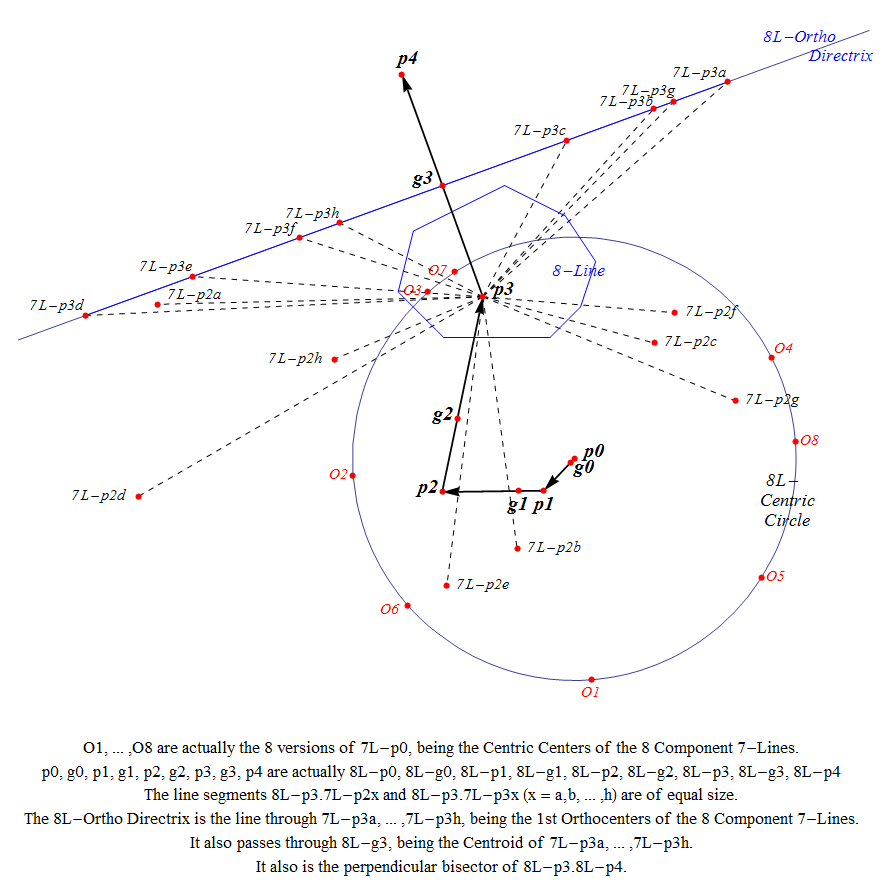
Example Morley’s Ortho directrix in an 8-Line
The sides of the blue 8-Gon represent the basic lines of the 8-Line.
8L-n-p3 (p3 in the picture) is Morley’s 1st orthocenter of the 8-Line.
It is constructed via g0 to p1 (1:8), via g1 to p2 (2:8), via g2 to p3 (3:8) , via g3 to p4 (4:8), where:
- g0 = centroid of 8 points 7L-n-p0
- g1 = centroid of 8 points 7L-n-p1
- g2 = centroid of 8 points 7L-n-p2
- g3 = centroid of 8 points 7L-n-p3.
In this picture where n=even one of the pi has a prominent place: 8L-n-p3, which also is the common point of the perpendicular bisectors of all component 7-Line segments 7L-n-p2.7L-n-p3.
In general when n=even, then nL-n-p(n-1)=Center of the inscribed EnnaDeltoid. See Ref-49, §4.
Correspondence with ETC/EQF
When n=4, then nL-e-L1 = QL-L2 (Steiner Line).
Properties
- nL-e-L1 is the Perpendicular Bisector of nL-n-p((n-2)/2) and nL-n-p(n/2)). See nL-n-pi.
Estimated human page views: 312
