nL-n-Luc5 nL-Ref/Per/Par constructions
nL–n–Luc5 is referred to as a Level-up construction because, under specific conditions, it transforms a Central Point of an n-Line into a Central Point of an (n+1)-Line.
nL–n–Luc5 represents a class of constructions that will be further subdivided.
It transforms an n-Line into another n-Line by drawing lines through the n versions of a given Central Point (denoted (n–1)–Px), either perpendicular or parallel to the omitted line.
The reference n-Line is called Ref.
- When parallel lines are drawn through the n versions of (n–1)–Px, the resulting n-Line is called Par. If multiple generations are constructed, the resulting n-Lines are denoted Par1, Par2, etc.
- When perpendicular lines are drawn through the n versions of (n–1)–Px, the resulting n-Line is called Per. If multiple generations are constructed, the resulting n-Lines are denoted Per1, Per2, etc.
When any pair from the set {Ref, Par1, Par2, Per1, Per2} are perspective, a Perspective Center is formed, denoted XXX/YYY–PC(Px), where XXX and YYY are distinct names from the group.
If the corresponding lines of XXX and YYY are parallel and the pair is also perspective, the resulting center is called a Homothetic Center, denoted XXX/YYY–HC(Px).
Further Details
Every n-Line consists of n component (n–1)-Lines, each constructed by omitting one line from the original n-Line.
- By drawing parallels to the omitted line through the n (n–1)L versions of a central point, a new n-Line is formed, called Par1.
- Repeating this process with Par1 as the reference n-Line yields a second-generation n-Line, Par2.
- Similarly, drawing perpendiculars to the omitted line through the (n–1)L versions of a central point produces Per1.
- Repeating this with Per1 as the reference n-Line yields Per2.
Various combinations of Ref, Par1, Par2, Per1, and Per2 may exhibit homothetic or perspective relationships, giving rise to corresponding Homothetic Centers (HC) or Perspective Centers (PC).
Examples
Although most of the times there will no perspectivity there are plenty of positive examples:
- nL-n-P5 applied in n (n-1)-Lines gives homothetic Ref / Par1, creating nL-n-P2.
- X(4) applied in 4 3-Lines gives a Ref/Par1-HC, being QL-P20.
- X(4) applied in 4 3-Lines gives a Par1/Per1-PC, being QL-P21.
- 5L-s-P1 applied in 6 5-Lines gives a Ref/Par2-HC, being 6L-s-P2.
- 5L-s-P1 applied in 6 5-Lines gives a Ref/Per2-HC, being 6L-s-P3.
- 5L-s-P1 applied in 6 5-Lines gives a Par2/Per2-HC, being 6L-s-P4.
- etc.
Not always a Perspective Axis
Note that although there is a Perspective Center/Homothetic Center of two n-Lines for n>3 there not always is a Perspective Axis. Actually there mostly is no Perspective Axis. There is a Perspective Axis when the intersection points of corresponding lines are collinear on a Perspective Axis.
A nice example is the Perspective Axis of Par1/Per1-Perspective Center QL-P21, being the Steiner Line QL-L2.
Present state of research
There is a huge differentiation in perspective pairs of n-Lines coming from (Ref, Per1, Per2, Per3, Per4, Par1, Par2, Par3, Par4).
Most common are the perspectivities of these pairs of n-Lines:
- Ref/Par1 (consequently also Par1/Par2, etc.)
- Par1/Par2 (without perspectivity of Ref/Par1)
- Ref/Per2
- Par1/Per2
But it has to be said that most of the times there will be no homothetic / perspective pair of n-Lines.
So each occurrence of a Ref-Per-Par-perspectivity for some Px is special.
Examples ETC-points applied in a 4-Line
X(2) in a 4-Line
Perspective/Homothetic Centers:
- Ref/Par1 = QL-P12
- Ref/Per2 = Ref/Per4 = Per1/Per3 = Per2/Per4 = QL-Px = Midpoint QL-P5 . QL-P29 = Midpoint QL-P2 . QL-P20 = Reflection of QL-P6 in QL-P22
- Par1/Per2 = QL-P12 . QL-Px (4:1)
- Par1/Per4 = QL-P12 . QL-Px (40:1)
These 4 Perspective/Homothetic Centers are collinear.
X(4) in a 4-Line
Note: Ref=Par2=Par4, Par1=Par3
Perspective/Homothetic Centers:
- Ref/Par1 = QL-P20
- Ref/Per2 = InfinityPoint (QL-P2 . QL-P20)
- Par1/Per1 = QL-P21
- Par1/Per2 = QL-P2 . QL-P20 (-1:2)
nL-n-Luc5a nL-Ref/Par1 construction
nL-n-Luc5a is a Level-up construction which uses the Reference n-Line Ref and the 1st generation parallel n-Line Par1 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
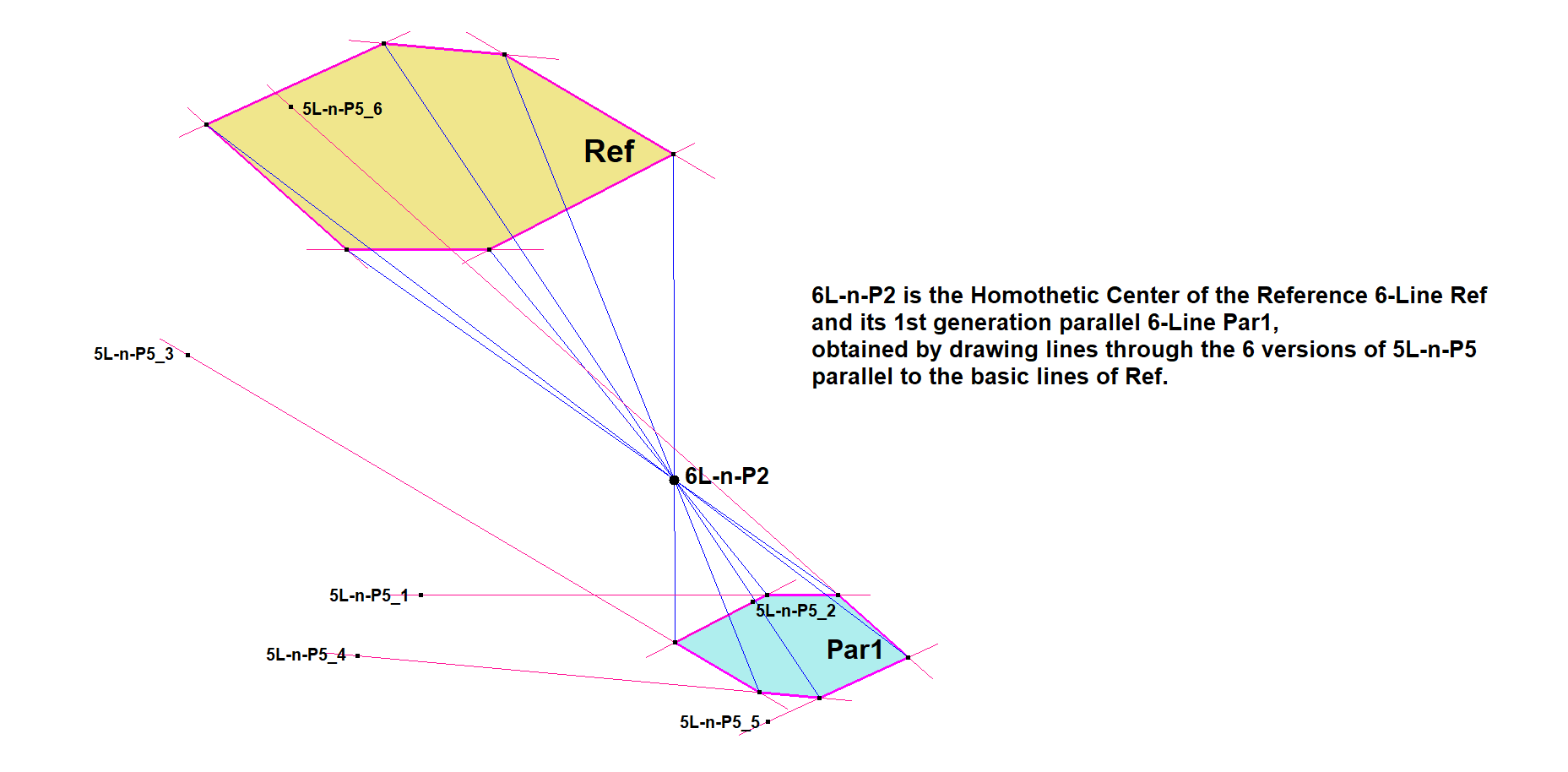
Examples
| 3L-point | 4L-point | 5L-point | 6L-point | higher |
|---|---|---|---|---|
| 3L-n-P8= X(2) | 4L-n-P8= QL-P12(Ref/Par1-HC, Ref=Par2) | 5L-n-P8 (Ref/Par1/Par2-HC) | 6L-n-P8 (Ref/Par1/Par2-HC) | Etc. |
| 3L-n-P3 /P9= X(3) | 4L-n-Px= QL-P5(Ref/Par1-HC, Ref=Par2) | No Ref/Par1-relationship.
No Ref/Par2-relationship. No Par1/Par2-relationship. |
— | — |
| 3L-n-P4 /P10= X(4) | 4L-n-Px= QL-P20(Ref/Par1-HC, Ref=Par2) | 5L-s-P7 (Par1/Par2-HC)
No Ref/Par1-relationship. No Ref/Par2-relationship. |
No Ref/Par1-relationship.
No Ref/Par2-relationship. No Par1/Par2-relationship. |
— |
| 3L-n-P5 /P11= X(5) | 4L-n-P2= QL-P22(Ref/Par1-HC, Ref=Par2) | No Ref/Par1-relationship.
No Ref/Par2-relationship. No Par1/Par2-relationship. |
— | — |
| Points on line 5L-n-P8.5L-n-P2preserving distance ratio’s(Ref/Par1/Par2-HC) | No Ref/Par1-relationship.
No Ref/Par2-relationship. No Par1/Par2-relationship. |
— |
Note that the mutual distance ratios of points X(2), X(3), X(4), X(5) (lying on the 3L-Eulerline) and resp. of QL-P12, QL-P5, QL-P20, QL-P22 (lying on the 4L-Newton Line) are identical.
Summary
General cases
- nL-n-Luc5a (nL-n-P8) = pL-n-P8, where p=(n+1)
- nL-n-Luc5a (nL-n-P5) = pL-n-P2, where p=(n+1)
- nL-n-Luc5a (nL-n-Px) = pL-n-Py, where p=(n+1) and
- nL-n-Px = Ratiopoint nL-n-P8 . nL-n-P5 (s:t)
- pL-n-Py = Ratiopoint pL-n-P8 . pL-n-P2 (s:t),
- meaning that the line nL-n-P8 . nL-n-P5 is leveled-up into the line pL-n-P8.pL-n-P2
- and that distance ratios are preserved.
Specific cases
- nL-n-Luc5a (X(3)) = QL-P5, there is no nL-n-Luc5a (QL-P5)
- nL-n-Luc5a (X(4)) = QL-P20, there is no nL-n-Luc5a (QL-P20)
- nL-n-Luc5a (X(5)) = QL-P22, there is no nL-n-Luc5a (QL-P22)
nL-n-Luc5b nL-Ref/Par2-Construction
nL-n-Luc5b is a Level-up construction which uses the Reference n-Line Ref and the 2nd generation parallel n-Line Par2 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
When Par1 is homothetic with Ref, consequently also Par2 will be homothetic with Par1. We have actually a Ref/Par1/Par2 relationship. However it is possible that Par1 is not homothetic or even perspective with Ref, whilst Par2 still is.
There are no examples of this level-up construction found yet, but in principle their existence should be possible.
nL-n-Luc5c nL-Ref/Per1-Construction
nL-n-Luc5c is a Level-up construction which uses the Reference n-Line Ref and the 1st generation perpendicular n-Line Per1 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
There are no examples of this level-up construction found yet, but in principle their existence should be possible.
nL-n-Luc5d nL-Ref/Per2 constructions
There are indications that the Ref/Per2 Construction applies for all ETC-points.
After checking several different ETC-points it appeared that all these ETC-points could be Ref-Per2 transformed into 4L-points. See [34], QFG#1937.
There is no indication that all these 4L-points are Ref/Per2-transferable into 5L-points.
Let X(r) be a point on the 3L-Euler line dividing X(3).X(4) with ratio r, then the Ref-Per2-transformed point will be a point on the line QL-P2.QL-P20.
Other collinear 3L-ETC-points were transformed into 4L-points on a conic.
Possibly it is a transformation of the 2nd degree. See [34], QFG#1938.
Enough indications for further research.
Ref/Per2-HC constructions
| 3L-point | 4L-point | 5L-point | 6L-point | higher |
|---|---|---|---|---|
| 3L-n-P2 / P8= X(2) | 4L-n-Px= Midpoint (QL-P2.QL-P20) | No new Ref/Per2-HC | — | — |
| 3L-n-P3 / P9= X(3) | Ref = Per2→ Indefinite result | Indefinite Ref/Per2-HC | — | — |
| 3L-n-P4 / P10= X(4) | 4L-n-Px= InfinityPoint (QL-P2.QL-P20) | Indefinite Ref/Per2-HC | — | — |
| 3L-n-P5 / P11= X(5) | Per1 = QL-P2→ Indefinite result | Indefinite Ref/Per2-HC | — | — |
| 4L-n-P8 = QL-P12 | ||||
| 4L-n-P5 = QL-P30 | 5L-n-P8 |
nL-n-Luc5e nL-Par1/Par2 constructions
nL-n-Luc5e transforms a point (n-1)L-n-Px into a similar point nL-n-Px by drawing lines through the n versions of (n-1)L-n-Px in a reference n-Line parallel to the omitted line.
- Suppose the reference n-Line is called Ref.
- When drawing parallel lines through the n versions of (n-1)L-n-Px the result will be an n-Line called Par1.
- When drawing another generation (acting like Par1 is Ref) the resulting n-Line will be called Par2.
- When the corresponding lines of Par1 and Par2 are parallel and Par1 and Par2 are perspective, then this Perspective Center will be called Homothetic Center Par1/Par2-HC(nL-n-Pi)).
Par1/Par2-Level-up constructions on nL-n-Px
It appears that :
- nL-n-Luc5e (3L-n-Pi) = 4L-n-Pi for i = 1,…,11
- nL-n-Luc5e (nL-n-P8) = (n+1)L-n-P8 for n = 4,5,6,7,8,9, . . .
- nL-n-Luc5e (nL-n-P3) exists for n = 4,5,6,7 (then possible end of homothecy)
- nL-n-Luc5e (nL-n-P5) exists for n = 4,5,6 (then possible end of homothecy)
- nL-n-Luc5e (nL-n-P7) exists for n = 4,5,6,7,8 (9 gives calculation problems)
Examples
CC(H(i)) = Center of the 4L-Centercircle wrt HofstadterPoint(i).
Par1/Par2 constructions on nL-Hofstadter Points
- In a 5-Line starting with 4L- n-P13 (QL-P28) as Central Point for the Component 4-Lines it appears that 5L-Par1 is homothetic with 5L-Par2 giving a Homothetic Center 5L-n-P13.
- In a 6-Line starting with 5L- n-P13 as Central Point for the Component 5-Lines it appears that 6L-Par1 is homothetic with 6L-Par2 giving a Homothetic Center 6L- n-P13.
- In a 7-Line starting with 6L- n-P13 as Central Point for the Component 5-Lines it appears that 7L-Par1 is homothetic with 7L-Par2 giving a Homothetic Center 7L- n-P13.
- etc.
This process can be repeated for all other known QL-points generated from Hofstadter Points X(3), X(186), X(256), X(5961), X(5962), X(5963), X(5964).
Corresponding Central Points in the 4-Line will be QL-P4 (wrt X(3)), QL-P28 (wrt X(186)), QL-P29 (wrt X(256)).
I checked it graphically in Cabri for X(256) up to level n=6. Further drawings for n>6 were impossible because of the many internal calculations for the drawing software.
After verifying with Mathematica software, certain limitations were identified regarding the extensive internal calculations.
However there were no contra indications for:
- X(3)
- X(186) up to level n=8
- X(256) up to level n=7
- X(5961) up to level n=7
- X(5962) up to level n=7
- X(5963) up to level n=6
- X(5964) up to level n=4
Based on these findings, this conjecture appears sufficiently supported:
- Let 3L-P(i) be n-Angle Centers P(i) in a Triangle as described in QFG-message #1872, where i <> -1, 0, 1.
- Let 4L-Q(i) be the Circumcenter of the 4 versions of 3L-P(i) in a 4-Line.
- For these points nL-Par1 will be homothetic with nL-Par2 using (n-1)L-Q(i) as Central Point, producing new Homothetic Center nL-Q(i), for all n > 4.
nL-n-Luc5f nL-Par1/Per1-construction
nL-n-Luc5f is a Level-up construction which uses the 1st generation parallel n-Line Par1 and the 1st generation perpendicular n-Line Per1 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
Example QL-P21.
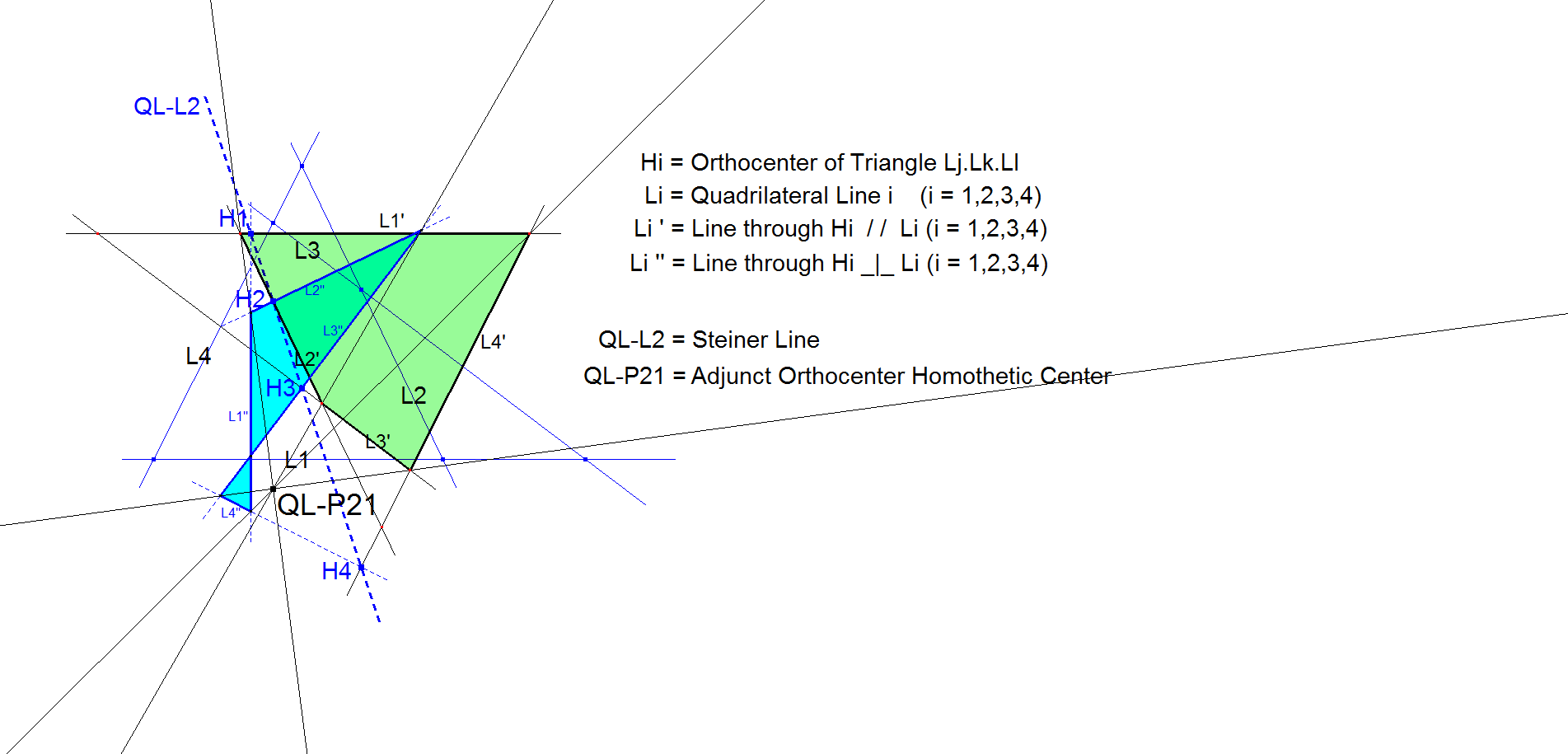
Note that QL-L2=Steiner line is the Perspective Axis of Par1/Per1.
nL-n-Luc5g nL-Par1/Per2-construction
nL-n-Luc5g is a Level-up construction which uses the 1st generation parallel n-Line Par1 and the 2nd generation perpendicular n-Line Per2 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
Examples are 5L-s-P9 and 5L-s-P10 and 5L-n-P12.
Also
nL-n-Luc4g (X(2)) = QL-P12 . Mid(QL-P2,QL-P20) (5:-1)
nL-n-Luc4g (X(4)) = QL-P20 . QL-P2 (2:-1).
nL-n-Luc5h nL-Par2/Per1-Construction
nL-n-Luc5h is a Level-up construction which uses 2nd generation parallel n-Line Par2 and the 1st generation perpendicular n-Line Per1 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
There are no examples of this level-up construction yet, but in principle their existence should be possible.
nL-n-Luc5i nL-Par2/Per2-construction
nL-n-Luc5i is a Level-up construction which uses the 2nd generation parallel n-Line Par2 and the 2nd generation perpendicular n-Line Per2 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
Examples are QL-P28 and QL-P29 used as lower-level-points in a 5-Line.
See pictures 5L-s-P9 and 5L-s-P10.
Possibly there are other incidences with related Hofstadter 4L-Points.
nL-n-Luc5j nL-Per1/Per2-Construction
nL-n-Luc5j is a Level-up construction which uses the 1st generation perpendicular n-Line Per1 and the 2nd generation perpendicular n-Line Per2 wrt some lower-level center to construct a Perspective / Homothetic Center. See nL-n-Luc5.
There are no examples of this level-up construction yet, but in principle their existence should be possible.
Estimated human page views: 481
