nL-n-pi: nL-Morley’s intermediate recursive pi points
nL-n-pi is a point defined by Morley in Ref-49.
Note that the letter “p” is in lower case. In Morley’s document it is denoted as “pi”.
Since it can occur in all n-Lines for n>1 it is named here nL-n-pi.
The existence of nL-n-pi as well as nL-n-gi are purely algebraically indicated by Morley.
Morley uses it as intermediate point(s) to make it possible to construct his so called first Orthocenter (nL-o-P1) as well as his so called Ortho Directrix (nL-e-L1).
nL-n-pi (i = 1, .. ,(n-1)/2) is defined in a recursive way:
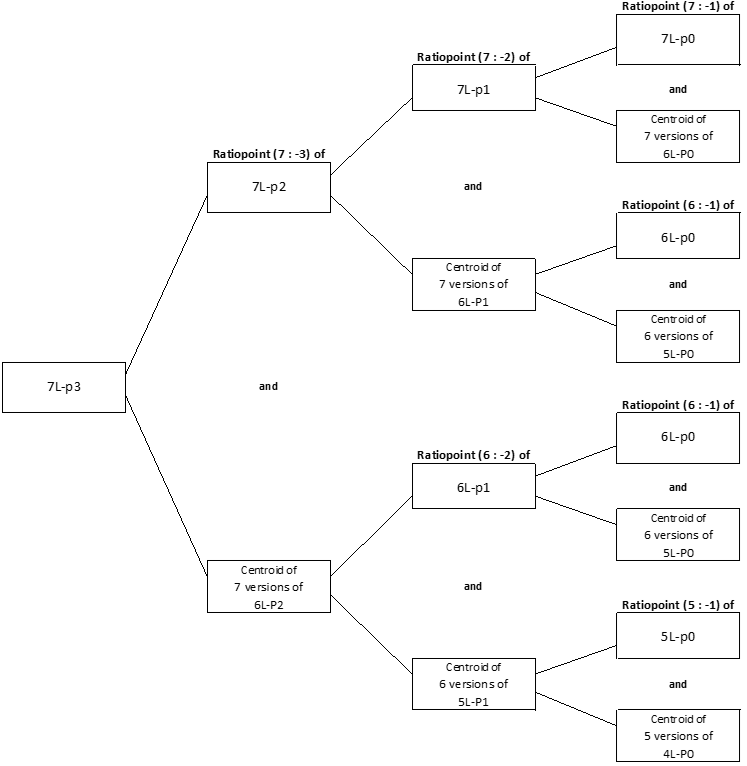
nL-n-pi = Ratiopoint of
nL-n-p(i-1) and
nL-n-g(i-1) being the centroid of n points (n-1)L-n-p(i-1)
with ratio n : (i-n).
By applying this formula to an increasingly lower level finally the level is reached unto some nL-n-p0, and nL-n-p0 is defined as follows:
nL-n-p0 = Center of the nL-Centric Circle of an n-Line, also called the nL-Centric Center being nL-n-P3.
The nL-Centric Center now in turn is defined as the center of the circle through the n (n-1)L-Centric Centers.
By applying this definition to an increasingly lower level finally the level is reached of the 3L-Centric Center, which simply is the center of the circumcircle of a triangle.
This is the only known item and can be rolled up (wherever it appears) to the required point nL-n-pi. Basically nL-n-pi is built from large quantities of triangle circumcenters. These triangles being formed by the different combinations of the basic lines of the n-Line.
Example
See nL-o-P1 (Morley’s first Orthocenter) for examples of the use of nL-n-p1.
The first two points for i=0,1 are well known points:
Behavior nL-n-pi points for different values of i
1. These properties are valid for Morley’s nL-pi points when n = odd (denote mL = (n-1)L):
- nL-n-pi has a fixed distance ratio with the n versions of mL-n-pi & mL-n-p(i-1), when i=0, … , (n+1)/2, but not for higher values.
- For n > 5 there are two orthogonal reflective axes for i=(n-1)/2, bisecting angles with lower level mL-n-pi.X.mL-n-p(i-1), where X=nL-o-P1 and m=(n-1). See : nL-o-2L1.
- nL-n-pi for i = 0,1,2,3, … ,n culminates in a point nL-n-pn, which will be the same point as the centroid of the n lower level points mL-n-p(n-1). That is because, when i=n then nL-g(n-1) =nL-n-pn (Ratiopoint (n:0)).
- When i > n the outcome will produce the same point nL-n-pn because the end of iteration has been reached.
2. These properties are valid for nL-pi points when n = even (denote mL = (n-1)L):
- nL-n-pi has a fixed distance ratio with the n versions of mL-n-pi & mL-n-p(i-1), when i=0, … , n/2, but not for higher values. This distance ratio =1, when i = n/2 – 1. As a consequence nL-n-p(n/2-1) will be the common point of the perpendicular bisectors of the n pairs mL-n-p(n/2-1), mL-n-p(n/2-2).
- When n=even there are no orthogonal reflective axes at any nL-pi bisecting angles with lower level mL-n-pi and mL-n-p(i-1).
- nL-n-pi for i = 0,1,2,3, … ,n culminates in a point nL-n-pn, which will be the same point as the centroid of the lower level points mL-n-p(n-1). That is because, when i=n then nL-g(n-1) =nL-n-pn (Ratiopoint (n:0)).
- When i > n the outcome will produce the same point nL-n-pn because the end of iteration has been reached.
In general:
- nL-n-p0 = nL-n-P3 = nL-Center Circle Center
- nL-n-p1 = nL-n-P7 = nL-Hervey Point
- for n=odd: nL-n-p((n-1)/2) = nL-o-P1 = nL-Morley’s 1st Orthocenter
- for n=even: nL-n-p((n/2)-1) = nL-e-P1 = nL-Morley’s EnnaDeltoid Center
See also the notes at nL-n-gi.
Correspondence with ETC/EQF
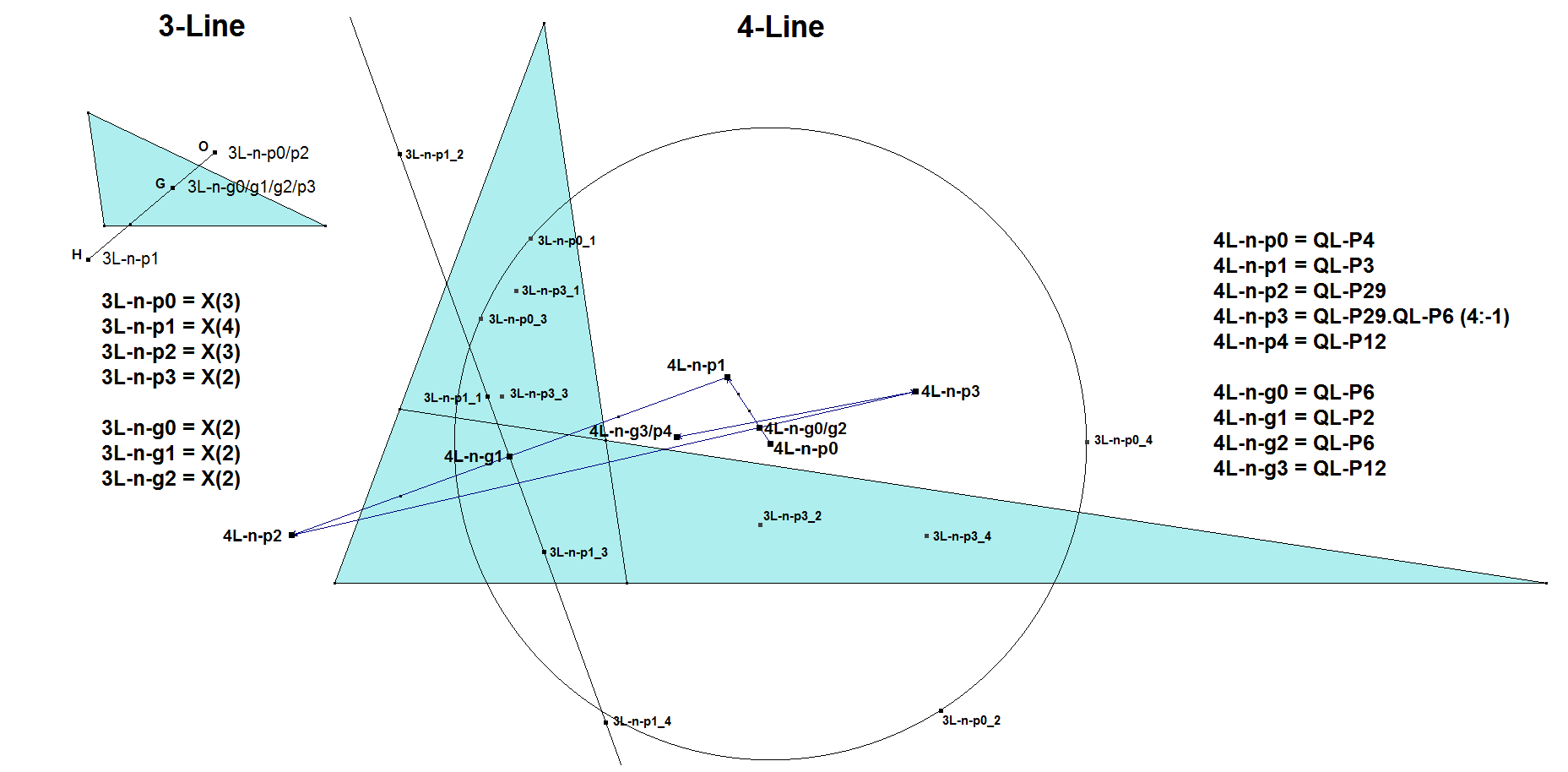
- When n=3, then:
- 3L-n-p0 = X(3)
- 3L-n-p1 = X(4)
- 3L-n-p2 = X(3)
- 3L-n-p3 = X(2)
- When n=4, then:
Behavior of nL-n-pi and nL-n-gi in a 3-Line and a 4-Line
(using that in a 2-Line every outcome of 2L-n-pi=2L-n-gi=L1^L2)
Behavior of nL-n-pi and nL-n-gi in a 5-Line
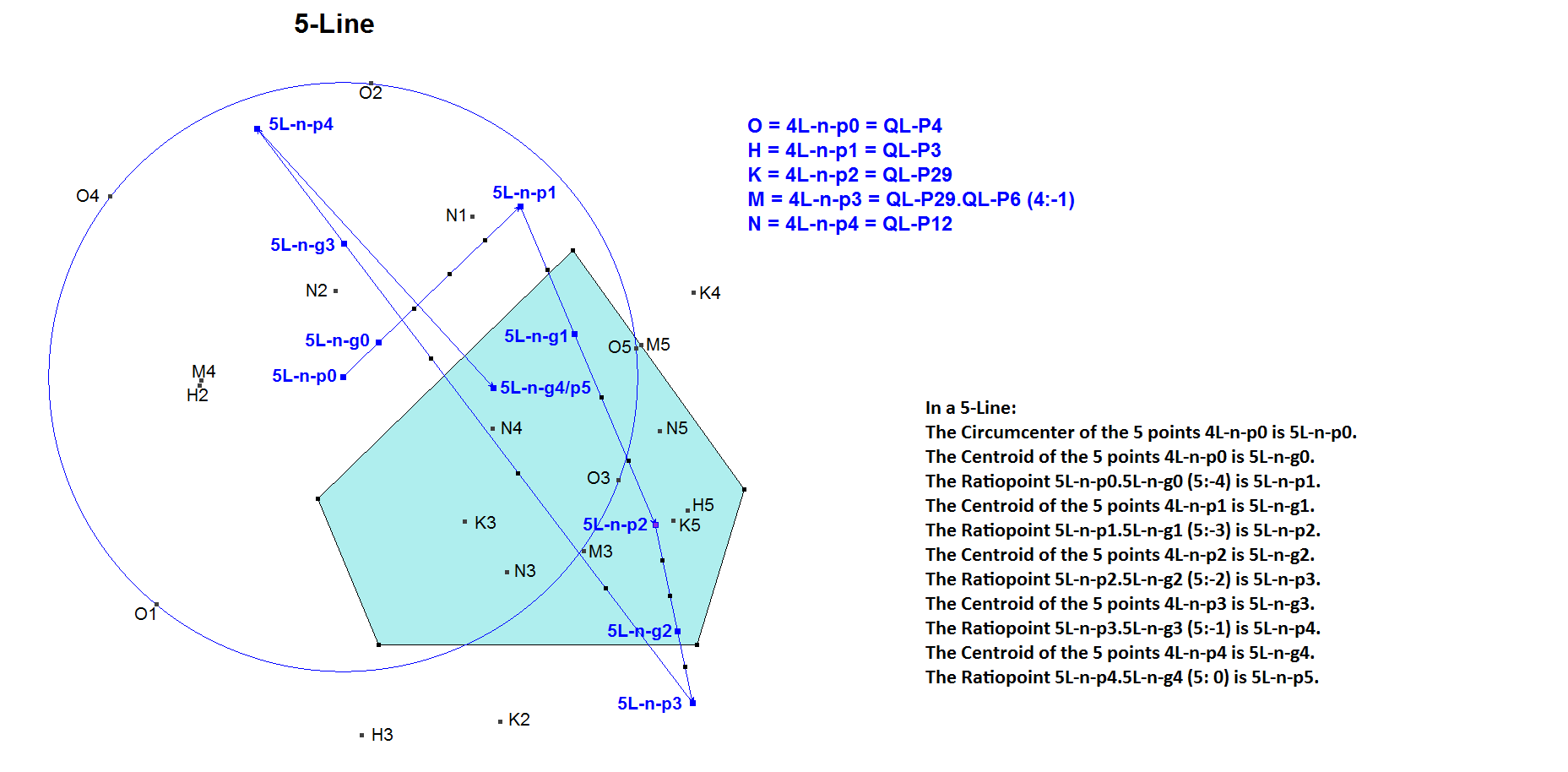
Note that the results of the lower levels are used in the higher levels.
The results of nL-n-pi are shown for i=1, … ,n, although they are used for lower values of i:
- in odd cases nL-o-P1 = nL-n-pi for i = (n-1)/2, and
- in even cases nL-n-P1 = nL-n-pi for i = (n/2) -1 .
Estimated human page views: 311
