nL-o-P1: nL-Morley’s 1st Orthocenter
Morley describes a so called first Orthocenter in his document “Orthocentric properties of the plane n-Line” (Ref-49). Morley’s paper was published in the year 1902. Morley proofs all his results algebraically using calculations in the complex plane. He explains his methods at Ref-48.
See also [34], QFG-messages #910, #912, #913, #917.
In Morley’s description he describes a recursive method of constructing this point, using intermediate points pi, where ‘i’ is a number in the range 0, … , (n-1)/2 (note that the letter “p” is in lower case).
Ultimately pi, when ‘i’ has reached the value (n-1)/2, then it is Morley’s 1st Orthocenter.
Morley’s 1st Orthocenter in a 3-Line is X(4), the triangle orthocenter.
In general Morley’s 1st Orthocenter in an n-Line (n=odd) is nL-n-pi, where i=(n-1)/2.
In a 3-Line Morley’s 1st Orthocenter will be 3L-n-p1, in a 5-Line it will be 5L-n-p2, in a 7-Line it will be 7L-n-p3, etc. (see nL-n-pi).
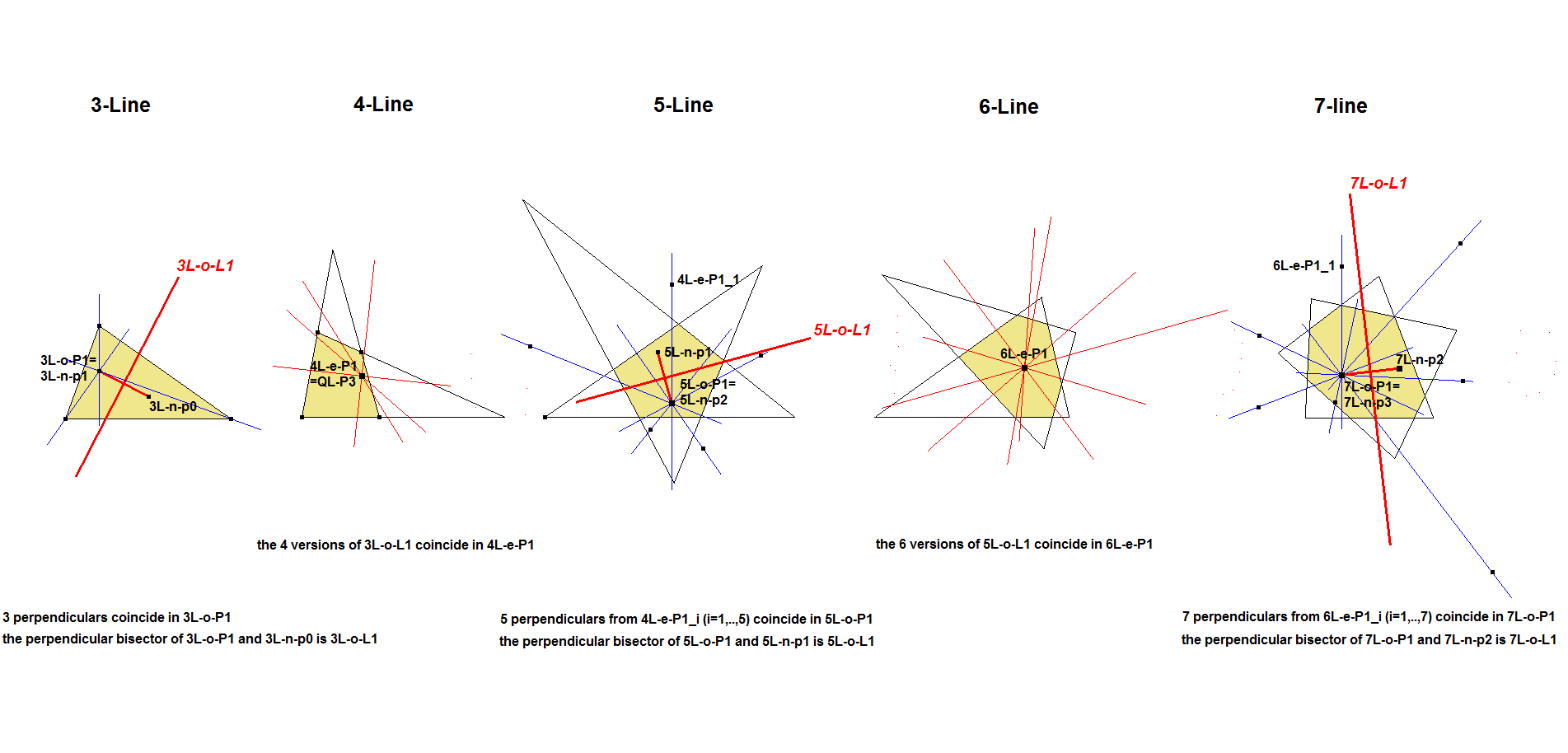
There is also a chain of constructing nL-o-P1 and nL-e-P1 in subsequent alternating odd and even n-Lines:
Other Properties
To prevent many abstract notations properties in a 9-Line will be mentioned. The general principle works accordingly. Intermediate points nL-n-pi will be mentioned (note that the letter “p” is in lower case).
- Morley’s 1st Orthocenters applied for all 10 Component 9-Lines in a 10-Line will be collinear on the so called 10L-Morley’s Ortho directrix.
- Morley’s 1st Orthocenter is the common point of the perpendiculars of 8L-n-p3 on the omitted line (by regularly omitting a line there are 9 component 8-Lines in a 9-Line).
- Using 9L-n-p4 as origin, the segments 9L-n-p4.8L-n-p4 and 9L-n-p4.8L-n-p3 have a fixed ratio for all 9 occurrences of 8L-n-p4 and 8L-n-p3. In general this property is also valid using lower 9L-level points 9L-n-p3, 9L-n-p2, 9L-n-p1 as origin and connecting them with their lower 8L-level points.
- There are two orthogonal axes (nL-2oL1) at Morley’s first Orthocenter X bisecting the 9 versions of angles 8L-n-p3.X.8L-n-p4. In general this property is only valid for n=odd>5 and angles L-n-pi.X.mL-n-pj, where m=(n-1), i=(m-2)/2, j=m/2.
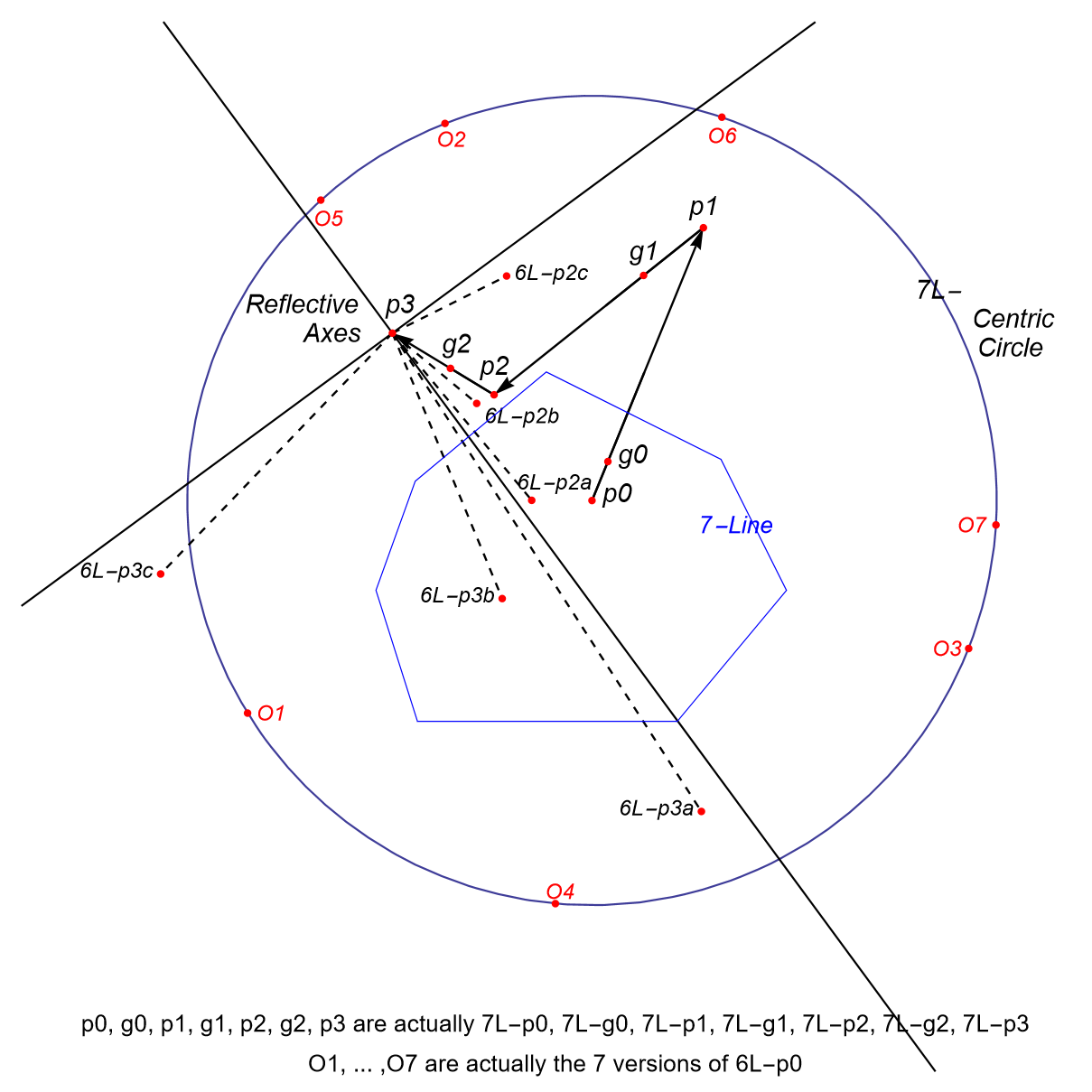
Example Morley’s first Orthocenter in a 7-Line
The sides of the blue 7-Gon represent the basic lines of the 7-Line.
7L-n-p3 (p3 in the picture) is Morley’s 1st orthocenter of the 7-Line.
It is constructed via g0 to p1 (1:7), via g1 to p2 (2:7), via g2 to p3 (3:7), where:
- g0 = centroid of 7 points 6L-n-p0
- g1 = centroid of 7 points 6L-n-p1
- g2 = centroid of 7 points 6L-n-p2
Only three of the seven 6L-n-p3i points and 6L-n-p2i points have been drawn for checking the fixed relationship of distances 7L-n-p3 unto 6L-n-p3i and 6L-n-p2i.
In this picture 7L-n-p3.6L-n-p3x : 7L-n-p3.6L-n-p2x = 2.6167 for all x, where x=a,b,c, . . . (total 7).
Correspondence with ETC/EQF
- When n=3, then nL-o-P1 = X(4).
Properties
- Morley’s 1st Orthocenter nL-o-P1 is the common point of the perpendiculars of all lower level (n-1)L-e-P1 to the omitted line (Level-up Construction nL-n-Luc1).
- Morley’s 1st Orthocenters applied for all (n+1) Component n-Lines in a (n+1)-Line will be collinear on the so called (n+1)L-Morley’s Ortho Directrix (n+1)L-e-L1.
- When n=odd using nL-o-P1 as origin, the segments nL-o-P1.mL-n-p((n-1)/2) and nL-o-P1.mL-n-p((n/2)-1) have a fixed ratio for all n occurrences, where m=(n-1). In general this property is also valid using lower nL-level points nL-n-pi (i<(n-1)/2) as origin and connecting them with their corresponding lower (n-1)L-level points.
- When n=odd there are two Reflective Orthogonal Axes (nL-o-2L1) at Morley’s 1st Orthocenter X bisecting the n versions of angles mL-n-p((n-1)/2).X.mL-n-p((n/2)-1), where m=(n-1).
Estimated human page views: 297
