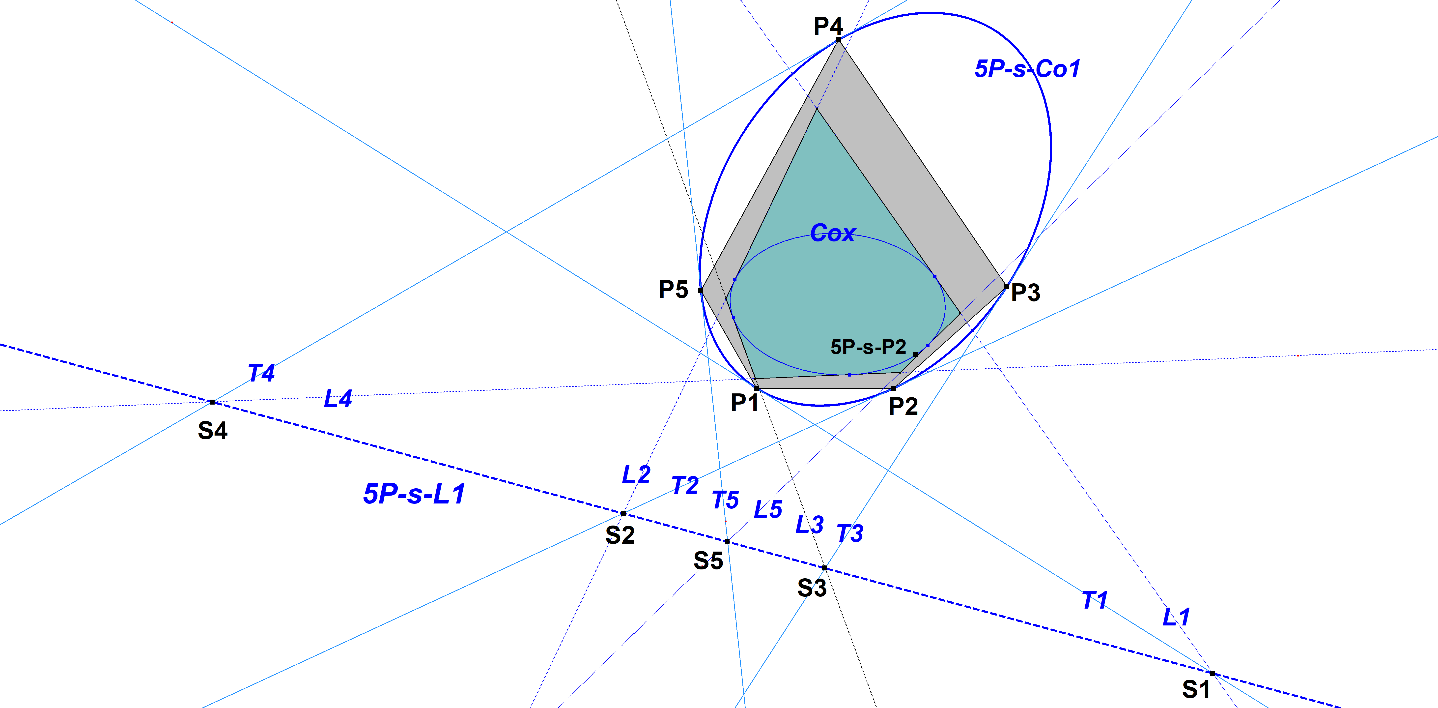
5P-s-L1 5P-Schmidt Line
Given Reference Pentangle 5P(P1,P2,P3,P4,P5).
Let Li be QA-Tf11(Pi) wrt ref-QA (PjPkPlPm). QA-Tf11 is the equivalent of the Trilinear Polar (also called Tripolar) in a Quadrangle (abbreviated QA or 4P).
Let Ti be the tangents of circumscribed conic 5P-s-Co1 with resp. P1,P2,P3,P4,P5.
then points Li ^ Ti are collinear on a new line 5P-s-L1.
Integers i,j,k,l,m each being different numbers from (1,2,3,4,5).
This line was found by Eckart Schmidt. See [66], QPG-messages #359-#362, #365, #367, #368.
The equivalent of 5P-s-L1 in a Pentangle is 5L-s-P11.
Properties
- Let Cox be the Inscribed Conic of (L1,L2,L3,L4,L5). Now point 5P-s-P2 will be lying on Cox (mentioned by Bernard Keizer, see [66], QPG-message #360).
Estimated human page views: 211
