7P-s-P1 7P-Schmidt Point / Singular Focus of Circular Cubic
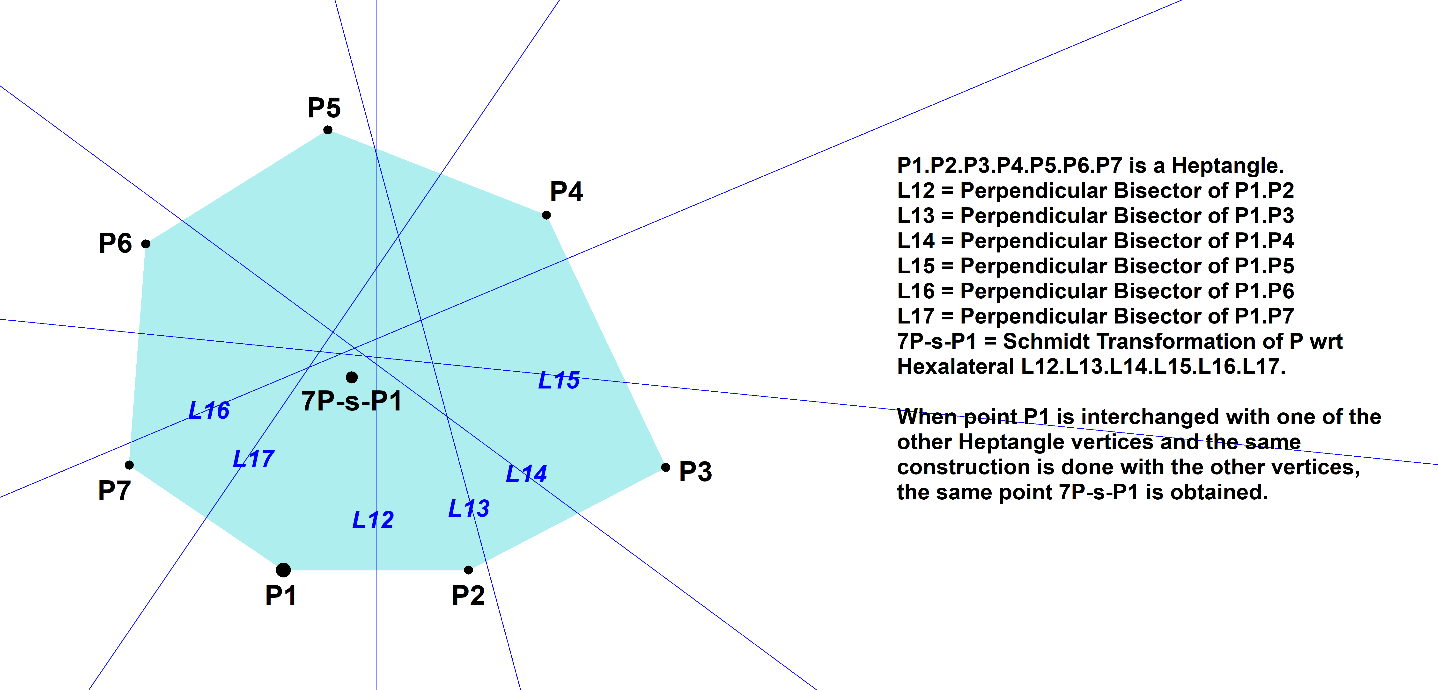
Consider a 7-Point (Heptangle) with vertices Pi (i=1,2,3,4,5,6,7).
Choose one of its vertices Pi.
Construct the perpendicular bisectors Lij of (Pi,Pj), where j unequal i.
In this way Pi defines a 6-Line (Hexalateral) formed by these perpendicular bisectors.
It appears that the 6L-Schmidt Transformation (6L-s-Tf1) wrt to this 6-Line of Pi is independent of the chosen Pi. This fixed point is 7P-s-P1.
This point was found by Eckart Schmidt. See [34], QFG #3552.
Singular Focus of Circular Cubic
7P-s-P1 has another important function. It is the (Singular) Focus of the Circular Cubic (7P-s-Cu1) defined by the 7 vertices of the Reference Heptangle and the circular points at in finity. See [66], QPG-message #665.
A circular cubic has a Focus F, being the point where the tangents at the circular points intersect. See [17c]. This focus is 7P-s-P1. It has also a real asymptote and is cutting its asymptote in a point Q. Any line through Q cuts the circular cubic in 2 points equidistant from the Focus F. See [66], QPG-messages #152-154, #665. #666.
General construction for the singular focus of a circular cubic
Needed for the construction of 7P-s-P1 are the constructions of the submodules QL-Tf1, 5P-s-Tf5, 6P-s-Tf1:
- First we have QL-Tf1 in a 4-Line (reference figure of 4 random Lines) which is a Moebius Transformation swapping the opposite vertices (intersection points of two pairs of reference lines) of a Quadrilateral. We use it for next 5P-point.
- In a 5-Point (reference figure of 5 random Points P1, P2, P3, P4 and P5) 5P-s-P5 is defined as QL-Tf1(P1) wrt the 4-Line formed by the perpendicular bisectors of P1.P2, P1.P3, P1.P4, P1.P5. We use it for next 6P-point.
- There are six 5-Points in a 6-Point (reference figure of 6 random Points) and the six versions of 5P-s-P5 are concyclic on a circle with center 6P-s-P1. We use it for next 7P-point.
- There are seven 6-Points in a 7-Point (reference figure of 7 random Points) and the seven versions of the 6P-s-P1-circle are concurrent in a point 7P-s-P1. This is the singular focus, neatly dependent on 7 points.
Properties
- 7P-s-P1 is:
- fixed point for all 7P’s inscribed in 7P-s-Cu1
- 6P-s-Tf1(X) for 6P inscribed in 7P-s-Cu1 and all X on 7P-s-Cu1
- 6L-s-Tf1(Pi) wrt Perpendicular Bisectors(Pi.Pj), j unequal i
- 6P-s-Ci1 common-circles-intersection of component 6P’s
- QL-P1 for any 7 points on QL-Cu1
- QA-P9 for any 7 points on QA-Cu1
- QA-P41 for any 7 points on QA-Cu7
- See [66], QPG-message 665.
Estimated human page views: 304
