nP-n-Tf1 nP-CC-Moebius Conjugate
The nP-CC-Moebius Conjugate is a Moebius transformation valid for configurations of n points (n = 3, 4, …. ). It maps a point into another point. The transformation is bijective.
It is mentioned at [66], QPG-message #689.
Preamble
The CC-Moebius Conjugate is a Moebius Transformation mapping a point into another point.
When all points on a circle are mapped by a Moebius Transformation the mapped points again form a circle. Therefore it’s said that a Moebius transformation maps circles into other circles. When two circles are transformed the angles under which they meet are preserved.
Lines are also mapped into circles. But lines are supposed to be circles with its center in infinity. Therefore also the notion of “generalized circles” is used, meaning that a circle can degenerate into a line and they are of the same kind.
The Moebius transformation is bijective.
The type of Moebius Transformation used here is represented by the function 1/z in the complex plane. It is the sequence of a circle inversion of a point in a unit circle and the reflection about an axis through the center of that unit circle.
The prefix CC- is used to indicate the role of the CircumCenter in this Conjugate. It all starts with the CircumCenter in a triangle.
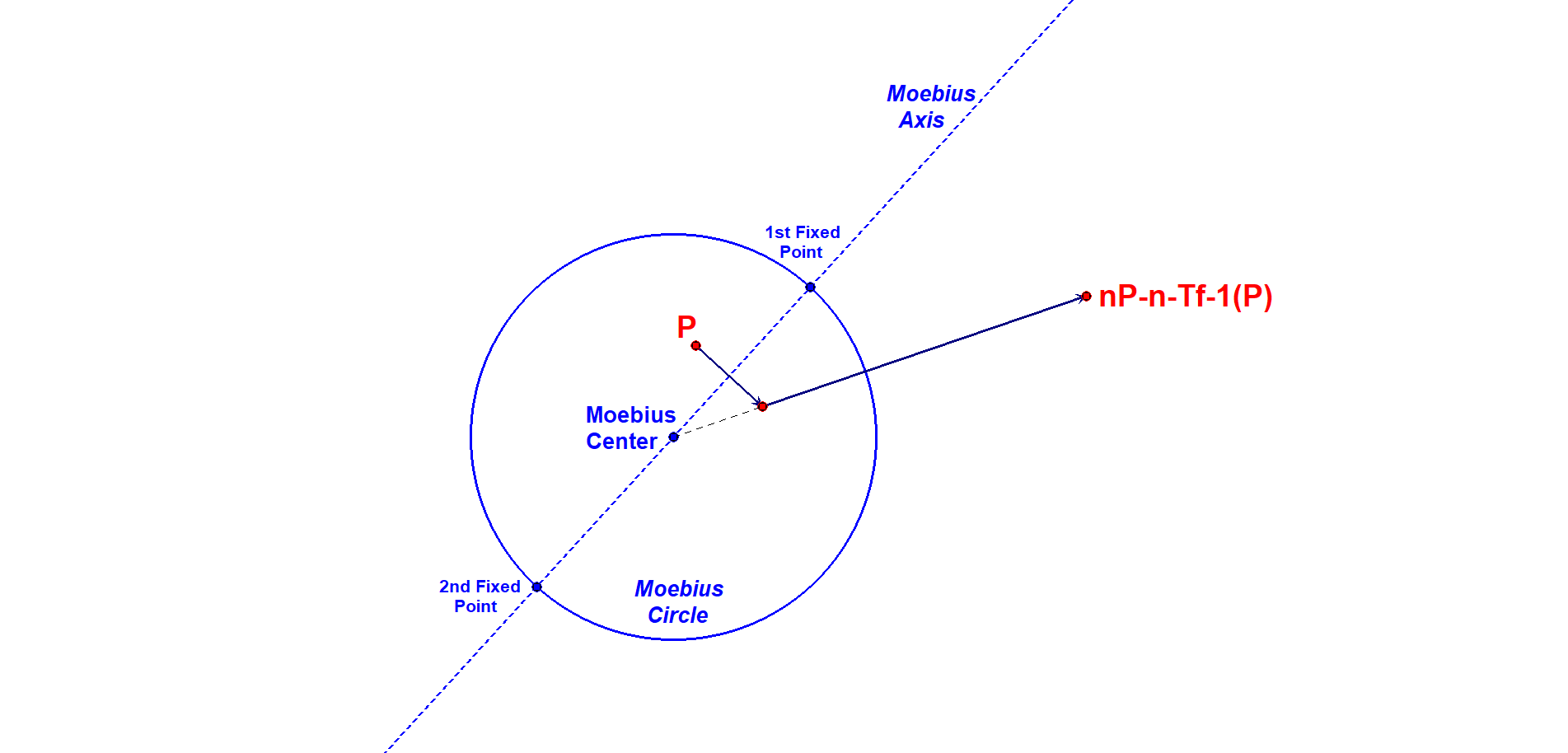
There are 3 basic elements needed for a CC-Moebius Transformation:
- A unit-circle, here called the Moebius Circle.
- The Center of the unit-circle, here called the Moebius Center.
- An axis through the center of the unit-circle, here called the Moebius Axis.
These three elements here will be called the Moebius configuration.
The transformation, mapping P into Q is a sequence of two steps:
- Let R be the reflection of P about the Moebius Axis.
- Let Q be the inverse of R in the Moebius Circle.
Those two steps can be changed in order. The outcome will be the same.
There can be different points Pi being mapped into Qi.
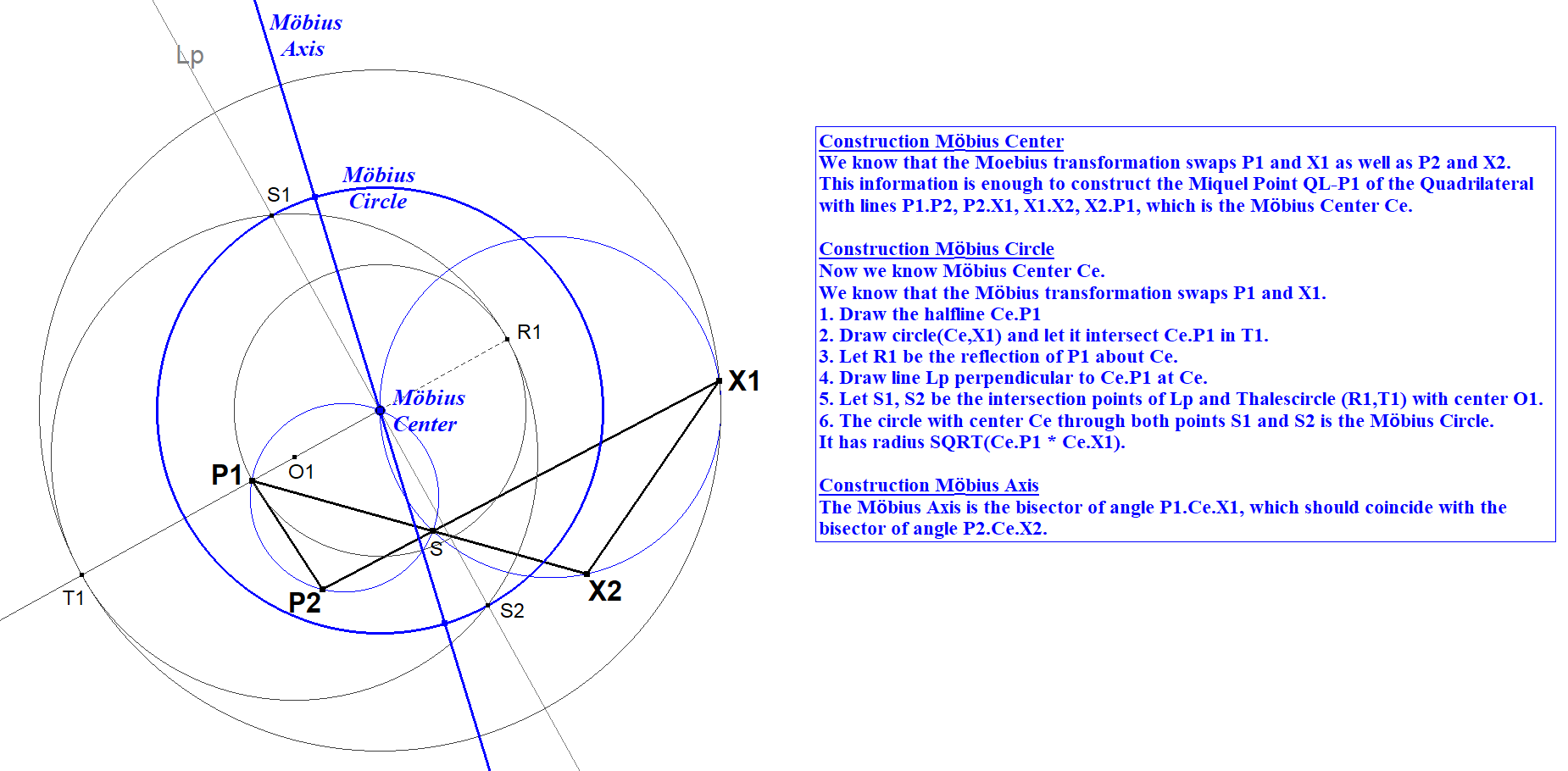
When two pairs (P1,Q1) and (P2,Q2) are known, then the underlying Moebius Circle with Center and Axis can be constructed.
In many instances more than two pairs (Pi,Qi) are known and turn out to have the same Moebius Circle with Center and Axis. This is the case with the nP-CC-Moebius Conjugate, where always per n-Point n pairs (Pi,Qi) will come forward having the same underlying Moebius Configuration.
The method to construct the Moebius constellation will be called here the Pi-Qi-standard Moebius construction. It is described in next picture.
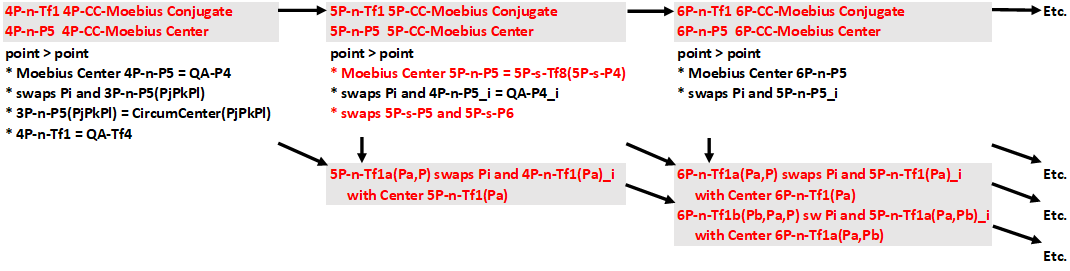
The nP-n-Tf1 Conjugate
After these introductory words we come to the nP-n-Tf1 Conjugate.
Per n-Point there will be an nP-CC Moebius Configuration with Moebius Center nP-n-P5 and an nP-CC Moebius Conjugate nP-n-Tf1. As soon as this information is known the (n+1)P-CC Moebius Configuration can be constructed using the nP-n-P5 Moebius Center of the n-level before.
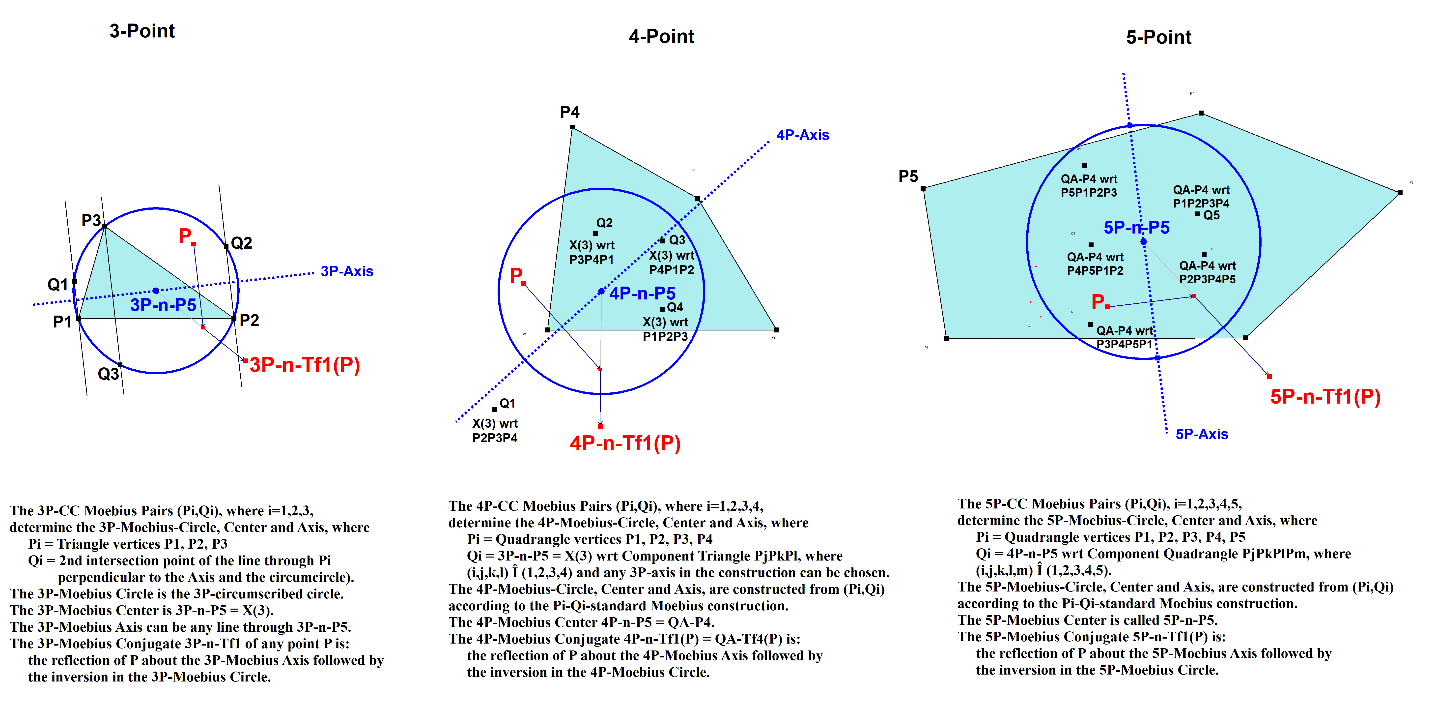
- It starts with a 3-Point / Triangle. There the 3P-CC Moebius Configuration is defined by a Moebius Configuration with the 3P-circumcircle as the Moebius Circle and some line through the circumcenter (any line) as the Moebius Axis. Therefore the 3P-Moebius Center 3P-n-P5 will be X(3) and the conjugate 3P-n-Tf1 can be constructed because Moebius Circle, Center and Axis are known.
- Then in a 4-Point / Quadrangle with vertices P1, P2, P3, P4 we have 4 Component Triangles each with its own 3P-Moebius Center Q1 = 3P-n-P5_1, Q2 = 3P-n-P5_2, Q3 = 3P-n-P5_3, Q4 = 3P-n-P5_4. This leads to 4 pairs (P1,Q1), (P2,Q2), P3,Q4), (P4,Q4) which generate a 4P-Moebius Configuration with a 4P-Moebius Center 4P-n-P5 and a 4P-Moebius Conjugate 4P-n-Tf1.
- Then in a 5-Point / Pentangle with vertices P1, P2, P3, P4, P5 we have 5 Component Triangles each with its own 4P-Moebius Center Q1 = 4P-n-P5_1, Q2 = 4P-n-P5_2, Q3 = 4P-n-P5_3, Q4 = 4P-n-P5_4, Q4 = 4P-n-P5_5. This leads to 4 pairs (P1,Q1), (P2,Q2), P3,Q4), (P4,Q4) which generate a 5P-Moebius Configuration with a 5P-Moebius Center 5P-n-P5 and a 5P-Moebius Conjugate 5P-n-Tf1.
- And so forth for a 6-Point, 7-Point, 8-Point, etc..
See next picture for the first three n-levels.
5P-n-Tf1 is already mentioned as “csc3” in [34], QFG-messages #3660, #3679.
Properties
Extension to the nP-n-Tf1 Moebius Conjugate
There are these related Moebius Conjugates:
- nP-n-Tf1a swaps Pi and (n-1)P-n-Tf1(Pa)
with Center nP-n-Tf1(Pa), Pa being an added random point
- nP-n-Tf1b swaps Pi and (n-1)P-n-Tf1a(Pb)
- with Center nP-n-Tf1a(Pa,Pb), Pa,Pb being added random points
- nP-n-Tf1c swaps Pi and (n-1)P-n-Tf1b(Pc)
- with Center nP-n-Tf1b(Pa,Pb,Pc), Pa,Pb,Pc being added random points
- etc. ad infinitum
NOTE: the conjugate nP-n-Tf1x(Pi, .. , Pn), Pi,..,Pn can be taken in any order (gives the same result)
The advantage of these extended conjugates is that for every n-Point any point P can be referred to as a Moebius Center of a Moebius Transformation, being nP-n-Tf1a with Pa=nP-n-Tf1(P).
Properties
- 5P-n-Tf1a(5P-s-P5, P) = 5P-s-Tf8(P)
- 5P-n-Tf1a(5P-s-P5, 5P-n-P5) = 5P-s-P4
- Moebius Center 5P-n-Tf1a(5P-s-P5, P) = 5P-s-P6
- Moebius Center 5P-n-Tf1a(5P-s-P6, P) = 5P-s-P5
Estimated human page views: 140
