QA-4Tr1: QA-Component Triangles
A Quadrangle has 4 defining random points P1, P2, P3, P4 without preference or order.
With these points 4 sets of 3 different points can be formed:
- P1, P2, P3
- P1, P2, P4
- P1, P3, P4
- P2, P3, P4
Ordened Component Triangles
These 4 sets define 4 triangles also called the Component Triangles of a Quadrangle.
In certain cases the order within these triangles are of importance.
Well known is that in a Quadrangle all Component Triangles are perspective with the QA-Diagonal Triangle. However the vertices of the Component Triangles are specific and ordened wrt the QA-Diagonal Triangle.
First of all we have to define the vertices of the QA-Diagonal Triangle in an ordened way.
The vertices of the QA-Diagonal Triangle can be seen as the Diagonal Crosspoints of the 3 Component Quadrigons (See QA-3QG1).
These 3 Component Quadrigons are:
- P1.P3.P2.P4 with Diagonal Crosspoint S2.
- P1.P2.P3.P4 with Diagonal Crosspoint S3.
- P1.P2.P4.P3 with Diagonal Crosspoint S4.
Note that the serial number of the Diagonal Crosspoint corresponds to the serial number of the point opposite to P1 in the Quadrigon.
Now S2.S3.S4 is the QA-Diagonal Triangle QA-Tr1.
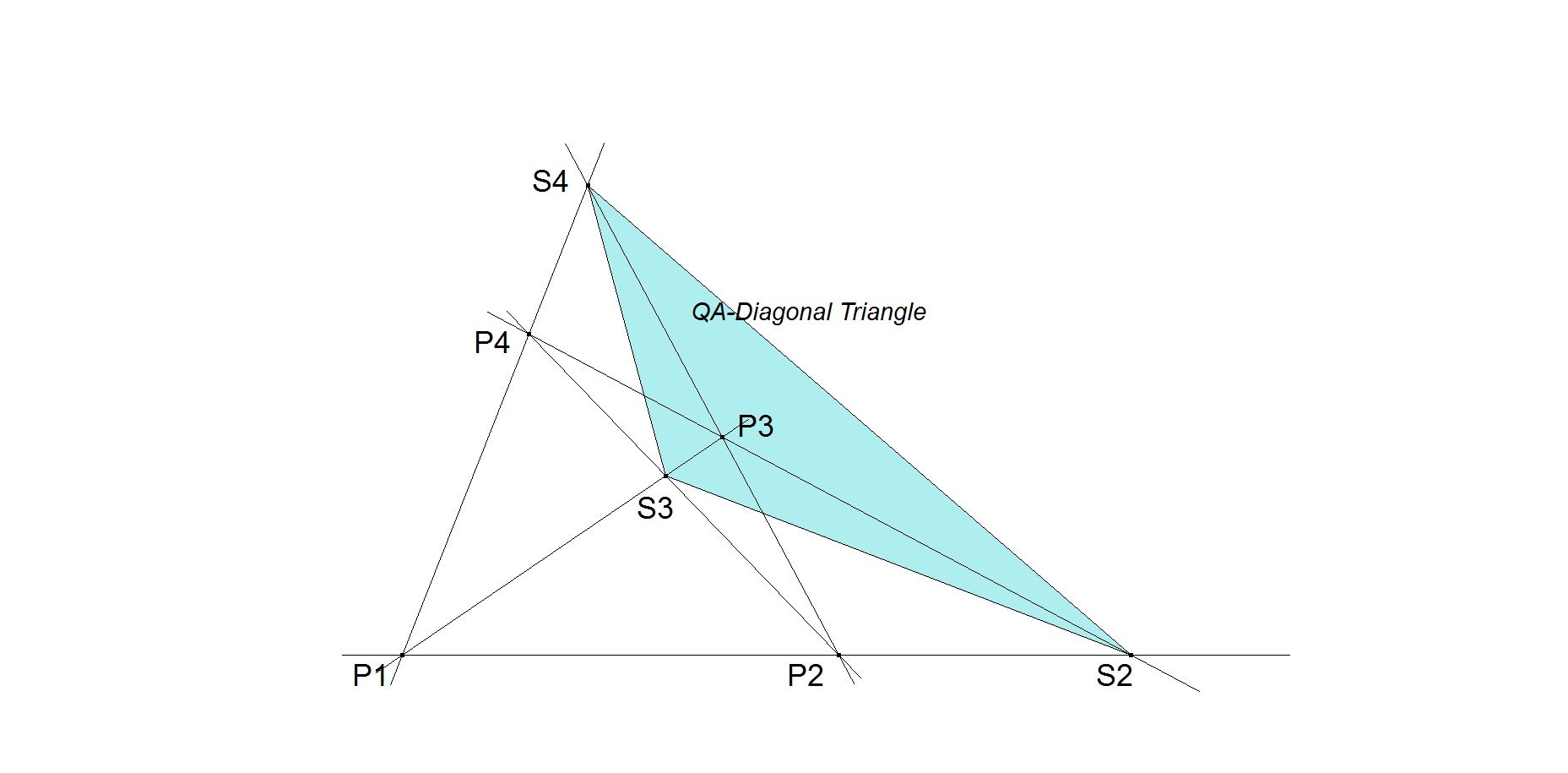
Defining the vertices of the QA-Diagonal Triangle this way we can see in a picture that S2.S3.S4 is perspective with P2.P3.P4.
The other Component Triangles to be perspective with the QA-Diagonal Triangle are P1.P4.P3, P4.P1.P2, P3.P2.P1.
Now the Component Triangles with vertices in the right order to be perspective with QA-Diagonal Triangle:
- P2 . P3 . P4,
- P1 . P4 . P3,
- P4 . P1 . P2,
- P3 . P2 . P1.
Relationship with QA-Triple Triangles
The order of vertices of the QA-Component Triangles also will be of importance when comparing with other triangles built also from QA-Quadrigons. These triangles are also called QA-Triple Triangles (see QA-Tr-1).
The types of relations between a QA-Triple Triangle and simultaneously the 4 QA-Component Triangles are called:
- Quadri-Perspective relation (examples see QA-Tr-2)
- Quadri-Orthologic relation (examples see QA-Tr-3)
- Quadri-Cyclologic relation (examples see QA-Tr-4).
Estimated human page views: 665
