QA-2Co1: Pair of Circumscribed QA-Parabolas
Two parabolas can be constructed from 4 points.
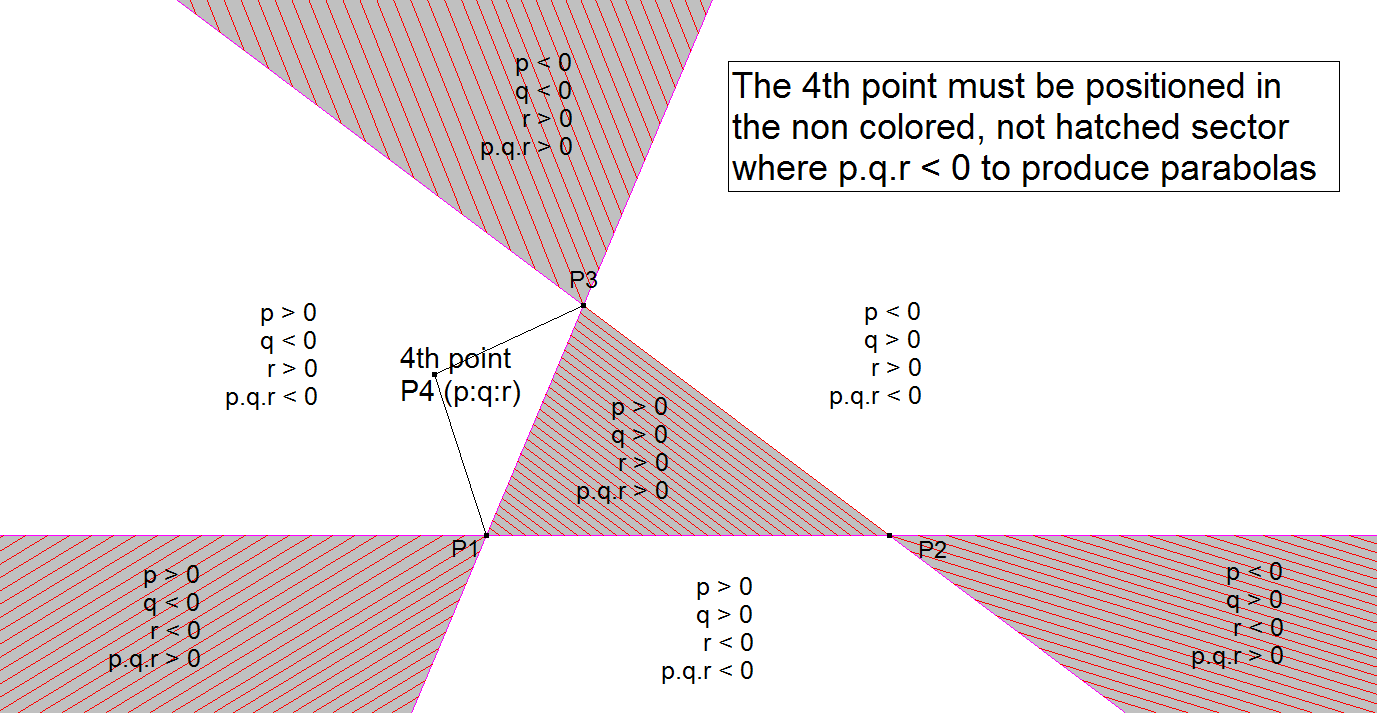
There are however some limitations to the positioning of these points for having a real solution of these parabolas.
- No 3 of the 4 points must be collinear.
- A Quadrangle consists of 3 Quadrigons.
- These 3 component quadrigons of a Quadrangle are either
- * concave/concave/concave, or
- * convex/crossed/crossed.
- The first situation does not produce a real solution for circumscribed parabolas. So the best way to describe the positioning of 4 points producing circumscribed parabolas is by stating that these 4 points must not bound a concave form.
- This can be confirmed from the formulas.
- It contains the element √(-p q r (p+q+r)). Now (p+q+r) is always > 0 because barycentric coordinates represent areas and the sum of the 3 areas = area of the reference triangle. So √(-p q r (p+q+r)) is only real when p.q.r is negative. That is only when the 4th point in a Quadrigon is a potential mirror point across the sides of the triangle and not across the vertices or inside the triangle as shown in next picture.
The construction of the 2 circumscribed parabolas was described by Newton. This method can be found at [7] as well as [14]. Calculation of the infinity points according to this method delivers these coordinates:
Parabola Equations CT-notation:
r (pq-pr+qr+q2) x y – q (pq-pr-qr-r2) x z – p (q+r)2 y z + 2 Tc (r x y – q x z) = 0
Infinity points CT-notation:
( p (q + r) : –p q – Tc : –p r + Tc )
( p (q + r) : –p q + Tc : –p r – Tc )
where Tc = √(-p q r (p+q+r))
Parabola Equations DT-notation:
(p2-q2+r2) (q2 x2-p2 y2)+(p2+q2-r2) (r2 x2-p2 z2) + Td ((q2-r2) x2-p2 (y2-z2)) = 0
Infinity points DT-notation:
(2 p2 : -p2-q2+r2 – Td : -p2+q2-r2 + Td)
(2 p2 : -p2-q2+r2 + Td : -p2+q2-r2 – Td)
where Td = √ ((p-q-r) (p+q-r) (p-q+r) (p+q+r))
The Parabola infinity points are equal to the infinity points of the Nine-point Conic.
Properties
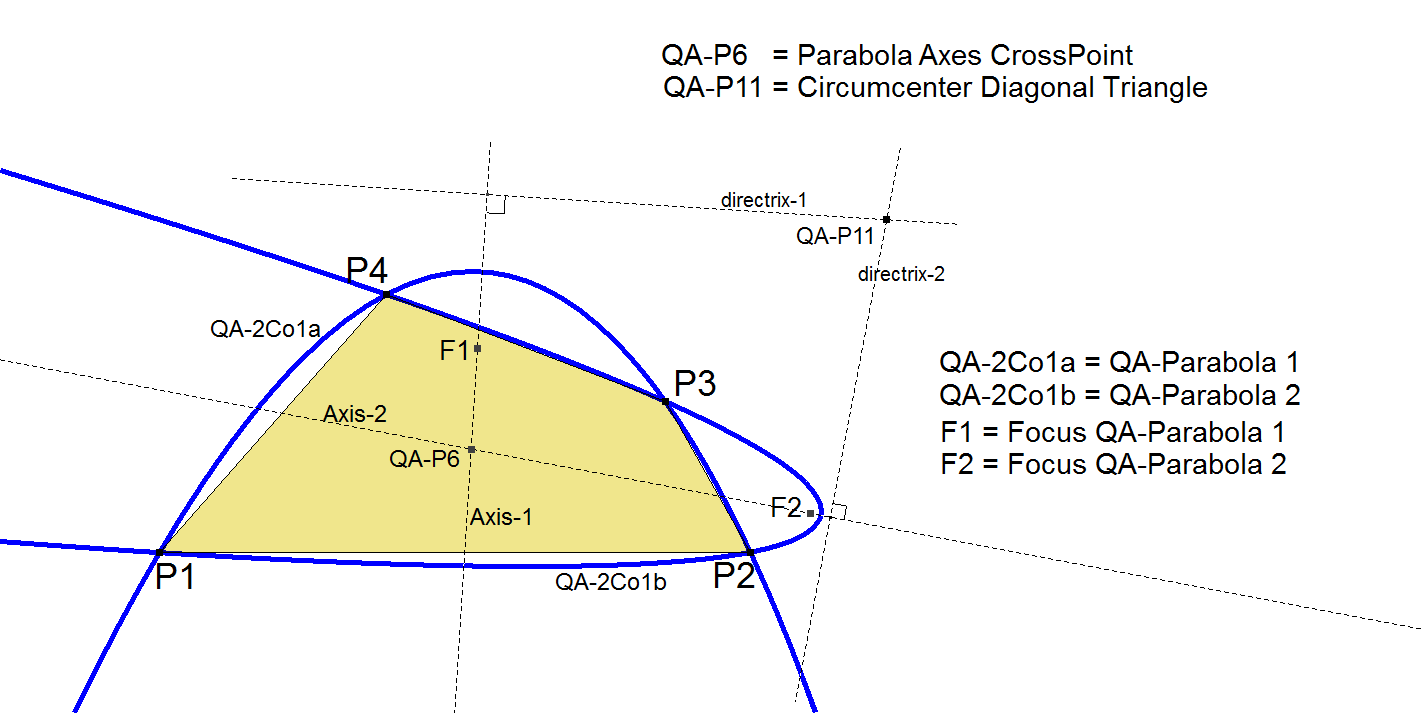
- The sides of the Medial Triangle (of the QA-Diagonal Triangle) are tangential to both circumscribed Quadrangle Parabolas.
- The foci of both circumscribed Quadrangle Parabolas lie on the circumcircle of the Medial Triangle (MT) of the QA-Diagonal Triangle (= Nine-point Circle of the QA-Diagonal Triangle).
- The foci of both circumscribed Quadrangle Parabolas are concyclic with QA-P11 and the involutary conjugate of QA-P11.
- The directrices of both parabolas intersect in QA-P11 (the Circumcenter of the QA-Diagonal Triangle).
- The axes of both parabolas intersect in QA-P6 (the Parabola Axes Crosspoint) which is the Midpoint of QA-P2 (Euler-Poncelet Point) and QA-P4 (Isogonal Center).
- The axes of both parabolas are parallel to the asymptotes of the Nine-point Conic.
- The QA-Diagonal Triangle (QA-Tr1) is self-polar wrt QA-2Co1a and QA-2Co1b.
Estimated human page views: 627
