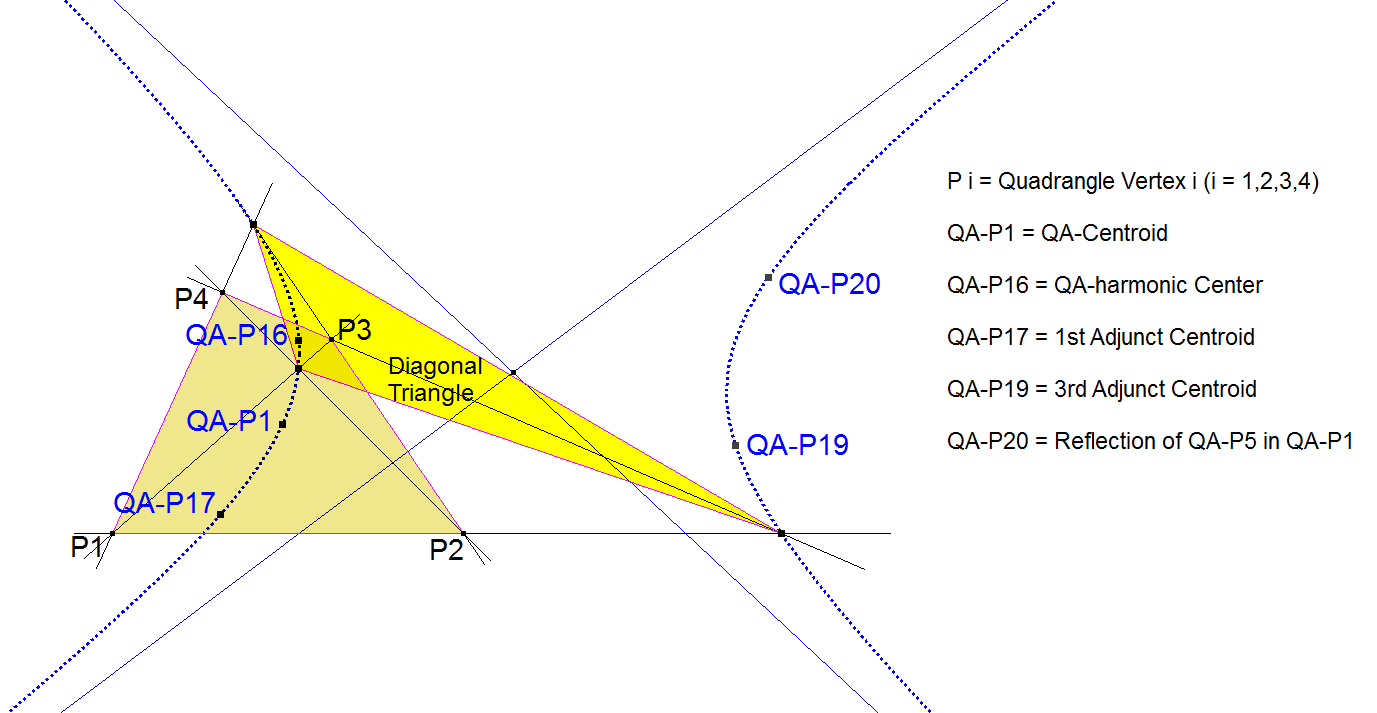
QA-Co5: QA-DT-P1-P16 Conic
QA-Co5 is the circumscribed conic of the Diagonal Triangle of the Reference Quadrangle passing through the QA-Centroid (QA-P1) and the QA-Harmonic Center (QA-P16).
Conic-equation in CT-notation:
p q r (r – q) (p + 2 q + r) (p + q + 2 r) x2
+ p q r (p – r) (p + q + 2 r) (2 p + q + r) y2
+ p q r (q – p) (2 p + q + r) (p + 2 q + r) z2
+ r (q2 – p2) (p + q + 2 r) (-p q + p r + q r + r2) x y
+ q (p2 – r2) (p + 2 q + r) ( p q + q2 – p r + q r) x z
+ p (r2 – q2) (2 p + q + r) ( p2 + p q + p r – q r) y z = 0
Conic-equation in DT-notation:
(p2-q2) r2 (p2+q2-r2) x y+q2 (-p2+r2) (p2-q2+r2) x z+p2 (q2-r2) (-p2+q2+r2) y z = 0
——————————————————————————————————————————————–
1st coordinate Conic Center CT-notation:
p (q + r) (2 p + q + r)
(3 p4 q2 + 6 p3 q3 + 3 p2 q4 – 4 p4 q r – 2 p3 q2 r – 6 p2 q3 r – 8 p q4 r + 3 p4 r2 – 2 p3 q r2 + 2 p2 q2 r2 – 4 p q3 r2 + 5 q4 r2 + 6 p3 r3 – 6 p2 q r3 – 4 p q2 r3 + 8 q3 r3 + 3 p2 r4 – 8 p q r4 + 5 q2 r4)
1st coordinate Conic Center DT-notation:
(p2 – q2 – r2) (q2 – r2)2
——————————————————————————————————————————————–
1st CT-Coordinate QA-DT-Conic-Perspector (see QA-Co-1):
q r (2 p + q + r) (2 p4 + 4 p3 q + p2 q2 – p q3 + 4 p3 r + 4 p2 q r – p q2 r + q3 r + p2 r2 – p q r2 + 2 q2 r2 – p r3 + q r3)
1st DT-Coordinate QA-DT-Conic-Perspector (see QA-Co-1):
p2 (p2 – q2 – r2) (p4 q2 – 2 p2 q4 + q6 + p4 r2 + 4 p2 q2 r2 – q4 r2 – 2 p2 r4 – q2 r4 + r6)
Properties
- QA-Co5 passes apart from the vertices of the Diagonal Triangle also through:
- QA-P1 (QA-Centroid),
- QA-P16 (QA-Harmonic Center),
- QA-P17 (Involutary Conjugate of QA-P5),
- QA-P19 (AntiComplement of QA-P16 wrt the QA-Diagonal Triangle),
- QA-P20 (Reflection of QA-P5 in QA-P1),
- as well as the intersection point QA-P5.QA-P16 ^ QA-P10.QA-P17,
- as well as the Involutary Conjugates of QA-P22, QA-P25, QA-P26.
- QA-Co5 is the Involutary Conjugate of QA-L3 (QA-Centroids Line).
- The tangents to QA-Co5 at QA-P16 and QA-P17 intersect at QA-P18 (Randy Hutson, July, 2012).
- The QA-DT-Conic-Perspector (see QA-Co-1) is a point on the line QA-P16.QA-P17 (Randy Hutson, July, 2012).
Estimated human page views: 595
