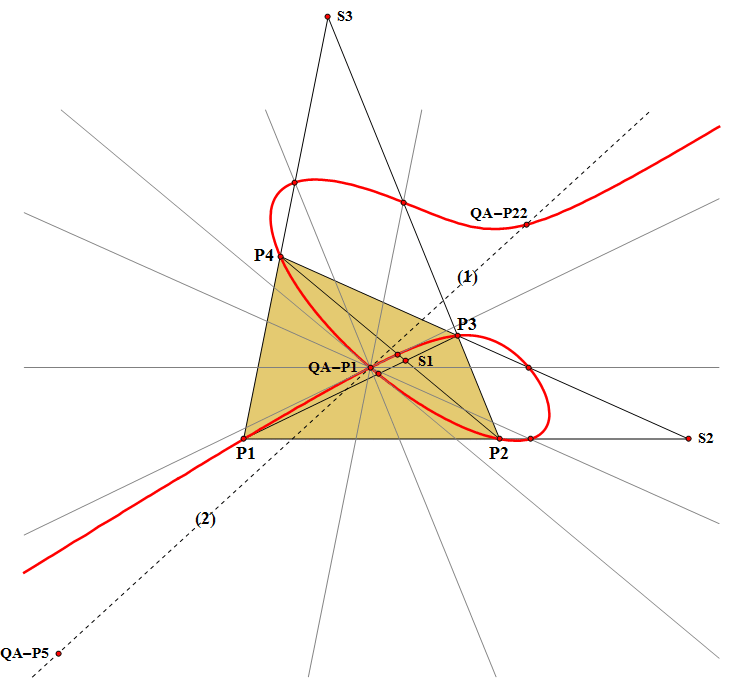
QA-Cu6: QA-P1-Involution Center Cubic
This cubic is the locus of the involution centers of all lines passing through QA-P1 (Quadrangle-Centroid). So it is the locus of Midpoints of the Involutary Conjugates on the cubic QA-Cu5.
The involution is created by the intersection points of the QA-P1-line with the sides of Quadrigon P1.P2.P3.P4 (see chapter QA-Tf1: QA-Line Involution)
QA-P22, the Reflection of the Midpoint (QA-P1,QA-P5) in QA-P1 also lies on the cubic.
Similar cubics can be constructed by taking involution centers of lines passing through another point than QA-P1. The other 2 QA-quadrigons deliver the same cubic. This makes the cubic a real QA-Cubic.
Equation CT-notation:
r (p+q+2r) ((3q+p)x–(3p+q) y) x y
+ q (p+2q+r) ((3p+r) z–(3r+p) x) z x
+ p (2p+q+r) ((3r+q) y–(3q+r) z) y z – (p-q)(q-r)(r-p) x y z = 0
Equation DT-notation:
q2 r2 (q2 – r2) x3 + q2 r2 (2 p2 (y – z) – (q2 – r2) (y + z)) x2
+ p2 r2 (r2 – p2) y3 + p2 r2 (2 q2 (z – x) – (r2 – p2) (x + z)) y2
+ p2 q2 (p2 – q2) z3 + p2 q2 (2 r2 (x – y) – (p2 – q2) (x + y)) z2 = 0
Properties
- The vertices of the Quadrangle and the Midpoints of the Diagonal triangle and QA-P1, QA-P22 lie on this cubic.
- The intersection point QA-P1.QA-P6 ^ QA-P22.QA-P29 lies on this cubic.
- The intersection points of the lines through QA-P1 parallel to the QA-sidelines with the opposite sidelines all lie on this cubic.
Estimated human page views: 654
