QA-6: QA-Conversion CT -> DT – coordinates
Let P1.P2.P3.P4 be the Reference Quadrangle.
Let P1.P2.P3 be the random Reference Component Triangle en let P4 be the 4th point.
The QA-Diagonal Triangle S1.S2.S3 is the Cevian Triangle of P4 wrt P1.P2.P3.
Let Q be some point to be converted from CT- to DT-coordinates.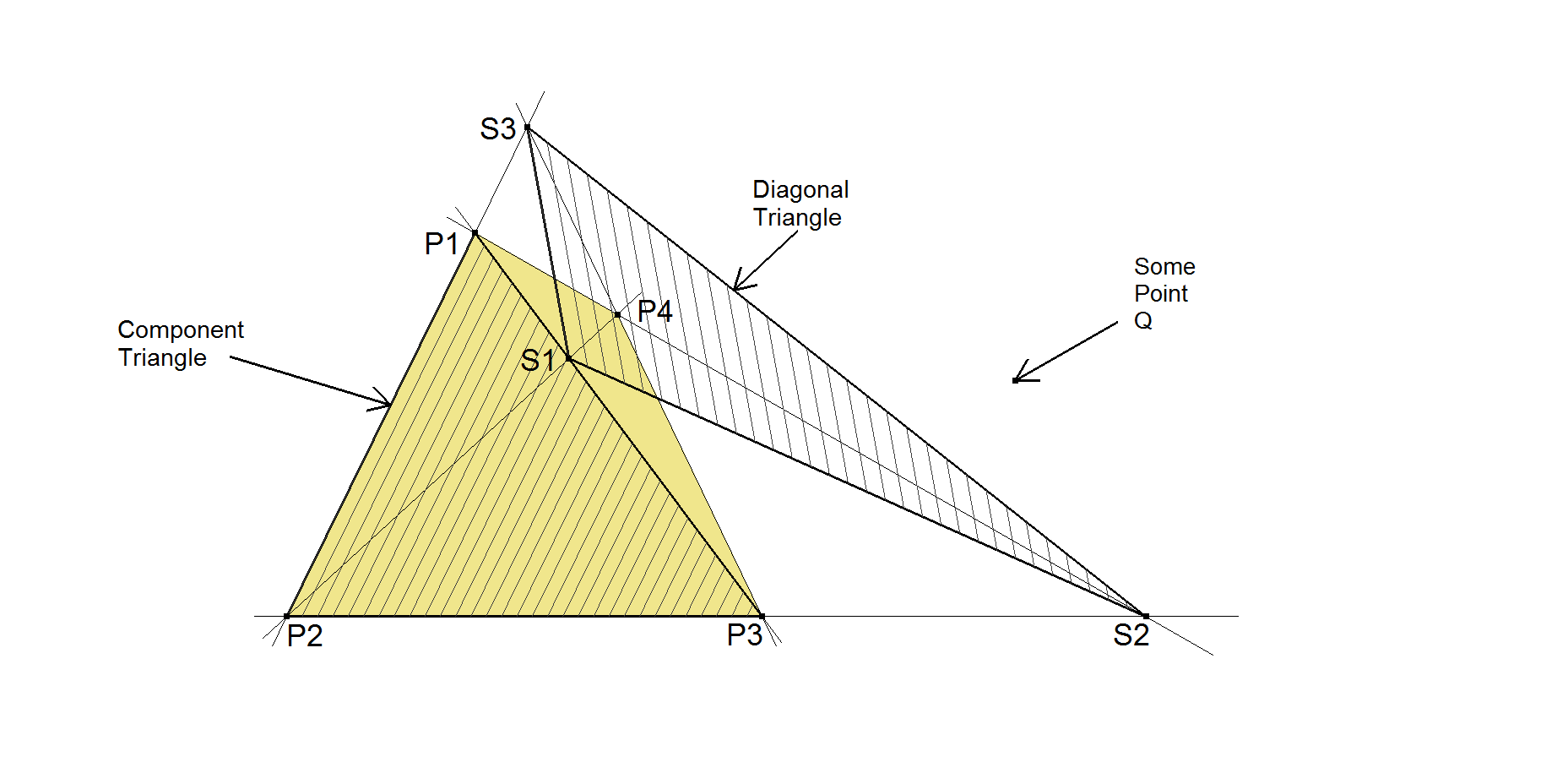
Let Qc (xc : yc : zc) be the presentation of Q in barycentric coordinates wrt the Reference Component Triangle.
Let Qd (xd : yd : zd) be the presentation of Q in barycentric coordinates wrt the Diagonal Triangle.
Now Qc = xc.cfc1.P1 + yc.cfc2.P2 + zc.cfc3.P3 wrt the Reference Component Triangle and
also Qd = xd.cfd1.S1 + yd.cfd2.S2 + zd.cfd3.S3 wrt the Diagonal Triangle,
where:
- (xc : yc : zc) are the barycentric coordinates of Q wrt the Component Triangle,
- (xd : yd : zd) are the barycentric coordinates of Q wrt the Diagonal Triangle,
- cfc1, cfc2, cfc3 are the Compliance Factors of the Component Triangle,
- cfd1, cfd2, cfd3 are the Compliance Factors of the Diagonal Triangle.
Explanation of Compliance Factors can be found at (Ref-26).
Since the Component Triangle is the Reference Triangle, the Compliance Factors of the Component Triangle are all equal 1.
The Compliance Factors of the Diagonal Triangle are:
- cfd1 = Det [Gd, S2, S3] / Det [S1, S2, S3],
- cfd2 = Det [S1, Gd, S3] / Det [S1, S2, S3],
- cfd3 = Det [S1, S2, Gd] / Det [S1, S2, S3],
where Gd = the Centroid of the Diagonal Triangle and “Det” is the abbreviation for “Determinant”.
Calculation gives 2 presentations of the coordinates of Q wrt the Component Triangle:
- Qc = (xc : yc : zc),
- Qd = (p (q+r) (p yd + q yd + p zd + r zd) : q (p+r) (p xd + q xd + q zd + r zd) : r (p+q)(p xd + r xd + q yd + r yd))
Since Qc and Qd present the same point we can now calculate the coordinates of Q wrt the Diagonal Triangle:
- (xd : yd : zd) = ((q+r)(q r xc - p r yc - p q zc) : (p+r)(-q r xc + p r yc - p q zc) : (p + q)(-q r xc - p r yc + p q zc)).
However we have to bear in mind that the variables in these coordinates are expressions in (a,b,c) and (p,q,r), which are variables wrt the Component Triangle.
Therefore the CT > DT-conversion of P(x : y : z) consists of these 3 consecutive steps:
1. Transform: (x : y : z) --> ((q + r) (q r x - p r y - p q z) : (p + r) (-q r x + p r y - p q z) : (p + q) (-q r x - p r y + p q z))
2. Replace: a2 --> (4 p2 (SA q2 + SB q2 - 2 SA q r + SA r2 + SC r2)) / ((p + q - r)2 (p - q + r)2)
b2 --> (4 q2 (SA p2 + SB p2 - 2 SB p r + SB r2 + SC r2)) / ((p - q - r)2 (p + q - r)2)
c2 --> (4 r2 (SA p2 + SC p2 - 2 SC p q + SB q2 + SC q2)) / ((p - q - r)2 (p - q + r)2) .
3. Replace: p --> (-p + q + r)
q --> (+p - q + r)
r --> (+p + q - r)