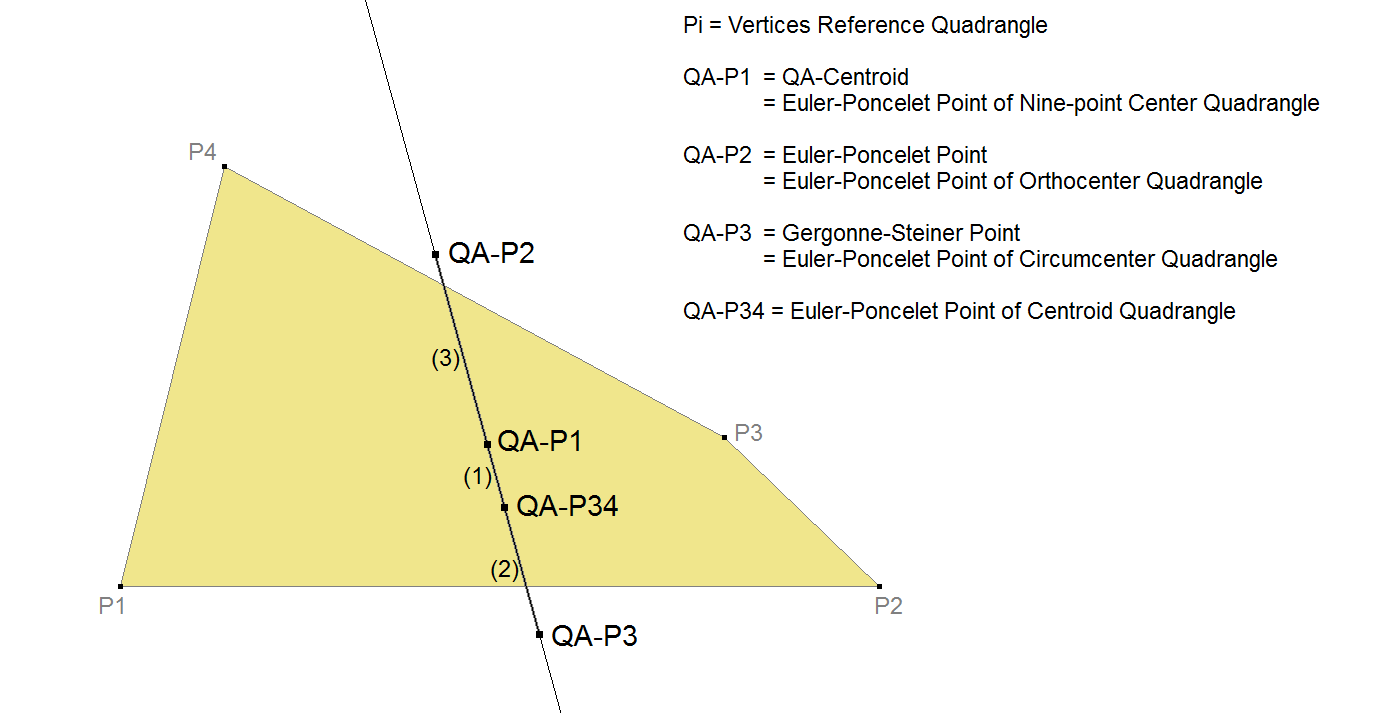
QA-L1: QA-P1-P2-P3 Line

QA-L1: QA-P1-P2-P3 Line

The QA-L1-line is the line through QA-P2 (Euler-Poncelet Point) and QA-P3 (Gergonne-Steiner Point). Both points are constructed in a similar way. They are both common points of circles through midpoints of line segments between Quadrangle points.

QA-P1 (Centroid) also lies on this line and is Midpoint (QA-P2,QA-P3).

Of next 4 points on QA-L1 it also appears that:

QA-P1 is the Euler-Poncelet Point of the Nine-point Center Quadrangle.
QA-P2 is the Euler-Poncelet Point of the Orthocenter Quadrangle.
QA-P3 is the Euler-Poncelet Point of the Circumcenter Quadrangle.
QA-P34 is the Euler-Poncelet Point of the Centroid Quadrangle.

QA-P1, QA-P2, QA-P3 and QA-P34 have mutual distance ratios similar to their corresponding points in the Triangle Environment on the Euler Line.

Coefficients:

1st CT-coefficient:

a⁴ q (q - r)r/(q+r) + b⁴ p r (p+2q+r)/(p+r) – c⁴ p q(p+q+2r)/(p+q)

– b² c²p (q-r) + a²c²q (p+3r) – a² b² r (p+3q)

1st DT-coefficient:

p² (b² r² - c² q²) (b² r² (p²+ q²- r²) + c² q² (p²- q² + r²) - 2 a² q² r²)

Properties:

QA-L1 = QA-P1.QA-P2 // QA-P22.QA-P29
QA-L1 is the QA-L2 line of the Nine-point Center Quadrangle (Eckart Schmidt, August 24, 2012).
The Orthopole (see Ref-13) of QA-P3.Pi wrt triangle Pj.Pk.Pl, for all (i,j,k,l) ∈ (1,2,3,4) lie on the circle with diameter QA-L1-line segment QA-P2.QA-P3. See Ref-11, Hyacinthos messages 21865 & 21867.

MATHEMATICS

Plaats reactie