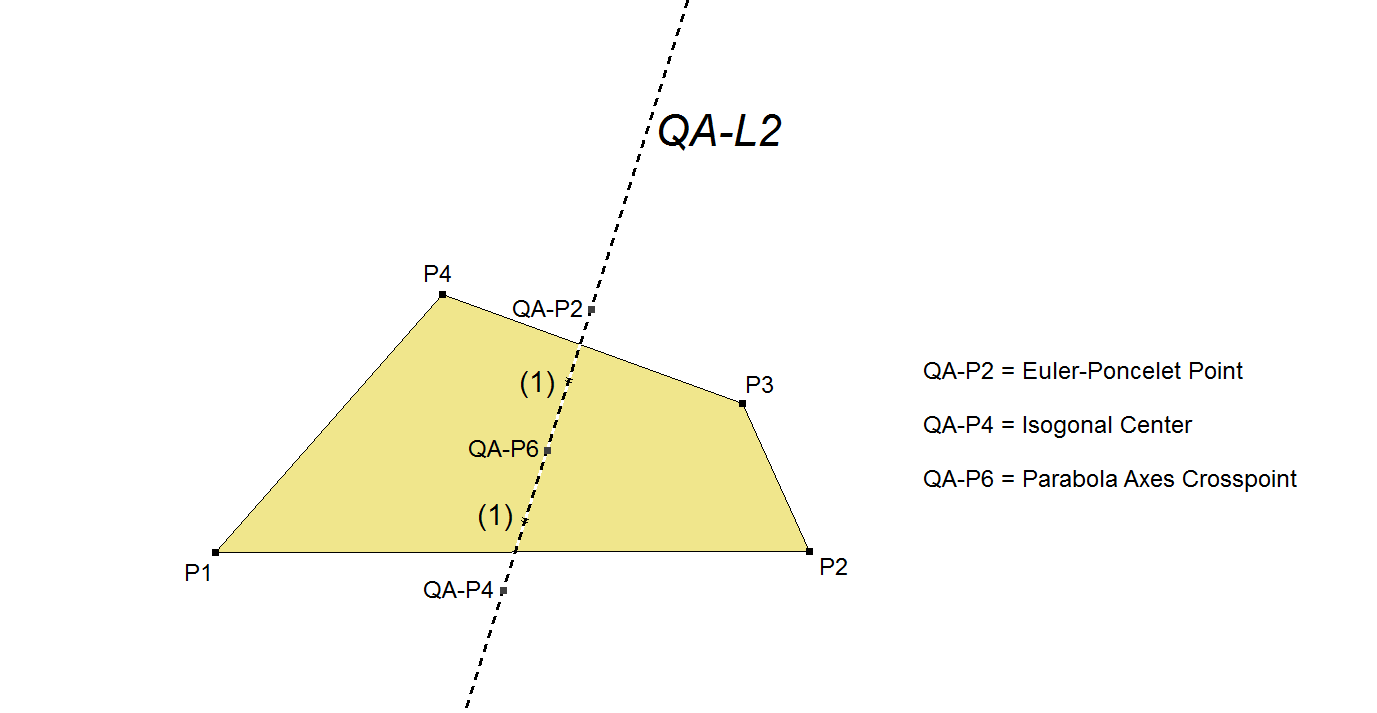
The QA-L2-line is the line through QA-P2 (Euler-Poncelet Point) and QA-P4 (Isogonal Center). QA-P6 (Parabola Axes Crosspoint) also lies on this line and is their Midpoint. The expression of the line is not a simple one.
Coefficients:
1st CT-coefficient:
b2 p r2 (SA p - SB q) ((b2 - a2) p q + b2 p r - a2 q r) (b2 p r + (b2 - a2) p q + (b2 - c2) q r - 2 SB q2)
- c2 p q2 (SA p - SC r) ((c2 - a2) p r + c2 p q - a2 q r) (c2 p q + (c2 - a2) p r + (c2 - b2) q r - 2 SC r2)
1st DT-coefficient:
(c2 q2-b2 r2)
(-a2 p2 (c4 q4+b4 r4) + (b4 p4+a4 q4) r2 SB + q2 (c4 p4+a4 r4) SC + 2 a2 p2 q2 r2 (SA2-SB SC))
(-a2 p2 (c4 q4+b4 r4) + (b4 p4+a4 q4) r2 SB + q2 (c4 p4+a4 r4) SC + 2 a2 p2 q2 r2 (SA2-SB SC))
Properties:
- QA-L2 = QA-P2.QA-P4 // QA-P1.QA-P32 // QA-P7.QA-P8 // QA-P12.QA-P24 // QA-P11.QA-P38
- QA-L2 and the 5th Point Tangent at QA-P2 are orthogonal. See QA-Tf9 and QA-4.
- QA-L2 and the asymptote of QA-Cu7 (QA-Quasi Isogonal Cubic) are perpendicular. See QA-Cu7 and QA-4.