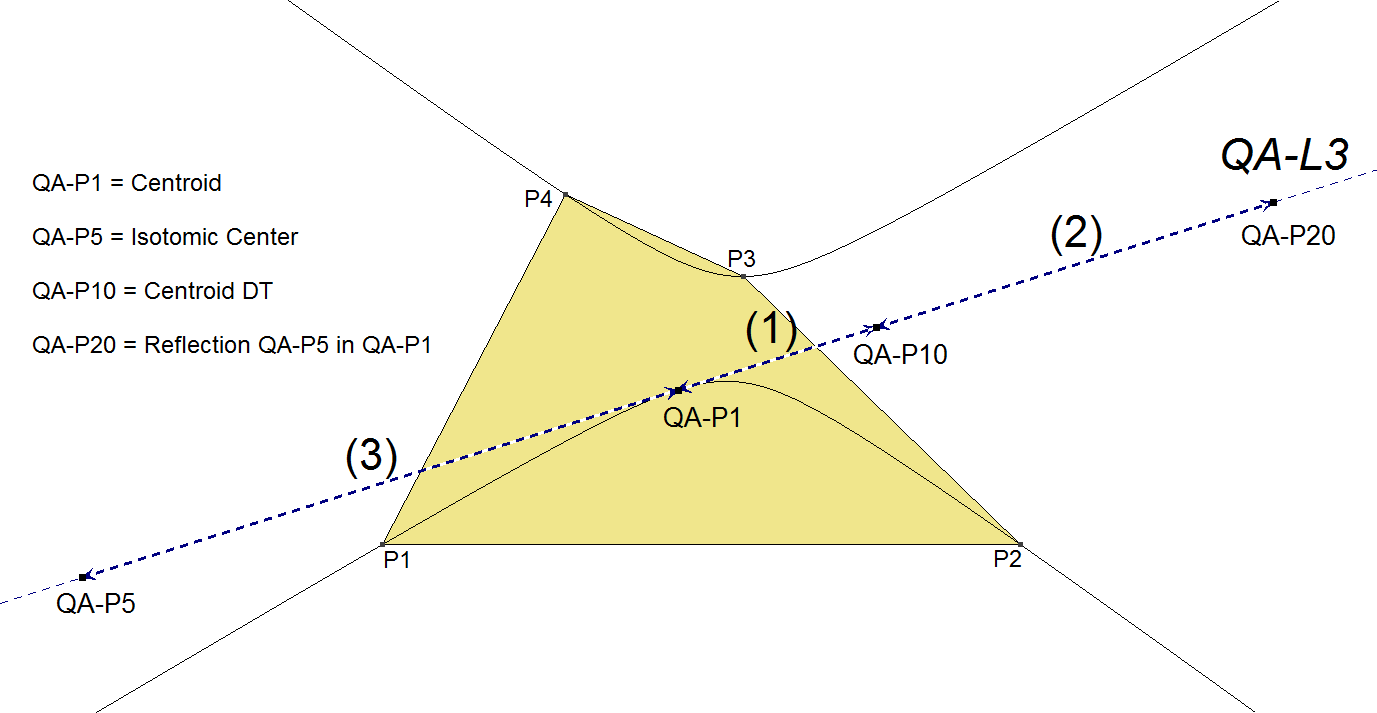
QA-L3: QA-P1-P5-P10 Line or Centroids-Line
The QA-L3-Line is the line through the Centroid of the Quadrangle (QA-P1) and the Centroid of the Diagonal Triangle of the Quadrangle (QA-P10). It also passes through the Isotomic Center (QA-P5) and the 1st and 2nd QA-Quasi Centroids (QA-P25 and QA-P26).
Interestingly, all these points have coordinates independent of (a,b,c). As a consequence the coefficients of QA-L3 also are independent of (a,b,c).
Because the Centroid of the Quadrangle is on this line and it is divided in segments of fixed ratio this line has the allure of the Euler Line in Triangle environment.
1st CT-coefficient:
p (q – r) / (2p + q + r)
1st DT-coefficient:
(q2-r2) (-p2+q2+r2)
Properties
- The major points on this line are: QA-P5, QA-P1, QA-P10, QA-P20 in this order with mutual distance-ratios 3 : 1 : 2 (see comments at QA-P10 and QA-P20).
- Major and minor points on this line are: QA-P5, QA-P25, QA-P1, QA-P26, QA-P10, QA-P22, QA-P20 in this order with mutual distance-ratios: 16 : 2 : 2 : 4 : 3 : 9.
- The barycentric coordinates of QA-L3 are algebraically independent of (a,b,c) just like all known points on this line: QA-P1, QA-P5, QA-P10, QA-P18, QA-P20, QA-P22, QA-P25, QA-P26.
- QA-L3 is the 5th Point tangent at QA-P1 and QA-P20. See QA-Tf9.
- QA-P22 is the Center of the QA-Line Involution (see QA-Tf1) on QA-L3.
- QA-Co5 is the Involutary Conjugate (see QA-Tf2) of QA-L3.
Estimated human page views: 652
