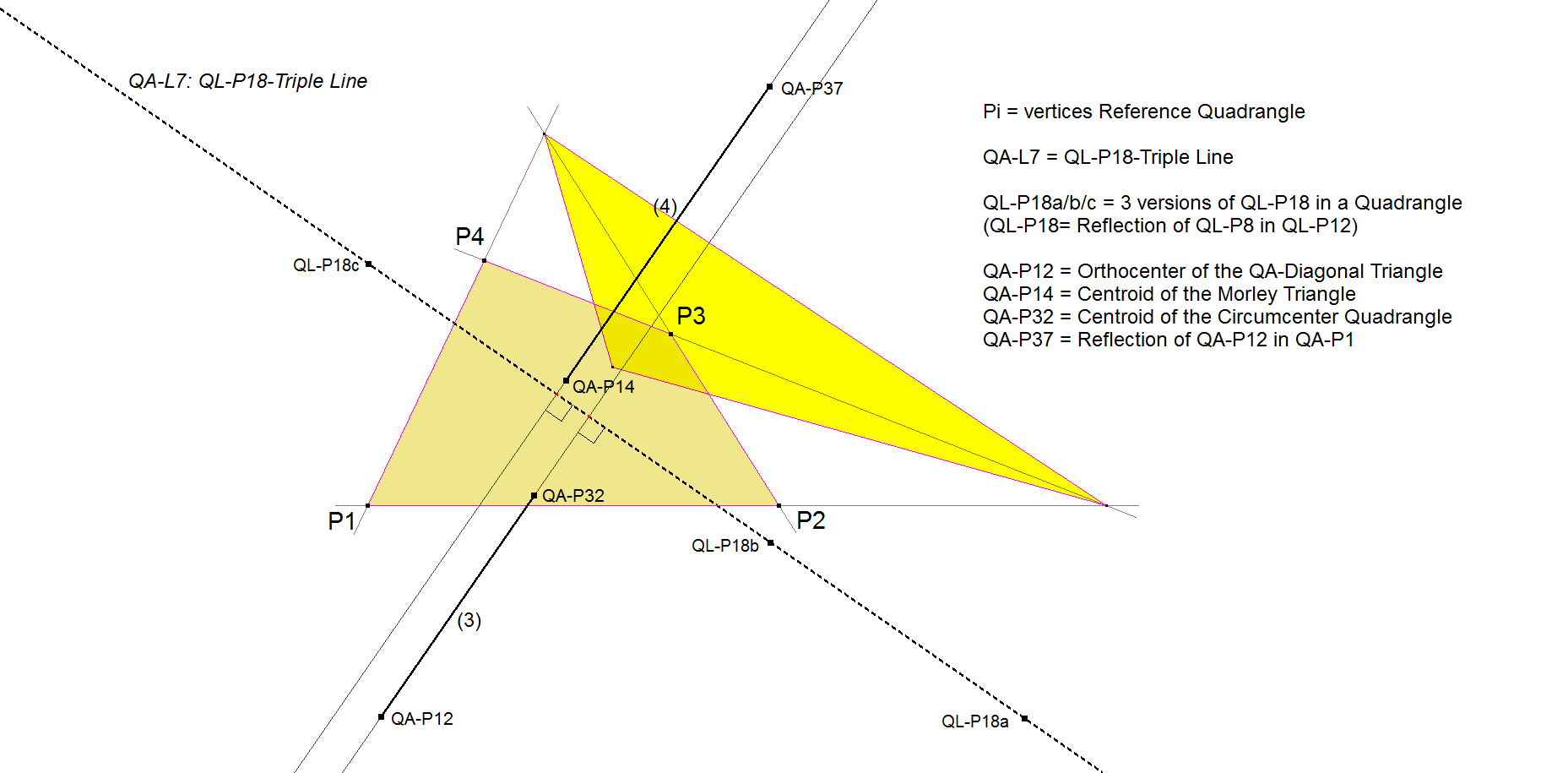
QA-L7: QL-P18-Triple Line
The 3 QA-versions of QL-P18 are collinear and determine the line QA-L7.
This line was found by Eckart Schmidt (November 29, 2012).
Further explanation about a Px-Triple Line can be found at QA-Tr-1.
1st CT-coefficient QA-L7:
-2 q2 r2 (q + r)2 + p4 (q2 + r2) + p q r (q + r) (q2 – 3 q r + r2)
+ p3 (q + r) (2 q2 + q r + 2 r2) + p2 (q4 + 4 q3 r + 4 q2 r2 + 4 q r3 + r4)
1st CT-coordinate Infinity point QA-L7:
p (q2 – r2) (3 p (p + q + r) – q r)
1st DT-coefficient QA-L7:
p4 (q2 + r2) + (q2 – r2)(-2p2 + q2 + r2).
1st DT-coordinate Infinity point QA-L7:
q2 – r2
Properties
- QA-L7 is perpendicular to QA-P12.QA-P32 and QA-P14.QA-P37.
- Special about these lines is that the ratio of the lengths of the line segments QA-P12.QA-P32 : QA-P14.QA-P37 = 3 : 4.
- QA-L7 is parallel to one of the asymptotes of the QA-DT circumscribed hyperbola which is the Involutary Conjugate of the line through QA-P22 and its Involutary Conjugate.
- QA-L7 is parallel to the Trilinear Polar of the QA-DT-Isotomic Conjugate of QA-P16 (Eckart Schmidt, November 29, 2012).
- QA-L7 is the QA-Tf2 image of a QA-DT circumscribed conic with its center in a point, that divides QA-P10.QA-P17 in the ratio -1/3 (Eckart Schmidt, November 29, 2012).
Estimated human page views: 556
