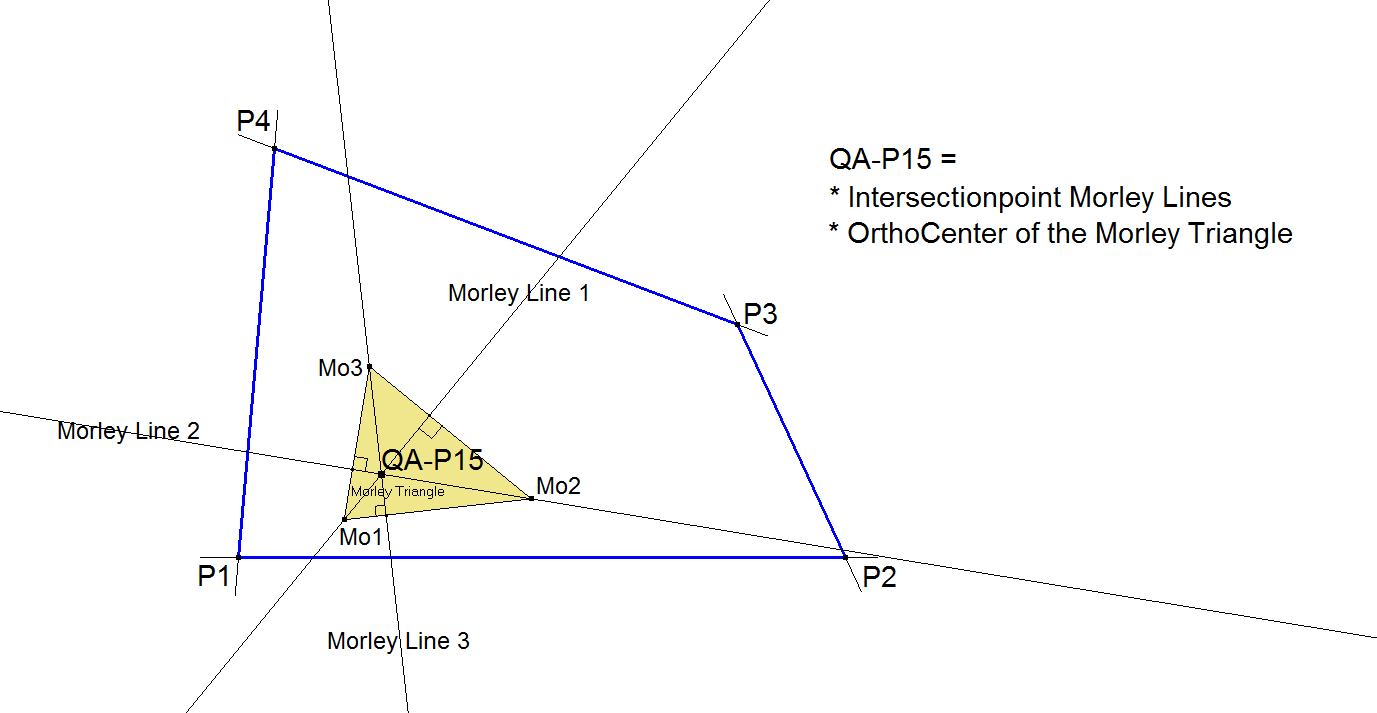
QA-P15: OrthoCenter of the Morley Triangle
The QL-Morley Points (QL-P2) of the 3 Quadrigons of the Reference Quadrangle form a triangle Mo1.Mo2.Mo3.
The QL-Morley Lines (QL-L4) of the 3 Quadrigons of the Reference Quadrangle pass through Mo1, Mo2, Mo3. So their common intersection point could be called the QA-OrthoPoint.
The QL-Morley Lines also happen to be the altitudes of the Morley Triangle.
So their common intersection point is also the OrthoCenter of the Morley Triangle.
1st CT-coordinate:
a4 (p + q) (p + r) (p (q2 + r2) + (q + r) (q2 + q r + r2))
-b4 (p + q) (q + r) (2 p3 + r (q + r)2 + p (q + r) (q + 3 r) + p2 (3 q + 5 r))
-c4 (p + r) (q + r) (2 p3 + q (q + r)2 + p (q + r) (3 q + r) + p2 (5 q + 3 r))
+a2 b2 (p + q) (2 p3 q + q r (q + r)2 + p r (q + r) (2 q + r) + p2 (2 q2 + 5 q r + r2))
+a2 c2 (p + r) (2 p3 r + q r (q + r)2 + p q (q + r) (2 r + q) + p2 (2 r2 + 5 q r + q2))
+b2 c2 (q + r) (4p4 + 10p3 (q + r) + 2q r (q + r)2 + p (q + r) (3q + r) (q + 3r) + p2 (9q2 + 22q r + 9r2))
1st DT-coordinate:
-2 SA2 p4 (p2 + q2 – r2) (p2 – q2 + r2) -SB2 q2 (3 (p2 – r2)3 – q2 (p2 – r2) (3 p2 + 5 r2)
– q4 (-p2 + q2 + r2)) -SC2 r2 (3 (p2 – q2)3 – (p2 – q2) (3 p2 + 5 q2) r2 – r4 (-p2 + q2 + r2))
+SB SC (-8 q2 r2 (2 p4 – p2 q2 – p2 r2 + 2 q2 r2) + (-p2 + q2 + r2)4)
-8 SA p4 (SB (p2 – q2) q2 + SC (p2 – r2) r2)+ S2 p2 (4 q2 r2 (p2 + q2 + r2) + (p2 – q2 – r2)3)
Properties:
- QA-P15 lies on the line QA-L6 (QA-Newton-Morley Line).
- QA-P15 is the common point of the 3 QA-versions of QL-L4 (Morley Line).
- The 3 QL-versions of QA-P15 are collinear and lie on QL-L4 (note Eckart Schmidt).
- QA-P15 is the circumcenter of the QG-P10 circle in the QA-environment (QG-P10=2nd Quasi Orthocenter) (note Eckart Schmidt).
- QA-P15 is the Orthocenter of the Triangle formed by the 3 QA-versions of QL-P2 (note Eckart Schmidt).
- QA-P15 is the Orthocenter of the Triangle formed by the 3 QA-versions of QG-P7 (note Eckart Schmidt).
- QA-P15 is the Perspector of the mutual Triple Triangles (see QA-Tr-1) of QL-P2, QL-P3, QL-P29.
- QA-P15 is the Orthology Center of the Triple Triangles of QL-P1/QL-P3/QL-P29 wrt the Triple triangles of QG-P5/QG-P10/QL-P2. See QA-Tr-1.
- QA-P15 is the Orthology Center of the QG-P7 Triple Triangle wrt the Triple triangles of QG-P9/QL-P6. See QA-Tr-1.
Estimated human page views: 580