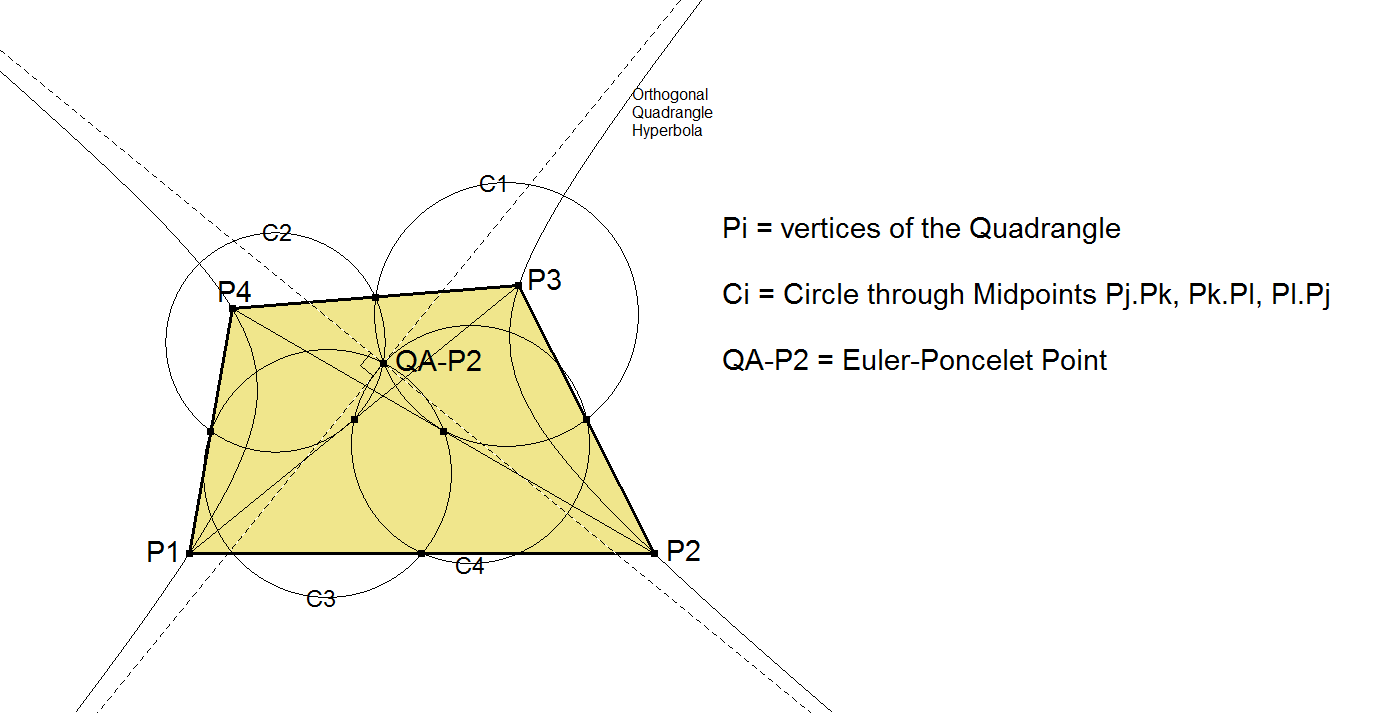
QA-P2: Euler-Poncelet Point

QA-P2: Euler-Poncelet Point

Euler mentioned this point in one of his numerous papers.

In 1821 Brianchon and Poncelet, both captains of artillery, wrote a book (Ref-1) in which the orthogonal hyperbola and this point were worked out.

The Euler-Poncelet Point can be defined in different ways.

1. It is the center of the orthogonal hyperbola through P1, P2, P3 and P4.

2. It is the common point of the Nine-point Circles of the triangles Pj.Pk.Pl for all combinations of (j,k,l) ∈ (1,2,3,4).

3. It is the common point of the Pedal Circles of points Pi wrt triangles Pj.Pk.Pl for all combinations of (i,j,k,l) ∈ (1,2,3,4).

This point is also described at Ref-2c, Ref-8, Ref-15f and Ref-42.

Coordinates:

1st CT-Coordinate:

p (S_B q - S_C r) (b²r (p+q) - c²q (p+r))

1st DT-Coordinate:

1/(b² r² - c² q²)

Properties:

QA-P2 lies on these QA-lines:

– QA-P1.QA-P3 (-1 : 2 => QA-P2 = Reflection of QA-P3 in QA-P1)

– QA-P4.QA-P6 (2 : -1 => QA-P2 = Reflection of QA-P4 in QA-P6)

– QA-P10.QA-P29 (-2 : 3 => QA-P2 = AntiCompl. of QA-P29 wrt QA-DT)

– QA-P11.QA-P30 (-1 : 2 => QA-P2 = Reflection of QA-P30 in QA-P11)

– QA-P12.QA-P36 (2 : -1 => QA-P2 = Reflection of QA-P12 in QA-P36)

QA-P2 is the center of the Orthogonal Hyperbola through P1, P2, P3, P4.
QA-P2 is the common point of Nine-point Circles Pi.Pj.Pk for all combinations of (j,k,l)∈ (1,2,3,4).
QA-P2 is the common point of the Pedal Circles of points Pi wrt triangles Pj.Pk.Pl for all combinations of (i,j,k,l) (1,2,3,4). See Ref-42.
QA-P2 is the point of concurrence of the four circles determined by the feet of the perpendiculars dropped from each of the four points onto the sides of the triangle formed by the other three. See Ref-13, Nine-point Circle. See Ref-8, Euler Cirkels. See also QA-P42.
QA-P2 is the Homothetic Center of the Antigonal Quadrangle and the Reference Quadrangle (the Antigonal of a point X isthe isogonal conjugate of the inverse in the circumcircle of the isogonal conjugate of X, see Ref-17a.
QA-P2 is the Midpoint of the reflections of QA-P4 in Pi.Pj and Pk.Pl (note Eckart Schmidt).
Let M = Diagonal Point Pi.Pj ^ Pk.Pl. Now M.QA-P4 and M.QA-P2 are symmetric wrt the angle bisector of lines Pi.Pj and Pk.Pl for all combinations of (i,j,k,l) ∈ (1,2,3,4). See Ref-16 page 8.
QA-P2 lies on the circumcircle of the QA-Diagonal Triangle.
QA-P2 lies on the circumcircles of triangles formed by the 3 QA-versions of QG-P1, QG-P6, QG-P10, QG-P14 as well as QG-P17.
QA-P2 lies on the Nine-point Conic (QA-Co1).
QA-P2 is concyclic with QA-P7, QA-P8 and QA-P23.
A Maltitude ("Midpoint altitude") is a perpendicular drawn to a side of a Quadrigon from the midpoint of the opposite side. The 2nd generation of the Maltitude Quadrigon is homothetic with the Reference Quadrigon. Let M be their perspector. M is the same point for each quadrigon in a Quadrangle and coincides with QA-P2.
Let Q1 be the isogonal conjugate of QA-P4 wrt P2P3P4, and define Q2, Q3, Q4 cyclically. The quadrangle Q1Q2Q3Q4 is homothetic to P1P2P3P4 at QA-P2 (Randy Hutson, July, 2012).
QA-P2 is also the Euler-Poncelet Point of the Orthocenter Quadrangle (Eckart Schmidt, August 24, 2012).
The circumcircles of the Euler Triangles (see Ref-13) of the Component Triangles concur in QA-P2 (Seiichi Kirikami, October 1, 2012).
QA-P2 is the Orthopole (see Ref-13) of line QA-P4.Pi wrt triangle Pj.Pk.Pl for all (i,j,k,l) ∈ (1,2,3,4). See Ref-11, Hyacinthos messages # 21865 & 21867.
Let O1, O2, O3, O4 be the circumcenters of the Component Triangles of Reference Quadrangle P1.P2.P3.P4. Let OPi be the Orthopole of line P.Oi (P=random point) wrt Component Triangle Pj.Pk.Pl, where (i,j,k,l) ∈ (1,2,3,4). The 4 Orthopoles OP1, OP2, OP3, OP4 are concyclic on a circle through QA-P2. See Ref-11, Hyacinthos messages # 21865 & 21867.
QA-P2 is the QA-Orthopole (QA-Tf3) of QA-P4. The QA-Orthopole of QA-P2 is QA-P23.
The QA-Möbius Conjugate (QA-Tf4) of QA-P2 is a point on the line QA-P4.QA-P41 and is the Midpoint of (QA-P4,QA-Tf4(QA-P6)).
Let Nij be the feet of the perpendiculars from QA-P4 to Pi.Pj. Then the 4 versions of circles through Nij, Njk, Nki (for all combinations (i,j,k,l) ∈ (1,2,3,4)) have one common point, which is QA-P2 (Seiichi Kirikami, July 17, 2013). See Ref-34, Quadri-Figures-Group, message # 126.
If the Reference Quadrangle is cyclic, then QA-P2 is its Anticenter. See Ref-13 (Seiichi Kirikami, November 6, 2013).
In a cyclic Quadrangle QA-P2 is the Complement wrt Triangle Pj.Pk.Pl of the reflection of Pi in QA-P4. See Ref-34. QFG #972.
QA-P2 is the Cyclologic Center of the QG-P1-Triple Triangle wrt the QG-P15-Triple Triangle. See Ref-34, QFG #965, #966.
QA-P2 is the Orthology Center of the QG-P15 Triple Triangle wrt the Triple Triangles of QG-P7/QG-P9/QL-P6. See QA-Tr-1.
QA-P2 is the Parallelologic Center of the QG-P10 Triple Triangle wrt the Triple Triangles of QG-P7/QG-P9/QL-P6 TT. See QA-Tr-1.

MATHEMATICS

Plaats reactie