QA-P5: Isotomic Center
The Isotomic Center is the Perspector of the Reference Quadrangle with the Isotomic Conjugate Quadrangle.
Stated in another way:
The Isotomic Center is the common intersection point of lines Pi.Qi, where
- Pi = ith quadrangle vertice,
- Qi = Isotomic Conjugate of Pi wrt Pj.Pk.Pl
for all permutations of (i,j,k,l) ∈ (1,2,3,4).
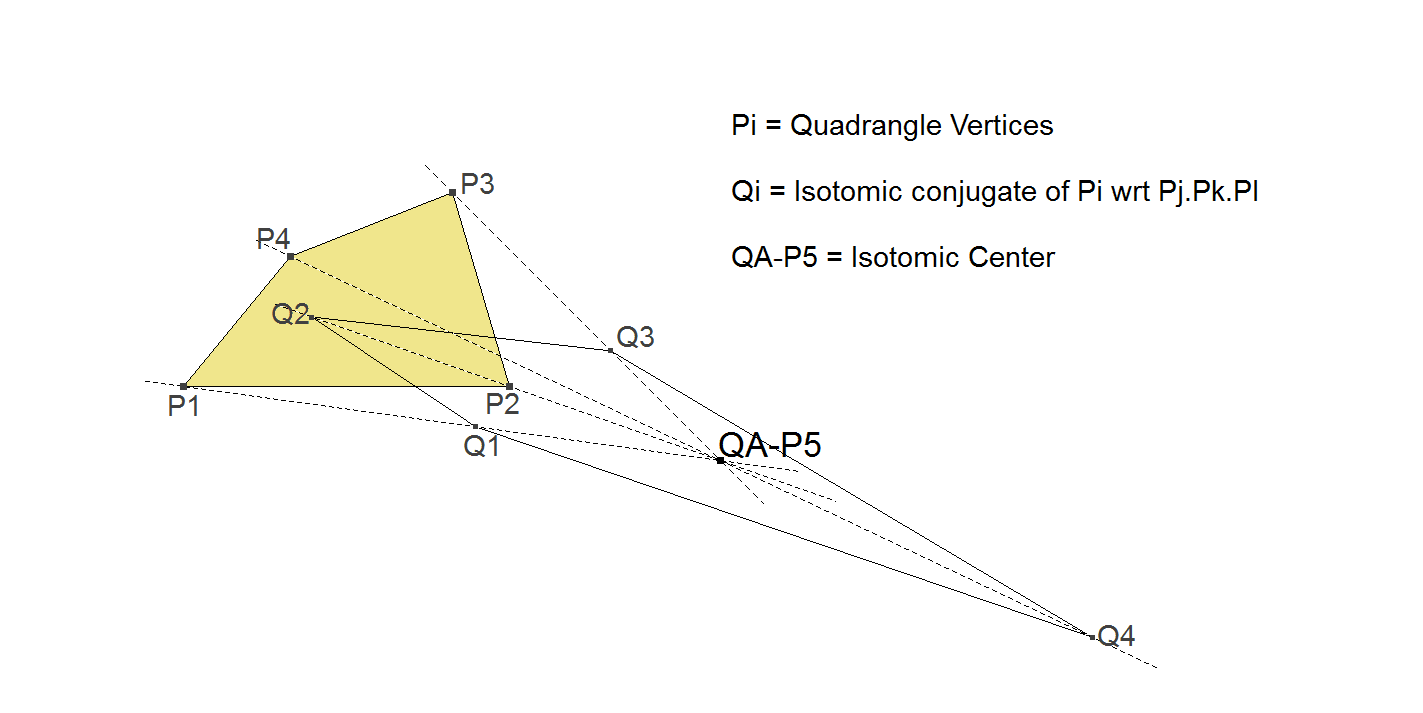
Construction:
Coordinates:
1st CT-Coordinate:
q r (q+r) (2p+q+r) (note that this formula is independent of a,b,c)
1st DT-Coordinate:
-4 (p4 + q2 r2) + (p2 + q2 + r2)2
Properties:
- QA-P5 lies on these QA-lines:
- QA-P5 lies on these QG-lines:
- QA-P5 is the Reflection of:
- QA-P5 is the AntiComplement of QA-P20 wrt the QA-Diagonal Triangle.
- QA-P5.QA-P1 : QA-P1.QA-P10 : QA-P10.QA-P20 = 3 : 1 : 2.
- QA-P5 forms with the vertices of the QA-Diagonal Triangle a quadrangle that shares the same centroid with the Reference Quadrangle.
- QA-P5 is the QA-Involutary Conjugate (see QA-Tf2) of QA-P17.
- QA-P5 lies on the Conic through P1, P2, P3, P4 and QA-P10.
- QA-P5 lies on the Cubics QA-Cu2 and QA-Cu4.
-
Given Bimedians M12*M34, M13*M24, M14*M23 of the Reference Quadrangle. Let T1.T2.T3 be the AntiComplementary Triangle of the Diagonal Triangle S1.S2.S3. The corresponding lines parallel to the Bimedians through T1, T2 and T3 concur in QA-P5 (Seiichi Kirikami, September 30, 2012).
-
QA-P5 is the center of the circle of points where: sum of quadratic distances to Quadrangle - vertices = sum of quadratic distances to DT - vertices.
- QA-P5 is the Perspector of the Triple Triangles (see QA-Tr-1) of these pairs (QG-P2, QG-P4), (QG-P14, QL-P15).