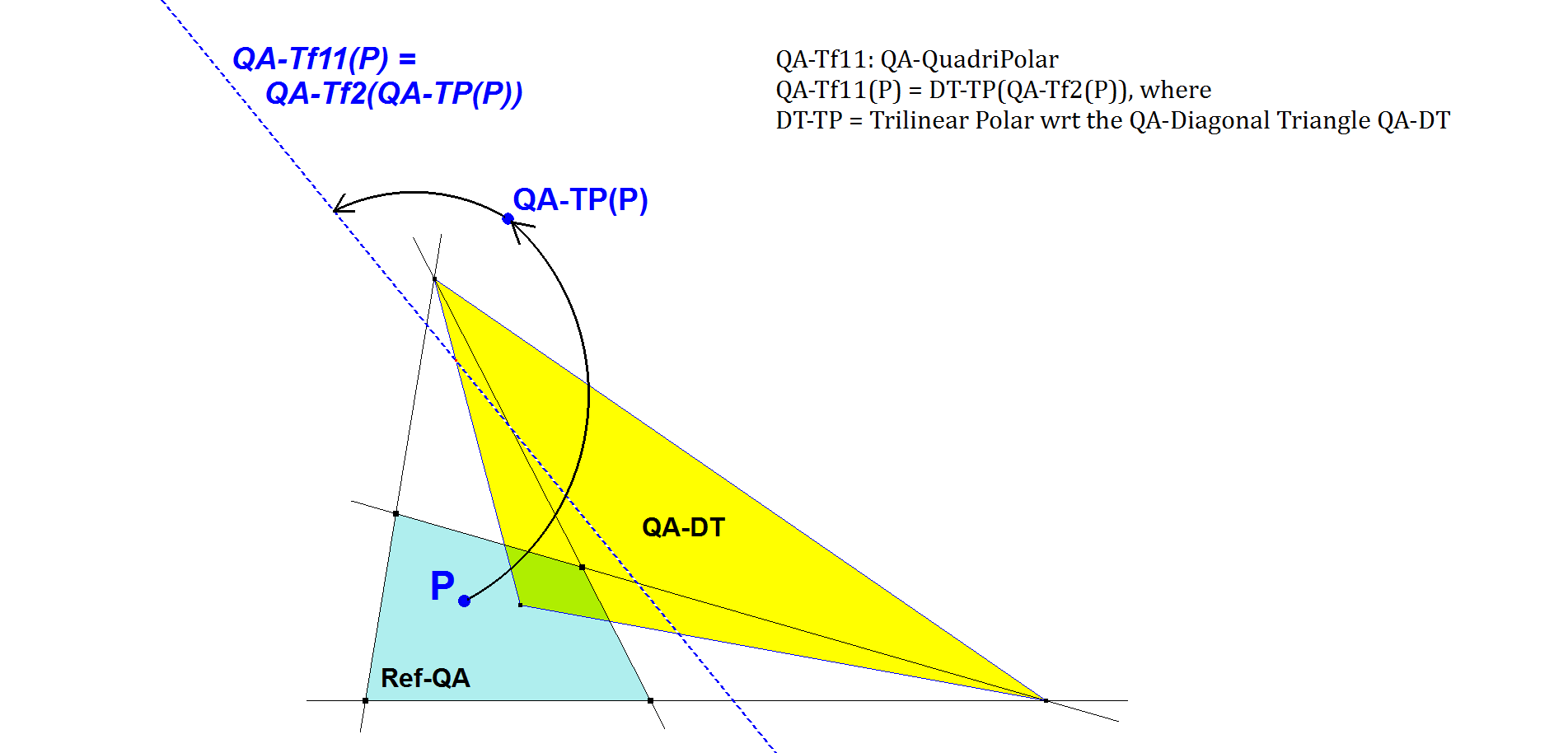
QA-Tf11: QA-QuadriPolar
The QA-QuadriPolar is an equivalent of the Tripolar (also named Trilinear Polar) in a triangle. It transforms in a Quadrangle “harmonically” a point into a line.
QA-Tf11(P) = DT-TP(QA-Tf2(P)), where DT-TP = Trilinear Polar wrt the QA-Diagonal Triangle QA-DT (=QA-Tr1).
The combination QA-Tf10/QA-Tf11 in a Quadrangle is the equivalent of the combination QL-Tf10/QL-Tf11 in a Quadrilateral.
In particular QA-Tf11 is the dual of QL-Tf10 and has the same coordinates as QL-Tf10 when substituting (l:m:n) > (p:q:r).
CT-coordinates
Let P = (x:y:z), then QA-Tf11(P) =
(q r (-3 q r x + p r y + p q z) : p r (q r x – 3 p r y + p q z) : p q (q r x + p r y – 3 p q z))
DT-coordinates
Let P = (x:y:z), then QA-Tf11(P) =
(x/p2 : y/q2 : z/r2)
Properties
- QA-Tf11(QA-Tf10(L)) = L and QA-Tf10(QA-Tf11(P)) = P.
- QA-Tf11(P) also can be obtained as QL-Tf2*( DT-Tripolar(P)),
- where QL-Tf2* = QL-Tf2-transformation wrt the dual QL with defining lines Li = DT-Tripolar(Pi) (i=1,2,3,4). Therefore it is also QL-Tf11(P) wrt the dual QL. See QA-8.
Estimated human page views: 394
