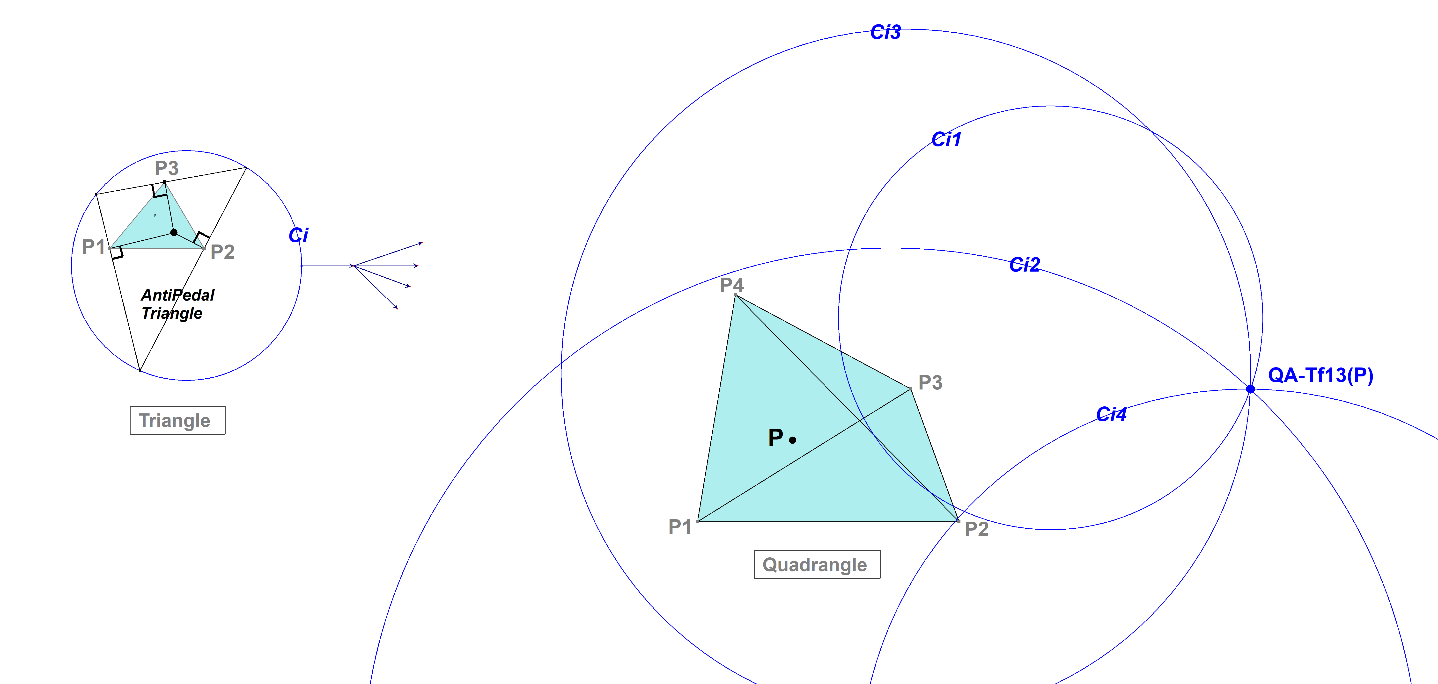
QA-Tf13: QA-AntiPedal Point
Definition: The AntiPedal triangle of P wrt a reference triangle ABC is the triangle of which ABC is the Pedal Triangle of P (see QA-Tf12). The vertices of the AntiPedal Triangle are called the AntiPedal Points.
The QA-AntiPedal Point is defined as follows.
• The 3 AntiPedal Points of P wrt a Triangle define a AntiPedal Circle Ci.
• In a Quadrangle the 4 AntiPedal Circles Ci (denoted as Ci1, Ci2, Ci3, Ci4) of the Component Triangles intersect at a common point being the QA-AntiPedal Point.
This transformation is mentioned first at Ref-34, QFG#1223.
See also Ref-34, QFG-message #2759 for a generalization to n-Points.
• The 3 AntiPedal Points of P wrt a Triangle define a AntiPedal Circle Ci.
• In a Quadrangle the 4 AntiPedal Circles Ci (denoted as Ci1, Ci2, Ci3, Ci4) of the Component Triangles intersect at a common point being the QA-AntiPedal Point.
This transformation is mentioned first at Ref-34, QFG#1223.
See also Ref-34, QFG-message #2759 for a generalization to n-Points.
1st CT-coordinate of QA-Tf13[(x:y:z)]:
Formula of the 15th degree. Too long and too complicated to be mentioned here.
Properties:
• QA-P4 is transformed into QA-P9. See Ref-34, QFG#1223.
• When P is any point on a Circumscribed Circle of a QA-Component Triangle, then QA-Tf13(P) will be the point diametrically to P on that circle.
• QA-Tf13 can be generalized as the transformation nP-e-Tf2 in an n-Point (system of n reference points). It matches with nP-e-Tf2 when n=4. See Ref-34, QFG#2759.