QA-Tf16: QA-Keizer-Schmidt Conjugate
This special Conjugate was found by Bernard Keizer and Eckart Schmidt as a byproduct searching for the background of 5 mysterious points, being the 5 common points of the 3 QL-versions of the cubic QA-Cu7.
See [34], QFG-messages #3260, #3261, #3265, #3268, #3270, #3276-#3279, #3281.
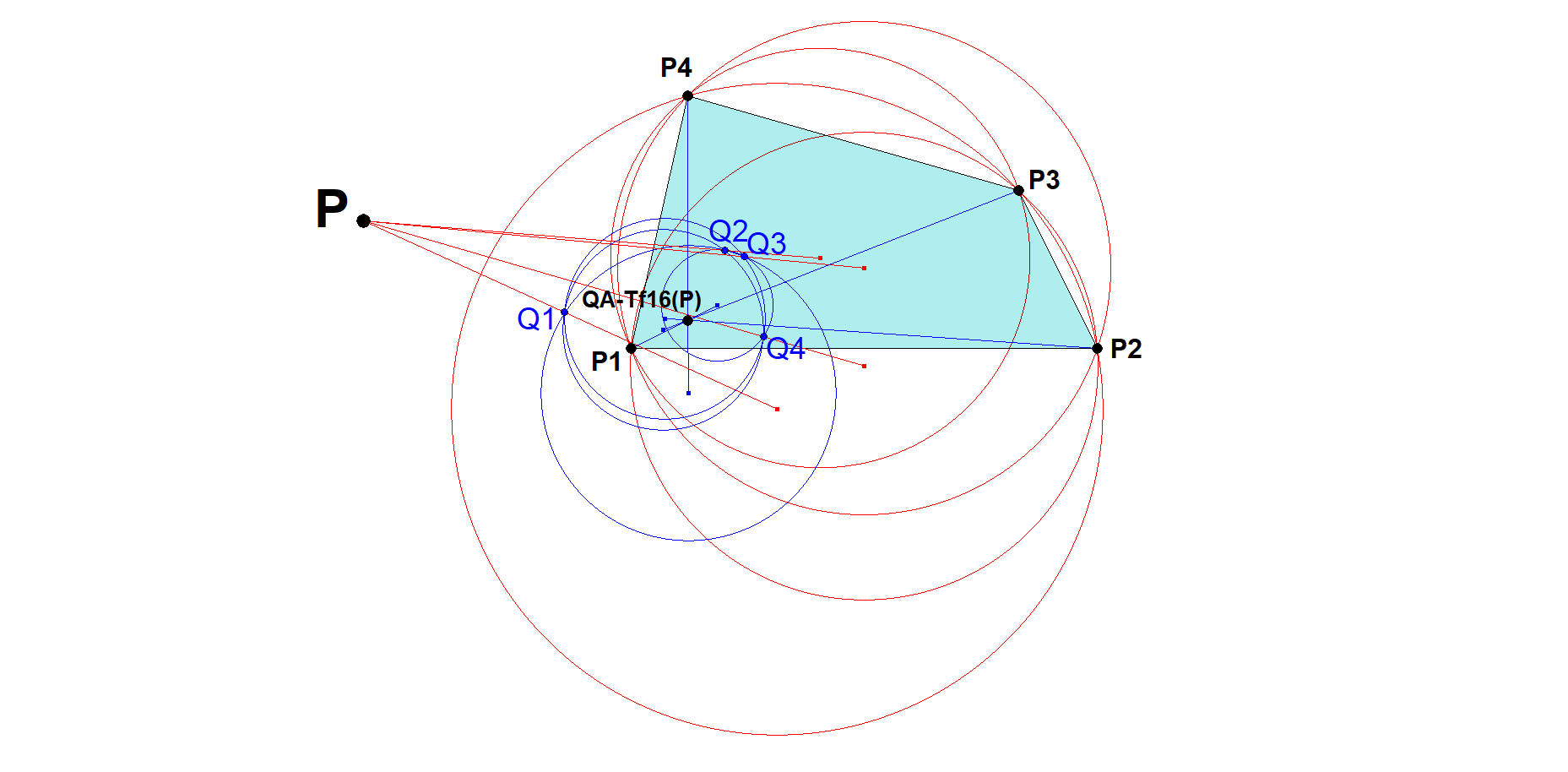
Given a Reference Quadrangle P1.P2.P3.P4 and a random point P.
- Let Q1 be the inverse of P wrt Circle (P2, P3, P4).
- Let Q2 be the inverse of P wrt Circle (P3, P4, P1).
- Let Q3 be the inverse of P wrt Circle (P4, P1, P2).
- Let Q4 be the inverse of P wrt Circle (P1, P2, P3).
Then QA-Tf16(P) =
- the inverse of P1 wrt the circle (Q2, Q3, Q4),
- the inverse of P2 wrt the circle (Q3, Q4, Q1),
- the inverse of P3 wrt the circle (Q4, Q1, Q2),
- the inverse of P4 wrt the circle (Q1, Q2, Q3).
First CT-coordinate of QA-Tf16[(x:y:z)]
(a4 (p + q) (p + r) y z – b4 p (p + q) x z – c4 p (p + r) x y + b2 c2 p x ((p + q + r) x + r y + q z) + a2 b2 (p + q) (p x + r x – p y) z + a2 c2 (p + r) y (p x + q x – p z)) /
(a2 (p y z (p + q + r) – q r x (x + y + z)) + b2 p x (z (p + q) – r (x + y)) + c2 p x (y (p + r ) – q (x + z)))
Properties
- QA-Tf16(QA-Tf16(P)) = P.
- QA-Tf16(QA-P41) lies on the line QA-P3.QA-P41. See [34], QFG#3276.
- QA-Tf16(QA-P3) as well as QA-Tf16(QA-P41) lie on the cubic QA-Cu1. See [34], QFG#3276.
- QA-Cu1 is invariant under the QA-Tf16 transformation. See [34], QFG#3277.
- For P on QA-Cu1 it holds that P, QA-Tf16(P), 5P-s-P4(P1,P2,P3,P4, P) and QA-P3 are collinear. See [34], QFG#3283.
- QA-Tf16 maps the Diagonal Triangle QA-Tr1 to the Miquel Triangle QA-Tr2 and vice versa. See [34], QFG#3277.
Estimated human page views: 320
