QA-Tf4: QA-Möbius Conjugate
A Möbius Transformation transforms generalized circles into generalized circles. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
However it preserves the angles between the intersection of circles. See Ref-35.
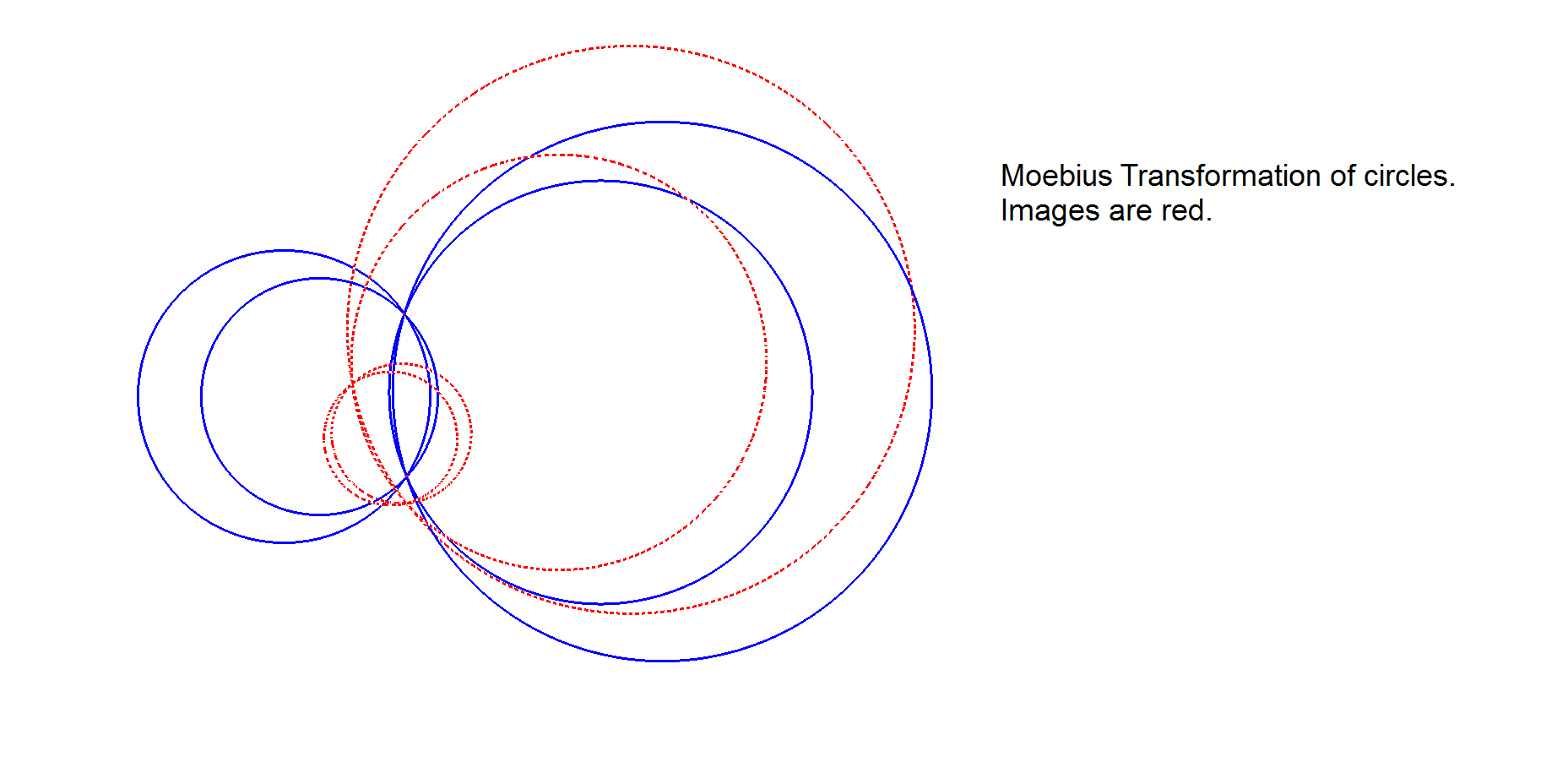
In a strictly geometric way we define here the Möbius Conjugate as follows.
Given a circle Ci and an axis Ax through the center of Ci. The Möbius Conjugate is defined here as the Reflection in Ax of the Inverse wrt Ci of some point P.
It also could be defined as the Inverse wrt Ci of the Reflection in Ax of that same point P, since it gives the same result. Applying the Möbius Conjugate twice results in the point of origin.
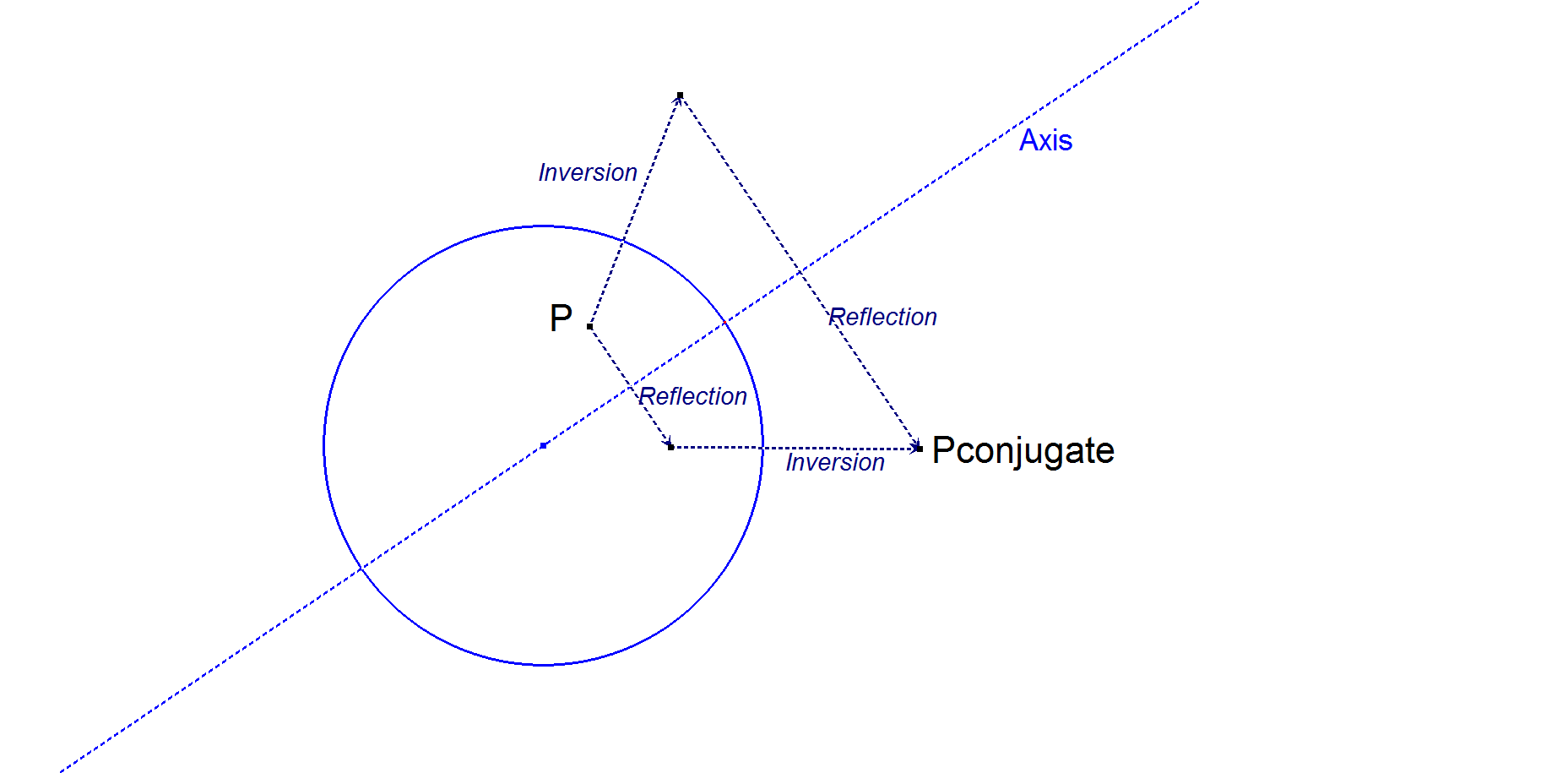
This Möbius Conjugate occurs also in Quadrangle Geometry and Quadrilateral Geometry.
In Quadrilateral Geometry we have QL-Tf1, the Clawson-Schmidt Conjugate with QL-P1 as the circle center.
In Quadrangle Geometry we here have QA-Tf4, which is called the QA-Möbius Conjugate.
It comes forward from a property from QA-P4 that the angle bisectors of Pi.QA-P4.Oi (i=1,2,3,4) coincide, where Oi = Circumcenter (Pj,Pk,Pl) and where (i,j,k,l) ∈ (1,2,3,4).
This Angle bisector is the Axis of the QA-Möbius Conjugate. The circle of this QA-Möbius Conjugate is the circle with center QA-P4 and squared radius = |QA-P4.Pi|.|QA-P4.Oi|, which has the same values for i=1,2,3,4.
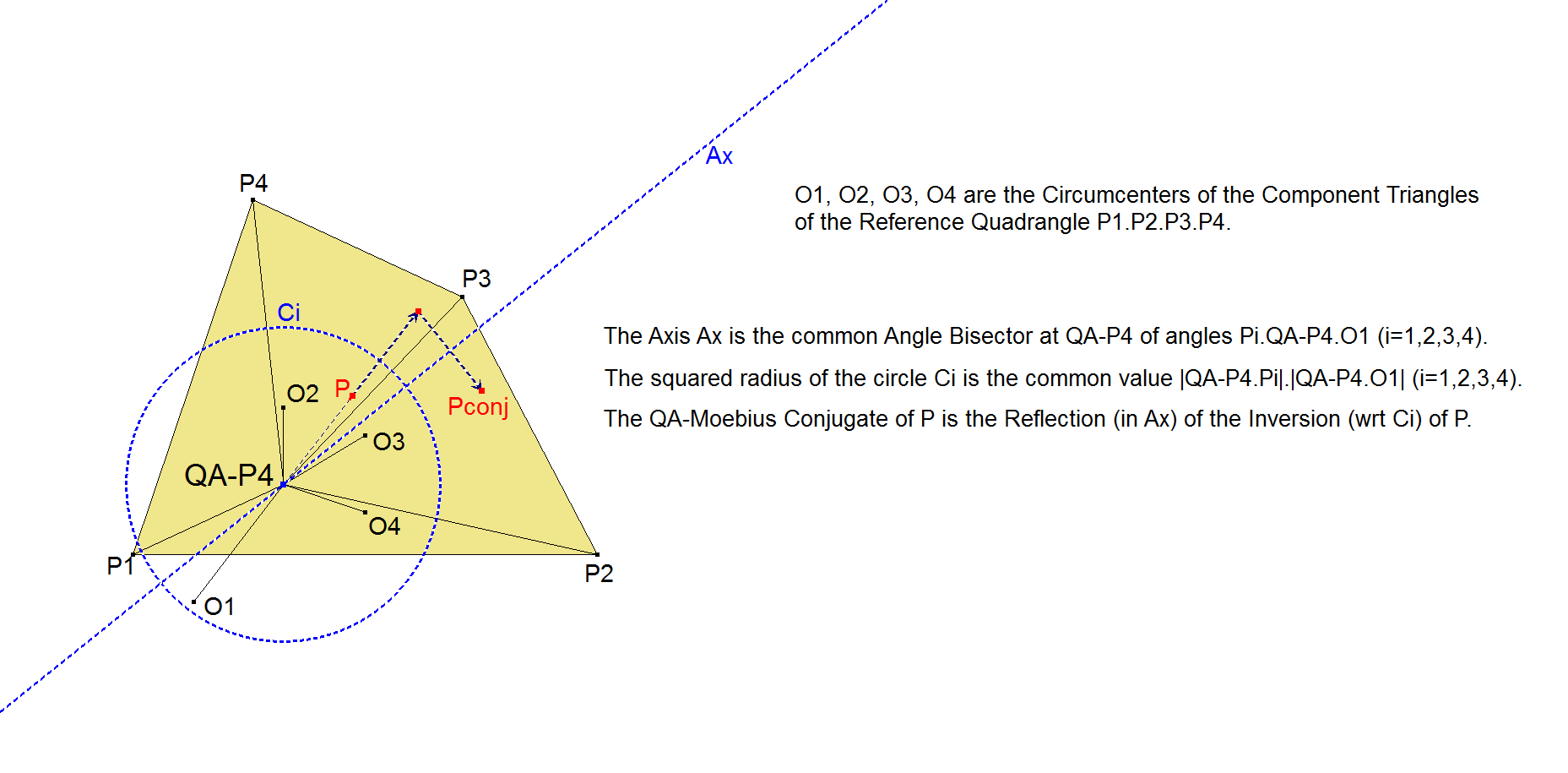
The QA-Möbius Conjugate was discovered and mentioned as "T-Inversion" with a simple construction method in a not published paper of Eckart Schmidt in 2000.
Seperately about at the same time the QA-Möbius Conjugate also was discovered by Benedetto Scimemi. Later on he published it. See Ref-36, page 341.
The coordinates of the image are not very simple and of the second degree.
However somehow this conjugate relates quite a lot of Quadri-points.
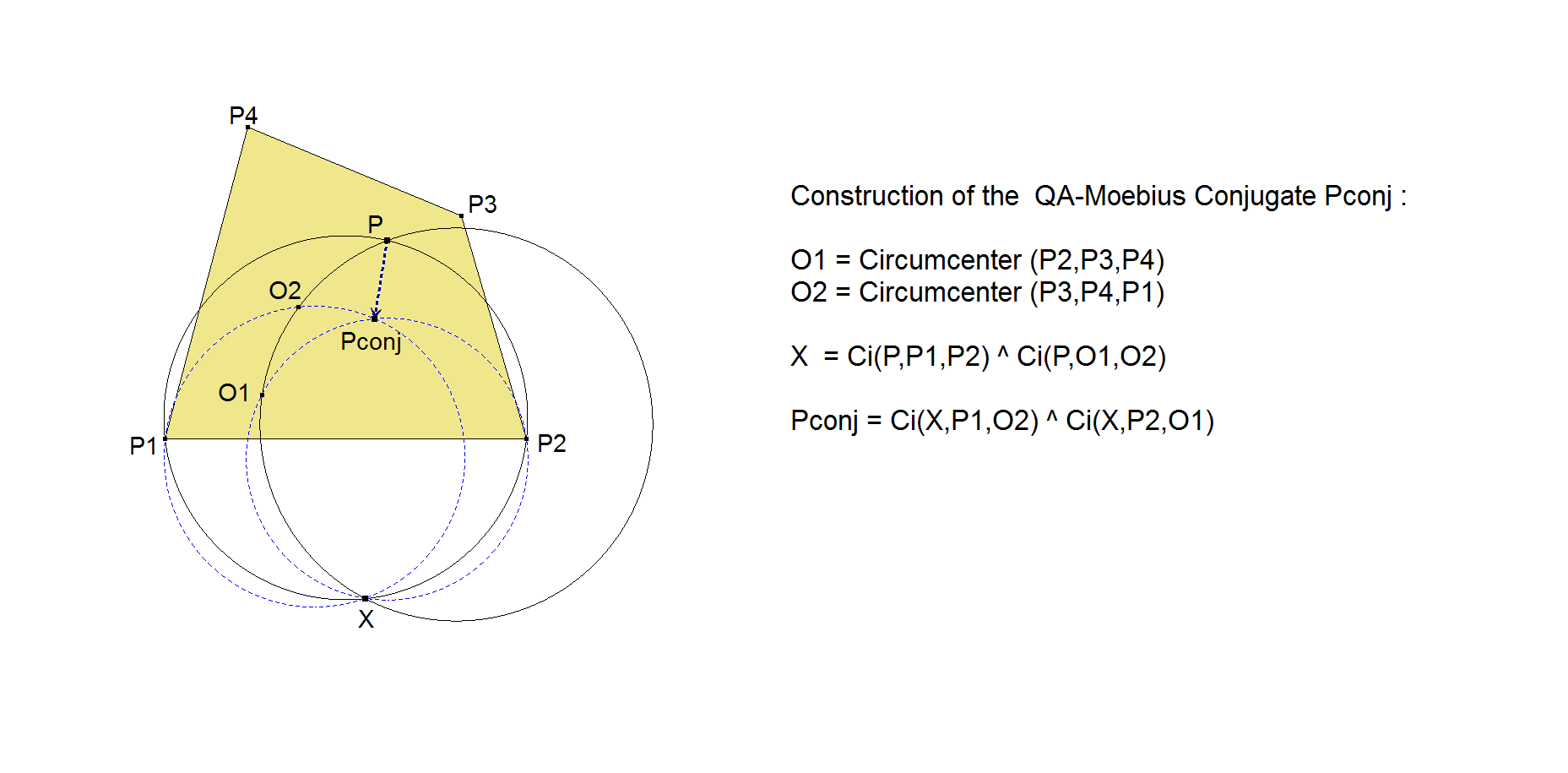
Here is a way of constructing the QA-Möbius Conjugate:
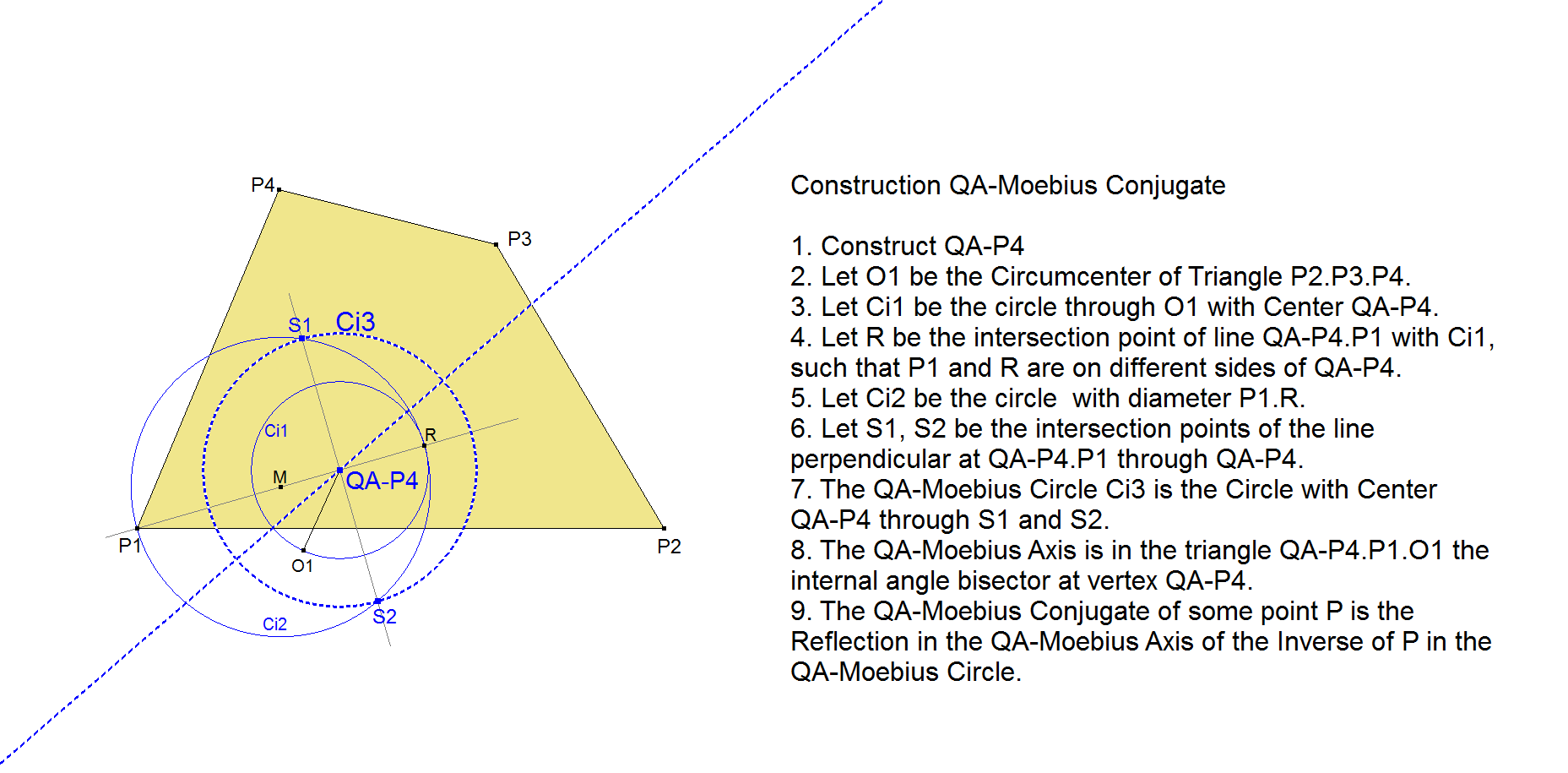
There is another surprisingly simple construction described by Eckart Schmidt (unpublished paper, 2000) without the use of QA-P4, its circle and its axis.
Transformation:
1st CT-Coordinate of the QA-Tf4 image of P(x:y:z):
-b2 c2 p (c2 q2 - a2 q r + b2 q r + c2 q r + b2 r2) (-a2 p2 + b2 p2 + c2 p2 - a2 p q + b2 p q - c2 p q - a2 p r - b2 p r + c2 p r - 2 a2 q r) x2
+c2 q (c2 p2 + a2 p r - b2 p r + c2 p r + a2 r2) (a4 p q - a2 b2 p q - 2 a2 c2 p q - b2 c2 p q + c4 p q + a4 q2 - a2 b2 q2 - a2 c2 q2 - a2 b2 p r - b4 p r + b2 c2 p r - 2 a2 b2 q r) y2
+b2 r (b2 p2 + a2 p q + b2 p q - c2 p q + a2 q2) (-a2 c2 p q + b2 c2 p q - c4 p q + a4 p r - 2 a2 b2 p r + b4 p r - a2 c2 p r - b2 c2 p r - 2 a2 c2 q r + a4 r2 - a2 b2 r2 - a2 c2 r2) z2
+(a4 c4 p3 q2 - a2 b2 c4 p3 q2 - 2 a2 c6 p3 q2 - b2 c6 p3 q2 + c8 p3 q2 + a4 c4 p2 q3 - a2 b2 c4 p2 q3 - a2 c6 p2 q3 - a8 p3 q r + 3 a6 b2 p3 q r - 3 a4 b4 p3 q r + a2 b6 p3 q r + 3 a6 c2 p3 q r - 2 a4 b2 c2 p3 q r - 2 a2 b4 c2 p3 q r + b6 c2 p3 q r - 3 a4 c4 p3 q r - 2 a2 b2 c4 p3 q r - 2 b4 c4 p3 q r + a2 c6 p3 q r + b2 c6 p3 q r - 2 a8 p2 q2 r + 6 a6 b2 p2 q2 r - 6 a4 b4 p2 q2 r + 2 a2 b6 p2 q2 r + 6 a6 c2 p2 q2 r - 5 a4 b2 c2 p2 q2 r - 2 a2 b4 c2 p2 q2 r + b6 c2 p2 q2 r - 5 a4 c4 p2 q2 r - 2 a2 b2 c4 p2 q2 r - b4 c4 p2 q2 r - b2 c6 p2 q2 r + c8 p2 q2 r - a8 p q3 r + 3 a6 b2 p q3 r - 3 a4 b4 p q3 r + a2 b6 p q3 r + 3 a6 c2 p q3 r - 3 a4 b2 c2 p q3 r - a4 c4 p q3 r - a2 c6 p q3 r + a4 b4 p3 r2 - 2 a2 b6 p3 r2 + b8 p3 r2 - a2 b4 c2 p3 r2 - b6 c2 p3 r2 - 2 a8 p2 q r2 + 6 a6 b2 p2 q r2 - 5 a4 b4 p2 q r2 + b8 p2 q r2 + 6 a6 c2 p2 q r2 - 5 a4 b2 c2 p2 q r2 - 2 a2 b4 c2 p2 q r2 - b6 c2 p2 q r2 - 6 a4 c4 p2 q r2 - 2 a2 b2 c4 p2 q r2 - b4 c4 p2 q r2 + 2 a2 c6 p2 q r2 + b2 c6 p2 q r2 - 3 a8 p q2 r2 + 8 a6 b2 p q2 r2 - 7 a4 b4 p q2 r2 + 2 a2 b6 p q2 r2 + 8 a6 c2 p q2 r2 - 4 a4 b2 c2 p q2 r2 - 2 a2 b4 c2 p q2 r2 - 7 a4 c4 p q2 r2 - 2 a2 b2 c4 p q2 r2 + 2 a2 c6 p q2 r2 - a8 q3 r2 + 2 a6 b2 q3 r2 - a4 b4 q3 r2 + 3 a6 c2 q3 r2 - a4 b2 c2 q3 r2 - 2 a4 c4 q3 r2 + a4 b4 p2 r3 - a2 b6 p2 r3 - a2 b4 c2 p2 r3 - a8 p q r3 + 3 a6 b2 p q r3 - a4 b4 p q r3 - a2 b6 p q r3 + 3 a6 c2 p q r3 - 3 a4 b2 c2 p q r3 - 3 a4 c4 p q r3 + a2 c6 p q r3 - a8 q2 r3 + 3 a6 b2 q2 r3 - 2 a4 b4 q2 r3 + 2 a6 c2 q2 r3 - a4 b2 c2 q2 r3 - a4 c4 q2 r3) y z
+c2 (a4 c2 p3 q2 - b4 c2 p3 q2 - 2 a2 c4 p3 q2 - 2 b2 c4 p3 q2 + c6 p3 q2 + a4 c2 p2 q3 - b4 c2 p2 q3 - a2 c4 p2 q3 + b2 c4 p2 q3 - a6 p3 q r + 2 a4 b2 p3 q r - a2 b4 p3 q r + 3 a4 c2 p3 q r - a2 b2 c2 p3 q r - 4 b4 c2 p3 q r - 3 a2 c4 p3 q r - b2 c4 p3 q r + c6 p3 q r - a6 p2 q2 r + 3 a4 b2 p2 q2 r - 3 a2 b4 p2 q2 r + b6 p2 q2 r + 4 a4 c2 p2 q2 r - 3 a2 b2 c2 p2 q2 r - b4 c2 p2 q2 r - 5 a2 c4 p2 q2 r - 2 b2 c4 p2 q2 r + 2 c6 p2 q2 r + a4 b2 p q3 r - 2 a2 b4 p q3 r + b6 p q3 r + 2 a4 c2 p q3 r + 2 a2 b2 c2 p q3 r - 2 b4 c2 p q3 r - 2 a2 c4 p q3 r + b2 c4 p q3 r + a2 b4 p3 r2 - b6 p3 r2 - b4 c2 p3 r2 - 2 a6 p2 q r2 + 3 a4 b2 p2 q r2 - 3 a2 b4 p2 q r2 + 2 b6 p2 q r2 + 6 a4 c2 p2 q r2 - b4 c2 p2 q r2 - 6 a2 c4 p2 q r2 - 3 b2 c4 p2 q r2 + 2 c6 p2 q r2 - 2 a6 p q2 r2 + 2 a4 b2 p q2 r2 - a2 b4 p q2 r2 + b6 p q2 r2 + 5 a4 c2 p q2 r2 + a2 b2 c2 p q2 r2 - b4 c2 p q2 r2 - 4 a2 c4 p q2 r2 - b2 c4 p q2 r2 + c6 p q2 r2 + a4 b2 q3 r2 - a2 b4 q3 r2 + a4 c2 q3 r2 + 2 a2 b2 c2 q3 r2 - a2 c4 q3 r2 + a2 b4 p2 r3 + b6 p2 r3 - b4 c2 p2 r3 - a6 p q r3 + a4 b2 p q r3 + 3 a4 c2 p q r3 + a2 b2 c2 p q r3 + b4 c2 p q r3 - 3 a2 c4 p q r3 - 2 b2 c4 p q r3 + c6 p q r3 - a6 q2 r3 - a2 b4 q2 r3 + 2 a4 c2 q2 r3 + 2 a2 b2 c2 q2 r3 - a2 c4 q2 r3) x y
+b2 (a2 c4 p3 q2 - b2 c4 p3 q2 - c6 p3 q2 + a2 c4 p2 q3 - b2 c4 p2 q3 + c6 p2 q3 - a6 p3 q r + 3 a4 b2 p3 q r - 3 a2 b4 p3 q r + b6 p3 q r + 2 a4 c2 p3 q r - a2 b2 c2 p3 q r - b4 c2 p3 q r - a2 c4 p3 q r - 4 b2 c4 p3 q r - 2 a6 p2 q2 r + 6 a4 b2 p2 q2 r - 6 a2 b4 p2 q2 r + 2 b6 p2 q2 r + 3 a4 c2 p2 q2 r - 3 b4 c2 p2 q2 r - 3 a2 c4 p2 q2 r - b2 c4 p2 q2 r + 2 c6 p2 q2 r - a6 p q3 r + 3 a4 b2 p q3 r - 3 a2 b4 p q3 r + b6 p q3 r + a4 c2 p q3 r + a2 b2 c2 p q3 r - 2 b4 c2 p q3 r + b2 c4 p q3 r + a4 b2 p3 r2 - 2 a2 b4 p3 r2 + b6 p3 r2 - 2 b4 c2 p3 r2 - b2 c4 p3 r2 - a6 p2 q r2 + 4 a4 b2 p2 q r2 - 5 a2 b4 p2 q r2 + 2 b6 p2 q r2 + 3 a4 c2 p2 q r2 - 3 a2 b2 c2 p2 q r2 - 2 b4 c2 p2 q r2 - 3 a2 c4 p2 q r2 - b2 c4 p2 q r2 + c6 p2 q r2 - 2 a6 p q2 r2 + 5 a4 b2 p q2 r2 - 4 a2 b4 p q2 r2 + b6 p q2 r2 + 2 a4 c2 p q2 r2 + a2 b2 c2 p q2 r2 - b4 c2 p q2 r2 - a2 c4 p q2 r2 - b2 c4 p q2 r2 + c6 p q2 r2 - a6 q3 r2 + 2 a4 b2 q3 r2 - a2 b4 q3 r2 + 2 a2 b2 c2 q3 r2 - a2 c4 q3 r2 + a4 b2 p2 r3 - a2 b4 p2 r3 + b4 c2 p2 r3 - b2 c4 p2 r3 + 2 a4 b2 p q r3 - 2 a2 b4 p q r3 + a4 c2 p q r3 + 2 a2 b2 c2 p q r3 + b4 c2 p q r3 - 2 a2 c4 p q r3 - 2 b2 c4 p q r3 + c6 p q r3 + a4 b2 q2 r3 - a2 b4 q2 r3 + a4 c2 q2 r3 + 2 a2 b2 c2 q2 r3 - a2 c4 q2 r3) x z
Examples of QA-Möbius Conjugates:
|
Point/Line/Curve
|
QA-Tf4 - image
|
|
GENERAL
|
|
|
Defining Quadrangle Points: P1,P2,P3,P4
|
Circumcenters O1, O2, O3, O4 of the corresponding QA-Component Triangle
|
|
The vertices of the Diagonal Triangle QA-Tr1 of the Reference Quadrangle
|
The vertices of the Miquel Triangle QA-Tr2 of the Quadrangle O1.O2.O3.O4
(Eckart Schmidt, 2000)
|
|
A line not through QA-P4
|
A circle through QA-P4
|
|
A line through QA-P4
|
A line through QA-P4
|
|
A circle with QA-P4 as center
|
Another circle with QA-P4 as center
|
|
A circle not through QA-P4
|
Another circle not through QA-P4
|
|
A circle through QA-P4
|
A line not through QA-P4
|
|
|
|
|
SPECIFIC
|
|
|
QA-P4: Isogonal Center
|
Some (undefined) point at infinity
|
|
QA-P2: Euler-Poncelet Point
|
(suffix * means “QA-Möbius Conjugate of”)
|
|
QA-P3: Gergonne-Steiner Point
|
QA-P9: QA-Miquel Center
|
|
QL-P1: Miquel Point
|
QG-P5: 1st QG-Quasi Circumcenter
|
Collinearities:
(suffix * means “QA-Möbius Conjugate of”)
Other Properties:
- The Reflection Axis of the Conjugate is:
- Let Q1 and Q2 be two points collinear with QA-P4. Let Q1* and Q2* be their respective QA-Möbius Conjugate. Now Q1.Q2* // Q2.Q1*.