QA-Tf6 Quang Duong’s Transformation
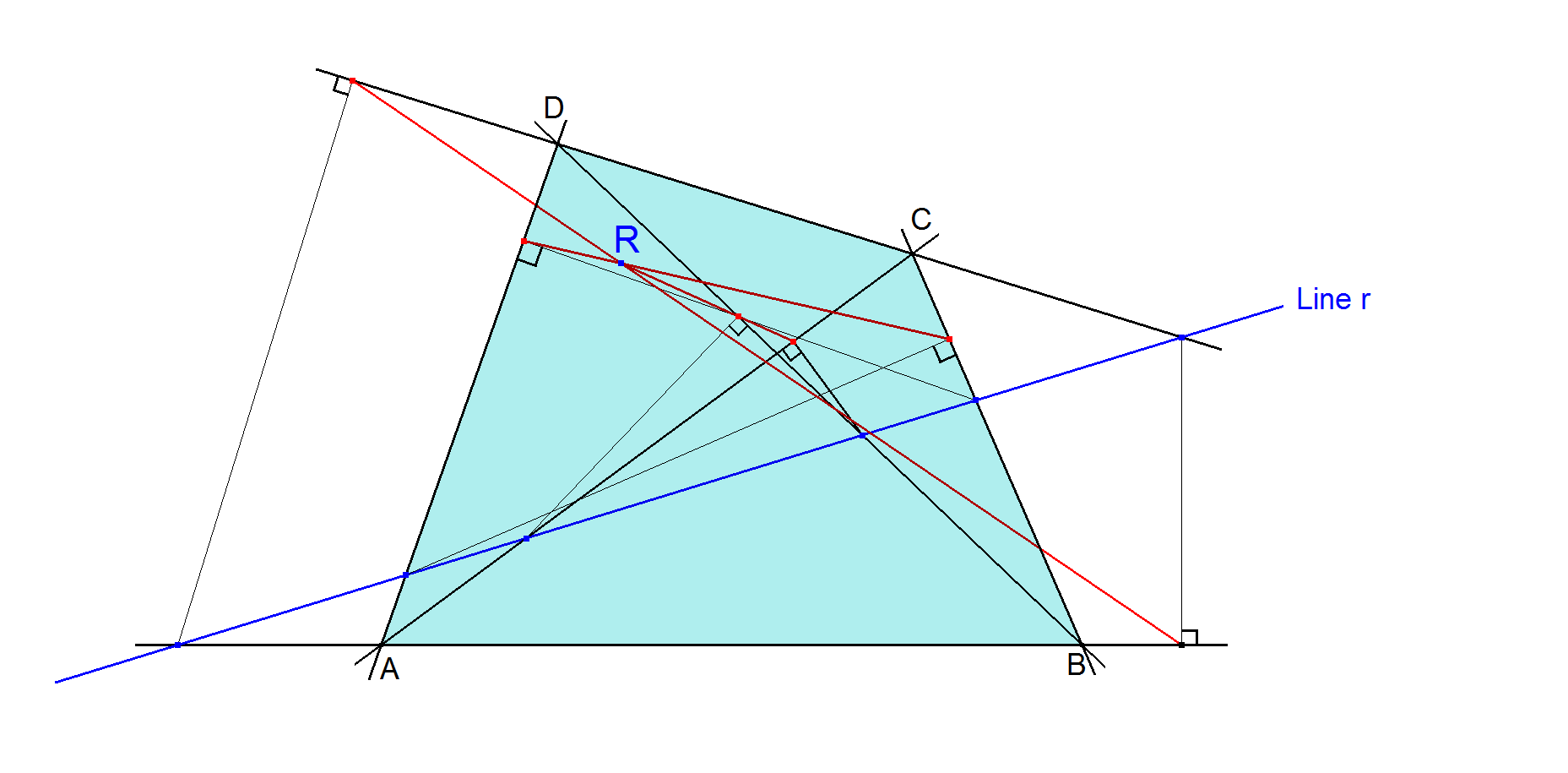
Let ABCD be the Reference Quadrangle and r a random line.
Line r intersects AB, CD, AC, DB, AD, BC at MAB, MCD, MAC, MDB, MAD, MBC.
HAB, HCD, HAC, HDB, HAD, HBC is orthogonal projections of MCD, MAB, MDB, MAC, MBC, MAD on AB, CD, AC, DB, AD, BC.
Then HAB HCD, HAC HDB, HAD HBC are concurrent in a point R being the Quang Duong’s Transformation of line r wrt Reference Quadrangle ABCD.
When vertices A,B,C,D are concyclic, then the lines HAB HCD, HAC HDB, HAD HBC will be parallel and consequently R will be an infinity point.
Alternative constructions (see Ref-34, Benedetto Scimemi, QFG # 1185):
Tables:
Following tables list the relations between several Quadrangle Objects.
General Behavior of the transformation. See Ref-34, ES#1187,1191.
|
Item
|
Transformed Item
|
|
Pencil of parallel lines
|
Line through QA-P2
|
|
Pencil of lines perpendicular to some line L1
|
L2=Line
|
|
Pencil of lines perpendicular to line L2
|
Line through QA-P2 parallel to L1
|
|
Line pencil through some point P
|
Ci=Circle through QA-P2
|
|
Line pencil through QA-Tf6(P) perpendicular to r
|
Envelope=Deltoid circumscribing Ci
|
|
Line pencil through QA-Tf6(P) parallel to r
|
Envelope=Deltoid circumscribing Ci, homothetic with the deltoid for the Simson lies of the Diagonal Triangle (wrt QA-P12 and factor 2)
|
Transformation of classes of QA-objects. See Ref-34, ES#1178,1191
|
Item
|
Transformed Item
|
|
Line through QA-P4
|
|
|
Line pencil through QA-P1
|
|
|
Line pencil through QA-P2
|
|
|
Line pencil through QA-P12
|
Circumcircle of Diagonal triangle (QA-Ci1)
|
|
Pencil of lines perpendicular to QA-L4
|
|
|
Pencil of lines perpendicular to QA-L1
|
|
|
Pencil of lines perpendicular to QA-L2
|
|
|
Tangents to circles (Ci1) round QA-P4
|
Circles (Ci2) round QA-P2
|
|
Intersection of circles Ci1 and Ci2
|
Circle through QA-P3
|
|
Radical Axes of Ci1 and Ci2
|
|
|
Tangents to Parabolas with focus QA-P4
|
|
|
Tangents to a Conic with focus QA-P4
|
Circle centered in the QA-Tf6-image of the secondary axis of the conic
|
Transformation of specific QA-Objects. See Ref-34, #1181(CvT), #1191(ES).
|
Item
|
Transformed Item
|
|
QA-L5 (Eulerline of Diagonal Triangle)
|
Point on circumcircle Diagonal Triangle
|
1st CT-coordinate for line (x:y:z):
- a2 (a2 p q - b2 p q + c2 p q + a2 p r + b2 p r - c2 p r + 2 a2 q r) x2
- b2 (a2 - b2 + c2) p q y2
- c2 (a2 + b2 - c2) p r z2
- (a2 c2 q + b2 c2 q - c4 q + a2 b2 r - b4 r + b2 c2 r) p y z
+ (a4 p q - b4 p q + 2 b2 c2 p q - c4 p q + 2 a2 b2 p r + a4 q r + a2 b2 q r - a2 c2 q r) x y
+ (2 a2 c2 p q + a4 p r - b4 p r + 2 b2 c2 p r - c4 p r + a4 q r - a2 b2 q r + a2 c2 q r) x z
Properties:
- QA-Tf6(d) is a point on the QA-Orthopolar Line QA-Tf8(d). See Ref-34, QFG#1186). For definition Orthopolar Line see Ref-13.
- Reflect some random point P in two opposite sides of the quadrangle and let M12,34 be their midpoint of these reflections. Define similarly M13,24 and M14,23. Then QA-Tf3(P) is the circumcenter of the triangle M12,34M13,24M14,23 and its circumcircle coincides with the circle described in the initial construction of QA-Tf3. QA-Tf6(Lp) will be a point on this circle for any line Lp through P. See Ref-34, Ngo Quang Duong, message #2745.