QA-Tr3: Morley Triangle
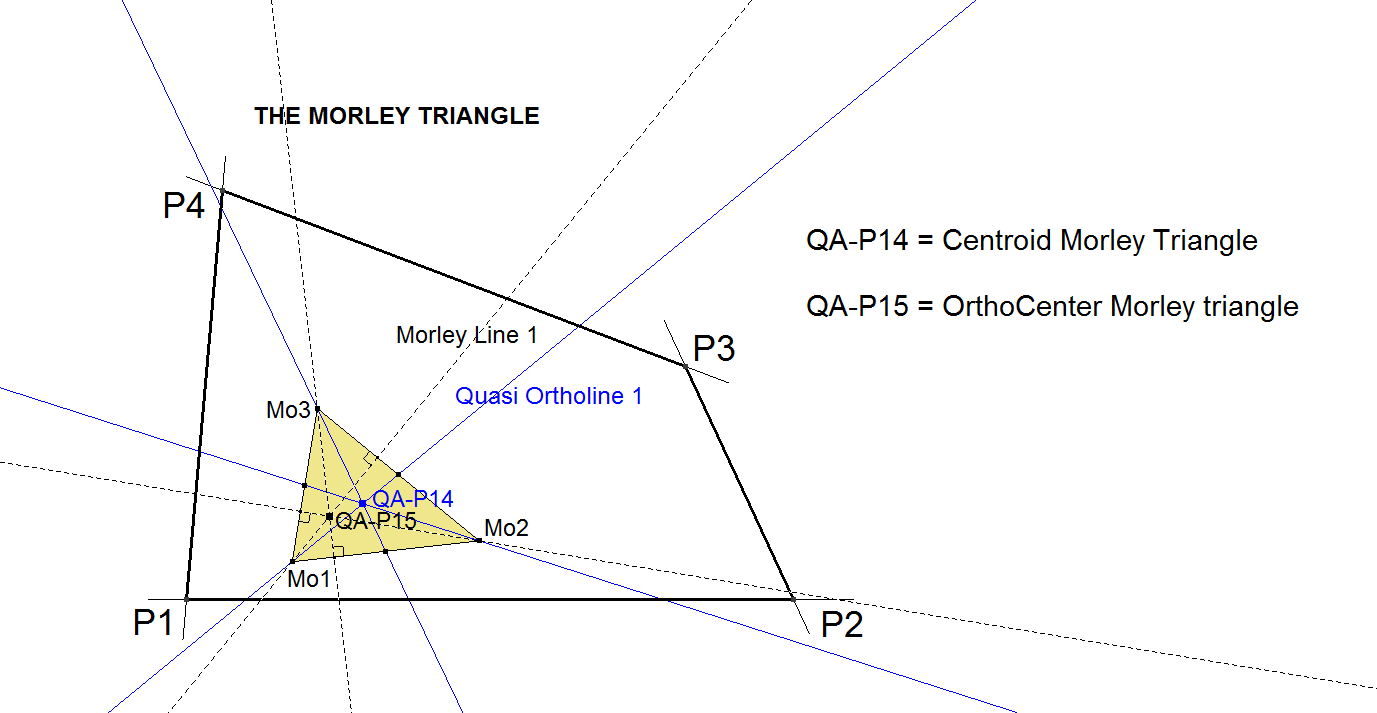
The QL-Morley Points (QL-P2) of the 3 Quadrigons of the Reference Quadrangle form a triangle Mo1.Mo2.Mo3.
The QL-Quasi Ortholines (see paragraph QL-L6: Quasi Ortholine) of the 3 Quadrigons of the Reference Quadrangle pass through Mo1, Mo2, Mo3 and are the medians of the Morley Triangle.
Their intersection point is the QA-Point QA-P14.
This point is the Centroid of the Morley Triangle.
The QL-Morley Lines (QL-L4) of the 3 Quadrigons of the Reference Quadrangle pass through Mo1, Mo2, Mo3 and are the altitudes of the Morley Triangle.
Their intersection point is the QA-Point QA-P15.
This point is the OrthoCenter of the Morley Triangle.
Areas:
Area Morley Triangle in CT-notation:
(c2pq+b2pr+a2qr)2 / (64 (p+q) (p+r) (q+r) (p+q+r) S)
Area Morley Triangle in DT-notation:
-(SA u2+SB v2+SC w2)2 / (8 S (-u+v+w) (u+v-w) (u-v+w) (u+v+w))
Properties:
- The QG-P5-Triple Triangle is homothetic with QA-Tr3 with perspector QA-P24. Its side lengths are twice the side lengths of QA-Tr3.
- The QL-P3-Triple Triangle is perspective with QA-Tr3 with perspector QA-P15.
- The QL-P10-Triple Triangle is perspective with QA-Tr3 with perspector QA-P14.
- Area QL-P2-Triple Triangle (QA-Tr3) = 4 * Area QL-P22-Triple Triangle.
- The Centroid (QA-P14) of QA-Tr3 plays a role in the construction of complements and anti-complements wrt QA-Tr3:
-
The vertices of QA-Tr3 coincide when the Reference Quadrangle is concyclic.