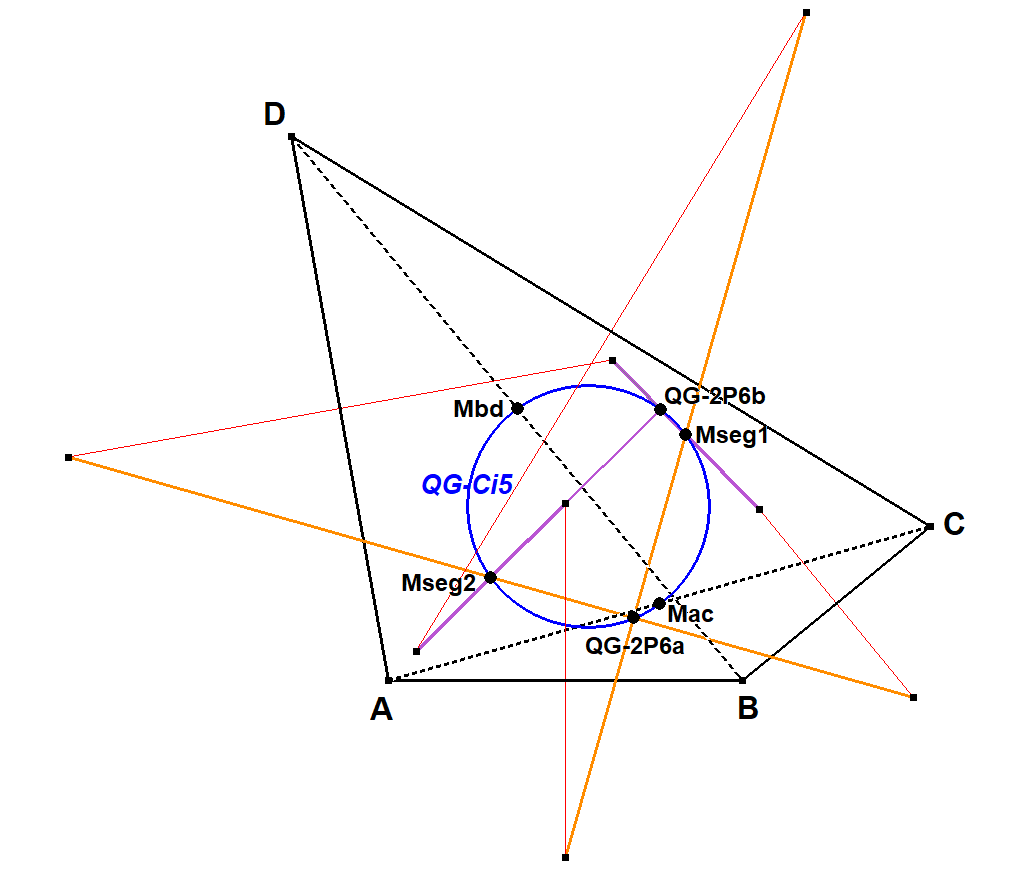
QG-Ci5: QG-Six-point Circle
The QG-Six-point circle is a circle through 6 main points especially related to the Van Aubel configuration. These six points are:
- The midpoints of the two QG-diagonals Mac and Mbd
- The Inner and Outer Van Aubel Points QG-2P6a and QG-2P6b, which also are the centers of the only possible circumscribed squares about a Quadrigon.
- The common midpoints of the Inner and Outer Van Aubel Segments Mseg1 and Mseg2.
The six-point circle is actually the circle with the midpoints of the two QG-diagonals as diameter.
Independently, Dario Pellegrinetti proved the concyclic property of the forementioned six points [68] and Eckart Schmidt showed that the Thales circle of the midpoints of the QG-diagonals passes through the Van Aubel points (personal note).
CT-Equation QG-Ci5 in 1st QA-Quadrigon:
(a2 p – b2 p – c2 p + 2 a2 q – 2 b2 q – 2 c2 q + a2 r – 3 b2 r – c2 r) x2
+ (-a2 p + b2 p – 3 c2 p – 3 a2 r + b2 r – c2 r) y2
+ (-a2 p – 3 b2 p + c2 p – 2 a2 q – 2 b2 q + 2 c2 q – a2 r – b2 r + c2 r) z2
+ 2 (2 c2 p + a2 q – b2 q + 3 c2 q – a2 r – b2 r + 3 c2 r) x y
+ 2 (3 a2 p – b2 p – c2 p + 3 a2 q – b2 q + c2 q + 2 a2 r) y z
+ 4 b2 (p + q + r) x z
Properties
- The center of QG-Ci5 is the Quadrangle Centroid QA-P1.
- The circle is the locus of centers of all circumscribed rectangles about a Quadrigon.
- QG-Ci5 is the circle with diameter Mac.Mbd as well as the circle with diameter Mseg1.Mseg2.
Estimated human page views: 1175
