QG-Co1: Inscribed Harmonic Conic
There is a projective transformation from 4 lines in a square to any other set of 4 lines.
See chapter QG-Tf1: QG-Projective Square Transformation.
The Inscribed Harmonic Conic is the projective transformation of the inscribed circle in a square to the Reference Quadrigon. This conic touches the sidelines of the Quadrigon in their perspective midpoints.
See picture below.
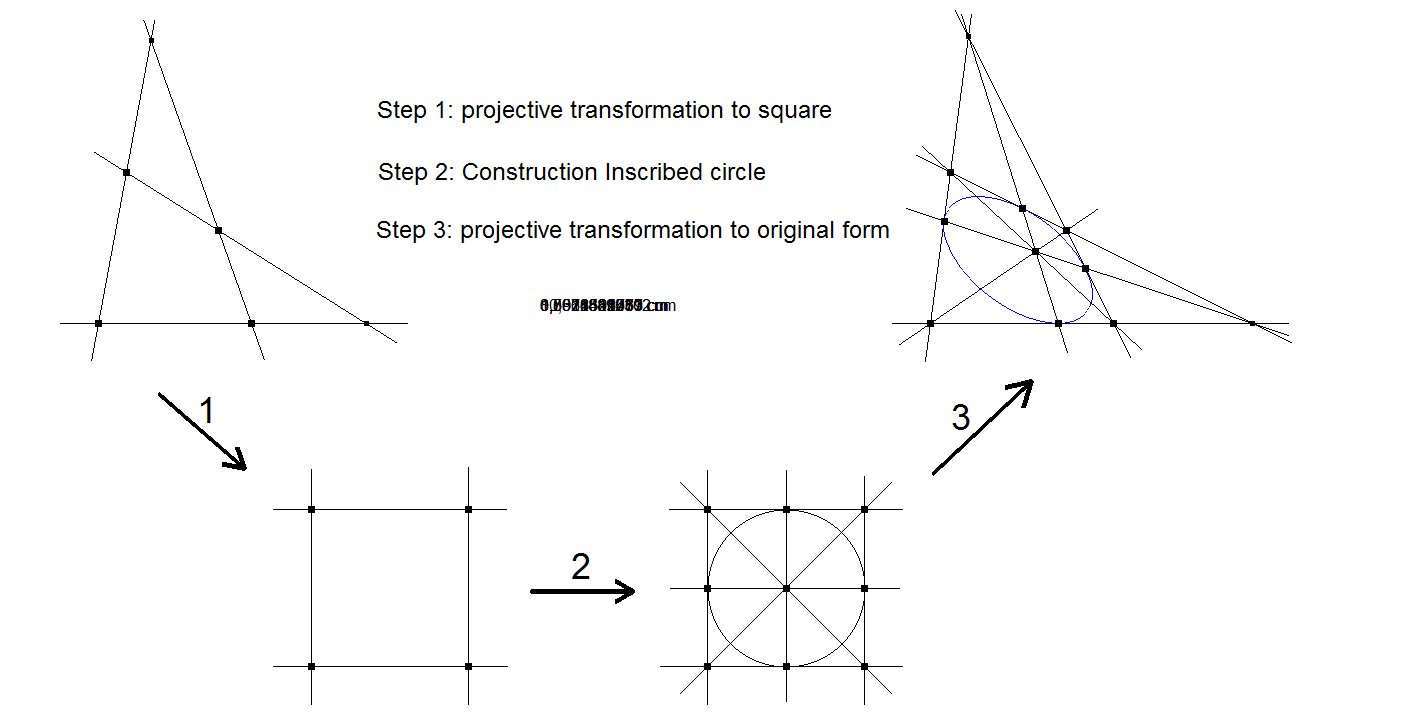
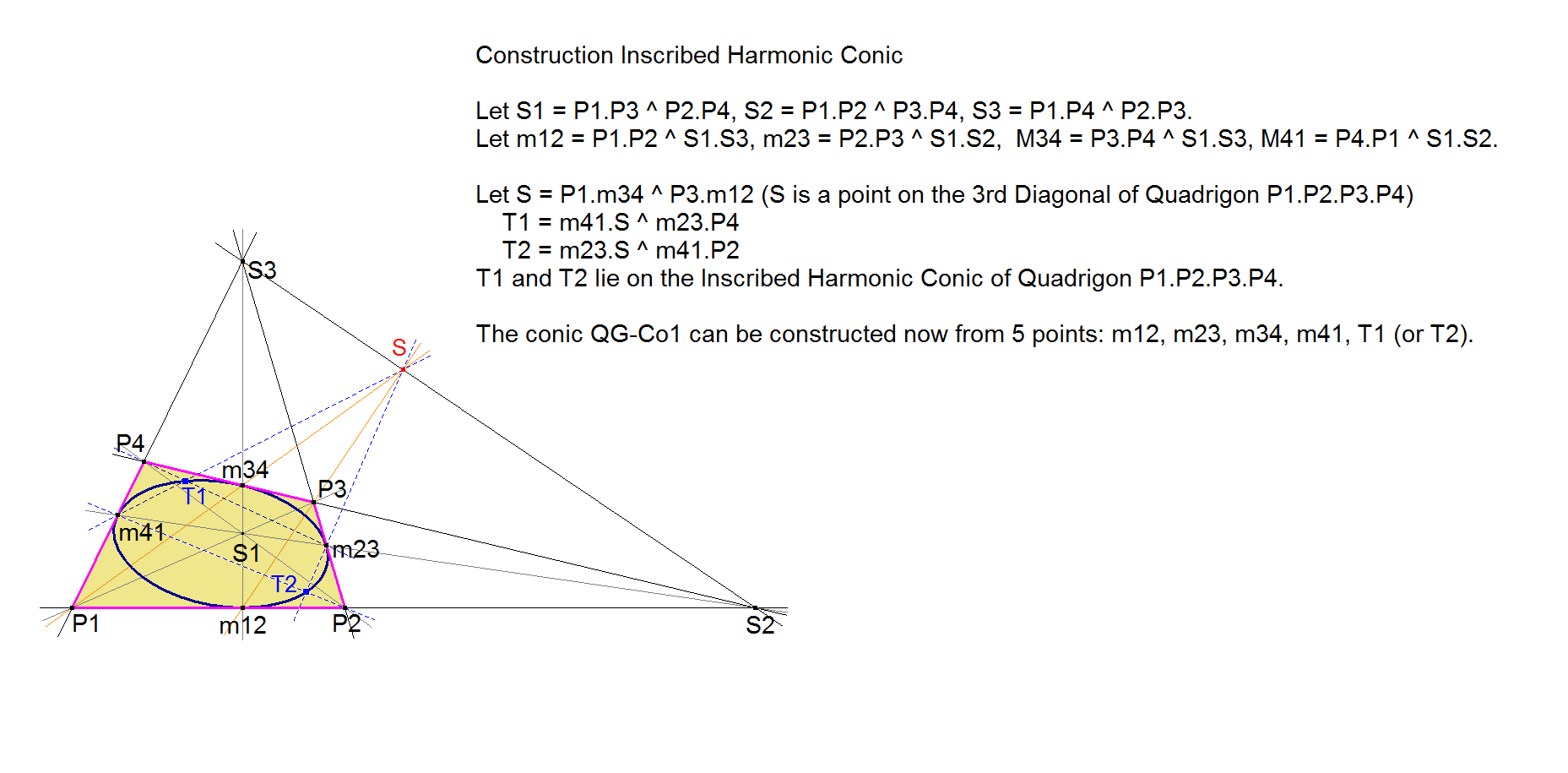
Construction QG-Co1
Equation QG-Co1 in 3 QA-Quadrigons in CT-notation:
q2 r2 x2 + p2 r2 y2 + p2 q2 z2 – 6 p q r2 x y + 2 p2 q r y z + 2 p q2 r x z
q2 r2 x2 + p2 r2 y2 + p2 q2 z2 + 2 p q r2 x y – 6 p2 q r y z + 2 p q2 r x z
q2 r2 x2 + p2 r2 y2 + p2 q2 z2 + 2 p q r2 x y + 2 p2 q r y z – 6 p q2 r x z
Equation QG-Co1 in 3 QL-Quadrigons in CT-notation:
l2 x2 + m2 y2 + 4 n2 z2 – 2 l m x y + 4 m n y z + 4 l n x z
4 l2 x2 + m2 y2 + n2 z2 + 4 l m x y – 2 m n y z + 4 l n x z
l2 x2 + 4 m2 y2 + n2 z2 + 4 l m x y + 4 m n y z – 2 l n x z
Equation QG-Co1 in 3 QA-Quadrigons in DT-notation:
q2 r2 x2 – p2 r2 y2 + p2 q2 z2
-r2 q2 x2 + r2 p2 y2 + p2 q2 z2
q2 r2 x2 + r2 p2 y2 – q2 p2 z2
Equation QG-Co1 in 3 QL-Quadrigons in DT-notation:
2 x2 l2 – y2 m2 + 2 z2 n2
-x2 l2 + 2 y2 m2 + 2 z2 n2
2 x2 l2 + 2 y2 m2 – z2 n2
Properties
- The Center of QG-Co1 is QG-P12.
- The Diagonal Triangles QA-Tr1 and QL-Tr1 are self-polar wrt QG-Co1.
- The Triangle QG-P1.QG-P2.QG-P3 is self-polar wrt QG-Co1.
Estimated human page views: 513
