QG-Cu1: Van Aubel Cubic
Erect Perpendicular Bisectors on the sides of quadrilateral P1.P2.P3.P4.
Make them as long as a fixed ratio of the side they are on.
Connect opposite points. This give 2 new lines.
The locus of their intersection points is QG-Cu1.
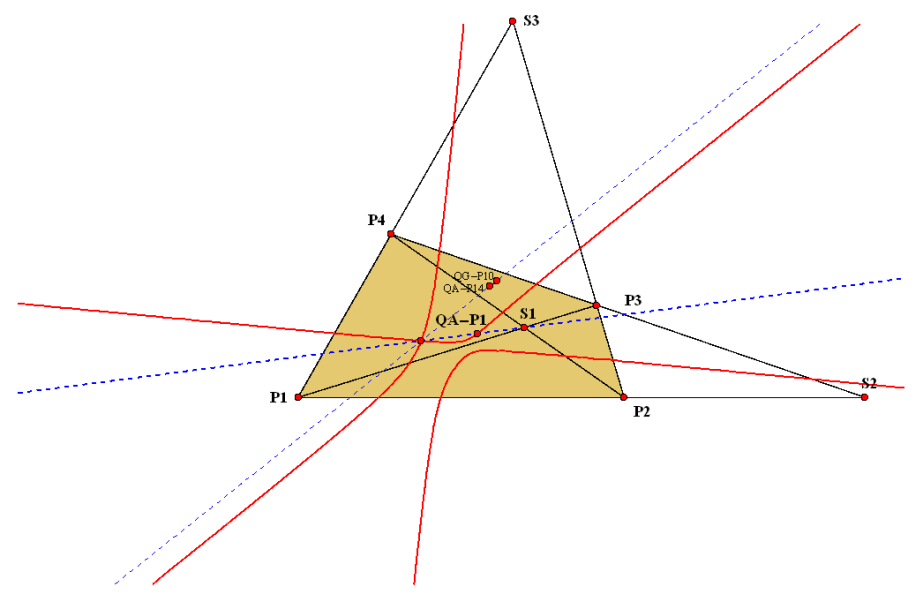
When the fixed ratio is + ½ we have the famous Van Aubel Constellation. With this ration the 2 connecting line segments are perpendicular and equal in length. See [8], Aubel, Stelling van Van, and [13] Van Aubel’s Theorem.
Equation QG-Cu1 in CT-Coordinates
(a4 p2 q2 – 2 a2 b2 p2 q2 + b4 p2 q2 – 2 a2 c2 p2 q2 + 2 b2 c2 p2 q2 + c4 p2 q2 + 2 a4 p q3 – 4 a2 b2 p q3 + 2 b4 p q3 – 4 a2 c2 p q3 + 4 b2 c2 p q3 + 2 c4 p q3 + a4 q4 – 2 a2 b2 q4 + b4 q4 – 2 a2 c2 q4 + 2 b2 c2 q4 + c4 q4 – 2 a2 b2 p2 q r + 2 b4 p2 q r + 2 b2 c2 p2 q r + 2 a4 p q2 r – 8 a2 b2 p q2 r + 6 b4 p q2 r – 4 a2 c2 p q2 r + 8 b2 c2 p q2 r + 2 c4 p q2 r + 2 a4 q3 r – 6 a2 b2 q3 r + 4 b4 q3 r – 4 a2 c2 q3 r + 6 b2 c2 q3 r + 2 c4 q3 r + b4 p2 r2 – b2 c2 p2 r2 + a4 p q r2 – 6 a2 b2 p q r2 + 7 b4 p q r2 – 2 a2 c2 p q r2 + 2 b2 c2 p q r2 + c4 p q r2 + 2 a4 q2 r2 – 8 a2 b2 q2 r2 + 7 b4 q2 r2 – 4 a2 c2 q2 r2 + 4 b2 c2 q2 r2 + 2 c4 q2 r2 – a2 b2 p r3 + 3 b4 p r3 – b2 c2 p r3 + a4 q r3 – 4 a2 b2 q r3 + 5 b4 q r3 – 2 a2 c2 q r3 + c4 q r3 – a2 b2 r4 + b4 r4) x3
+ (-2 a4 p3 q + 4 a2 b2 p3 q – 2 b4 p3 q + 2 a2 c2 p3 q – 2 b2 c2 p3 q – 5 a4 p2 q2 + 10 a2 b2 p2 q2 – 5 b4 p2 q2 + 8 a2 c2 p2 q2 – 8 b2 c2 p2 q2 – 3 c4 p2 q2 – 4 a4 p q3 + 8 a2 b2 p q3 – 4 b4 p q3 + 8 a2 c2 p q3 – 8 b2 c2 p q3 – 4 c4 p q3 – a4 q4 + 2 a2 b2 q4 – b4 q4 + 2 a2 c2 q4 – 2 b2 c2 q4 – c4 q4 + 2 a2 b2 p3 r – 2 b4 p3 r – 2 b2 c2 p3 r – 6 a4 p2 q r + 16 a2 b2 p2 q r – 10 b4 p2 q r + 6 a2 c2 p2 q r – 14 b2 c2 p2 q r – 10 a4 p q2 r + 22 a2 b2 p q2 r – 12 b4 p q2 r + 16 a2 c2 p q2 r – 22 b2 c2 p q2 r – 6 c4 p q2 r – 4 a4 q3 r + 8 a2 b2 q3 r – 4 b4 q3 r + 8 a2 c2 q3 r – 8 b2 c2 q3 r – 4 c4 q3 r – a4 p2 r2 + 8 a2 b2 p2 r2 – 6 b4 p2 r2 – 3 b2 c2 p2 r2 + c4 p2 r2 – 8 a4 p q r2 + 24 a2 b2 p q r2 – 14 b4 p q r2 + 10 a2 c2 p q r2 – 18 b2 c2 p q r2 – 2 c4 p q r2 – 6 a4 q2 r2 + 14 a2 b2 q2 r2 – 7 b4 q2 r2 + 10 a2 c2 q2 r2 – 12 b2 c2 q2 r2 – 4 c4 q2 r2 – 3 a4 p r3 + 11 a2 b2 p r3 – 6 b4 p r3 + 2 a2 c2 p r3 – 5 b2 c2 p r3 + c4 p r3 – 4 a4 q r3 + 12 a2 b2 q r3 – 6 b4 q r3 + 6 a2 c2 q r3 – 6 b2 c2 q r3 – 2 c4 q r3 – 2 a4 r4 + 3 a2 b2 r4 – b4 r4 + 2 a2 c2 r4 – 2 b2 c2 r4) x2 y
+ (a4 p4 – 2 a2 b2 p4 + b4 p4 – b2 c2 p4 + 3 a4 p3 q – 6 a2 b2 p3 q + 3 b4 p3 q – 4 a2 c2 p3 q + 2 b2 c2 p3 q + c4 p3 q + 3 a4 p2 q2 – 6 a2 b2 p2 q2 + 3 b4 p2 q2 – 6 a2 c2 p2 q2 + 5 b2 c2 p2 q2 + 3 c4 p2 q2 + a4 p q3 – 2 a2 b2 p q3 + b4 p q3 – 2 a2 c2 p q3 + 2 b2 c2 p q3 + c4 p q3 + 4 a4 p3 r – 7 a2 b2 p3 r + 3 b4 p3 r – 2 a2 c2 p3 r + b2 c2 p3 r + 2 c4 p3 r + 9 a4 p2 q r – 14 a2 b2 p2 q r + 5 b4 p2 q r – 14 a2 c2 p2 q r + 8 b2 c2 p2 q r + 5 c4 p2 q r + 6 a4 p q2 r – 7 a2 b2 p q2 r + b4 p q2 r – 12 a2 c2 p q2 r + 5 b2 c2 p q2 r + 6 c4 p q2 r + a4 q3 r – b4 q3 r – 2 a2 c2 q3 r + c4 q3 r + 5 a4 p2 r2 – 7 a2 b2 p2 r2 + b4 p2 r2 – 4 a2 c2 p2 r2 + 5 b2 c2 p2 r2 + c4 p2 r2 + 7 a4 p q r2 – 6 a2 b2 p q r2 – 3 b4 p q r2 – 12 a2 c2 p q r2 + 10 b2 c2 p q r2 + 5 c4 p q r2 + 2 a4 q2 r2 + a2 b2 q2 r2 – 4 b4 q2 r2 – 4 a2 c2 q2 r2 + 2 b2 c2 q2 r2 + 2 c4 q2 r2 + 2 a4 p r3 – a2 b2 p r3 – 3 b4 p r3 – 6 a2 c2 p r3 + 7 b2 c2 p r3 + a4 q r3 + 2 a2 b2 q r3 – 5 b4 q r3 – 2 a2 c2 q r3 + 4 b2 c2 q r3 + c4 q r3 – a4 r4 + 3 a2 b2 r4 – 2 b4 r4 – 2 a2 c2 r4 + 2 b2 c2 r4) x y2
+ (-b2 c2 p4 + c4 p4 – 2 b2 c2 p3 q – b2 c2 p2 q2 – a4 p3 r + a2 b2 p3 r + 2 a2 c2 p3 r – b2 c2 p3 r – c4 p3 r – 2 a4 p2 q r + 2 a2 b2 p2 q r + 4 a2 c2 p2 q r – 2 c4 p2 q r – a4 p q2 r + a2 b2 p q2 r + 2 a2 c2 p q2 r + b2 c2 p q2 r – c4 p q2 r – 2 a4 p2 r2 + a2 b2 p2 r2 + 2 a2 c2 p2 r2 + b2 c2 p2 r2 – 2 c4 p2 r2 – 2 a4 p q r2 + 4 a2 c2 p q r2 + 2 b2 c2 p q r2 – 2 c4 p q r2 – a2 b2 q2 r2 – a4 p r3 – a2 b2 p r3 + 2 a2 c2 p r3 + b2 c2 p r3 – c4 p r3 – 2 a2 b2 q r3 + a4 r4 – a2 b2 r4) y3 + (2 a4 p3 q – 2 a2 b2 p3 q – 4 a2 c2 p3 q + 2 b2 c2 p3 q + 2 c4 p3 q + 5 a4 p2 q2 – 2 a2 b2 p2 q2 – 3 b4 p2 q2 – 10 a2 c2 p2 q2 + 2 b2 c2 p2 q2 + 5 c4 p2 q2 + 6 a4 p q3 – 2 a2 b2 p q3 – 4 b4 p q3 – 12 a2 c2 p q3 + 2 b2 c2 p q3 + 6 c4 p q3 + 3 a4 q4 – 2 a2 b2 q4 – b4 q4 – 6 a2 c2 q4 + 2 b2 c2 q4 + 3 c4 q4 – 2 a2 b2 p3 r + 4 b2 c2 p3 r + 4 a4 p2 q r – 6 a2 b2 p2 q r – 6 b4 p2 q r – 8 a2 c2 p2 q r + 14 b2 c2 p2 q r + 4 c4 p2 q r + 8 a4 p q2 r – 8 a2 b2 p q2 r – 10 b4 p q2 r – 16 a2 c2 p q2 r + 16 b2 c2 p q2 r + 8 c4 p q2 r + 6 a4 q3 r – 8 a2 b2 q3 r – 2 b4 q3 r – 12 a2 c2 q3 r + 8 b2 c2 q3 r + 6 c4 q3 r + a4 p2 r2 – 6 a2 b2 p2 r2 – 2 b4 p2 r2 – 2 a2 c2 p2 r2 + 9 b2 c2 p2 r2 + c4 p2 r2 + 5 a4 p q r2 – 12 a2 b2 p q r2 – 7 b4 p q r2 – 10 a2 c2 p q r2 + 16 b2 c2 p q r2 + 5 c4 p q r2 + 6 a4 q2 r2 – 12 a2 b2 q2 r2 – b4 q2 r2 – 12 a2 c2 q2 r2 + 8 b2 c2 q2 r2 + 6 c4 q2 r2 + 2 a4 p r3 – 5 a2 b2 p r3 – 3 b4 p r3 – 4 a2 c2 p r3 + 5 b2 c2 p r3 + 2 c4 p r3 + 3 a4 q r3 – 8 a2 b2 q r3 – b4 q r3 – 6 a2 c2 q r3 + 4 b2 c2 q r3 + 3 c4 q r3 + a4 r4 – a2 b2 r4 – 2 a2 c2 r4 + c4 r4) x2 z
+ 2 (-a4 p4 + a2 b2 p4 + a2 c2 p4 – 3 a4 p3 q + 3 b4 p3 q + 6 a2 c2 p3 q – 3 c4 p3 q – 5 a4 p2 q2 – a2 b2 p2 q2 + 6 b4 p2 q2 + 10 a2 c2 p2 q2 + b2 c2 p2 q2 – 5 c4 p2 q2 – 4 a4 p q3 + 4 b4 p q3 + 8 a2 c2 p q3 – 4 c4 p q3 – a4 q4 + b4 q4 + 2 a2 c2 q4 – c4 q4 – 3 a4 p3 r + 4 b4 p3 r + 4 a2 c2 p3 r – 3 b2 c2 p3 r – c4 p3 r – 7 a4 p2 q r – 4 a2 b2 p2 q r + 13 b4 p2 q r + 14 a2 c2 p2 q r – 4 b2 c2 p2 q r – 7 c4 p2 q r – 9 a4 p q2 r – 2 a2 b2 p q2 r + 12 b4 p q2 r + 18 a2 c2 p q2 r – 2 b2 c2 p q2 r – 9 c4 p q2 r – 4 a4 q3 r + 4 b4 q3 r + 8 a2 c2 q3 r – 4 c4 q3 r – 3 a4 p2 r2 – 4 a2 b2 p2 r2 + 7 b4 p2 r2 + 6 a2 c2 p2 r2 – 4 b2 c2 p2 r2 – 3 c4 p2 r2 – 7 a4 p q r2 – 4 a2 b2 p q r2 + 13 b4 p q r2 + 14 a2 c2 p q r2 – 4 b2 c2 p q r2 – 7 c4 p q r2 – 5 a4 q2 r2 + a2 b2 q2 r2 + 6 b4 q2 r2 + 10 a2 c2 q2 r2 – b2 c2 q2 r2 – 5 c4 q2 r2 – a4 p r3 – 3 a2 b2 p r3 + 4 b4 p r3 + 4 a2 c2 p r3 – 3 c4 p r3 – 3 a4 q r3 + 3 b4 q r3 + 6 a2 c2 q r3 – 3 c4 q r3 + a2 c2 r4 + b2 c2 r4 – c4 r4) x y z + (2 a2 b2 p4 – 2 b4 p4 – 2 a2 c2 p4 + 3 b2 c2 p4 – c4 p4 + a4 p3 q + 4 a2 b2 p3 q – 5 b4 p3 q – 2 a2 c2 p3 q + 2 b2 c2 p3 q + c4 p3 q + 2 a4 p2 q2 + 2 a2 b2 p2 q2 – 4 b4 p2 q2 – 4 a2 c2 p2 q2 + b2 c2 p2 q2 + 2 c4 p2 q2 + a4 p q3 – b4 p q3 – 2 a2 c2 p q3 + c4 p q3 + 7 a2 b2 p3 r – 3 b4 p3 r – 6 a2 c2 p3 r – b2 c2 p3 r + 2 c4 p3 r + 5 a4 p2 q r + 10 a2 b2 p2 q r – 3 b4 p2 q r – 12 a2 c2 p2 q r – 6 b2 c2 p2 q r + 7 c4 p2 q r + 6 a4 p q2 r + 5 a2 b2 p q2 r + b4 p q2 r – 12 a2 c2 p q2 r – 7 b2 c2 p q2 r + 6 c4 p q2 r + a4 q3 r + 2 a2 b2 q3 r + b4 q3 r – 2 a2 c2 q3 r – 2 b2 c2 q3 r + c4 q3 r + a4 p2 r2 + 5 a2 b2 p2 r2 + b4 p2 r2 – 4 a2 c2 p2 r2 – 7 b2 c2 p2 r2 + 5 c4 p2 r2 + 5 a4 p q r2 + 8 a2 b2 p q r2 + 5 b4 p q r2 – 14 a2 c2 p q r2 – 14 b2 c2 p q r2 + 9 c4 p q r2 + 3 a4 q2 r2 + 5 a2 b2 q2 r2 + 3 b4 q2 r2 – 6 a2 c2 q2 r2 – 6 b2 c2 q2 r2 + 3 c4 q2 r2 + 2 a4 p r3 + a2 b2 p r3 + 3 b4 p r3 – 2 a2 c2 p r3 – 7 b2 c2 p r3 + 4 c4 p r3 + a4 q r3 + 2 a2 b2 q r3 + 3 b4 q r3 – 4 a2 c2 q r3 – 6 b2 c2 q r3 + 3 c4 q r3 – a2 b2 r4 + b4 r4 – 2 b2 c2 r4 + c4 r4) y2 z
+ (a4 p4 – 2 a2 c2 p4 – b2 c2 p4 + c4 p4 + 3 a4 p3 q + 4 a2 b2 p3 q – b4 p3 q – 6 a2 c2 p3 q – 8 b2 c2 p3 q + 3 c4 p3 q + 6 a4 p2 q2 + 8 a2 b2 p2 q2 – b4 p2 q2 – 12 a2 c2 p2 q2 – 12 b2 c2 p2 q2 + 6 c4 p2 q2 + 6 a4 p q3 + 8 a2 b2 p q3 – 2 b4 p q3 – 12 a2 c2 p q3 – 8 b2 c2 p q3 + 6 c4 p q3 + 3 a4 q4 + 2 a2 b2 q4 – b4 q4 – 6 a2 c2 q4 – 2 b2 c2 q4 + 3 c4 q4 + 2 a4 p3 r + 5 a2 b2 p3 r – 3 b4 p3 r – 4 a2 c2 p3 r – 5 b2 c2 p3 r + 2 c4 p3 r + 5 a4 p2 q r + 16 a2 b2 p2 q r – 7 b4 p2 q r – 10 a2 c2 p2 q r – 12 b2 c2 p2 q r + 5 c4 p2 q r + 8 a4 p q2 r + 16 a2 b2 p q2 r – 10 b4 p q2 r – 16 a2 c2 p q2 r – 8 b2 c2 p q2 r + 8 c4 p q2 r + 6 a4 q3 r + 2 a2 b2 q3 r – 4 b4 q3 r – 12 a2 c2 q3 r – 2 b2 c2 q3 r + 6 c4 q3 r + a4 p2 r2 + 9 a2 b2 p2 r2 – 2 b4 p2 r2 – 2 a2 c2 p2 r2 – 6 b2 c2 p2 r2 + c4 p2 r2 + 4 a4 p q r2 + 14 a2 b2 p q r2 – 6 b4 p q r2 – 8 a2 c2 p q r2 – 6 b2 c2 p q r2 + 4 c4 p q r2 + 5 a4 q2 r2 + 2 a2 b2 q2 r2 – 3 b4 q2 r2 – 10 a2 c2 q2 r2 – 2 b2 c2 q2 r2 + 5 c4 q2 r2 + 4 a2 b2 p r3 – 2 b2 c2 p r3 + 2 a4 q r3 + 2 a2 b2 q r3 – 4 a2 c2 q r3 – 2 b2 c2 q r3 + 2 c4 q r3) x z2
+ (-2 a2 b2 p4 – b4 p4 + 2 a2 c2 p4 + 3 b2 c2 p4 – 2 c4 p4 – 2 a4 p3 q – 6 a2 b2 p3 q – 6 b4 p3 q + 6 a2 c2 p3 q + 12 b2 c2 p3 q – 4 c4 p3 q – 4 a4 p2 q2 – 12 a2 b2 p2 q2 – 7 b4 p2 q2 + 10 a2 c2 p2 q2 + 14 b2 c2 p2 q2 – 6 c4 p2 q2 – 4 a4 p q3 – 8 a2 b2 p q3 – 4 b4 p q3 + 8 a2 c2 p q3 + 8 b2 c2 p q3 – 4 c4 p q3 – a4 q4 – 2 a2 b2 q4 – b4 q4 + 2 a2 c2 q4 + 2 b2 c2 q4 – c4 q4 + a4 p3 r – 5 a2 b2 p3 r – 6 b4 p3 r + 2 a2 c2 p3 r + 11 b2 c2 p3 r – 3 c4 p3 r – 2 a4 p2 q r – 18 a2 b2 p2 q r – 14 b4 p2 q r + 10 a2 c2 p2 q r + 24 b2 c2 p2 q r – 8 c4 p2 q r – 6 a4 p q2 r – 22 a2 b2 p q2 r – 12 b4 p q2 r + 16 a2 c2 p q2 r + 22 b2 c2 p q2 r – 10 c4 p q2 r – 4 a4 q3 r – 8 a2 b2 q3 r – 4 b4 q3 r + 8 a2 c2 q3 r + 8 b2 c2 q3 r – 4 c4 q3 r + a4 p2 r2 – 3 a2 b2 p2 r2 – 6 b4 p2 r2 + 8 b2 c2 p2 r2 – c4 p2 r2 – 14 a2 b2 p q r2 – 10 b4 p q r2 + 6 a2 c2 p q r2 + 16 b2 c2 p q r2 – 6 c4 p q r2 – 3 a4 q2 r2 – 8 a2 b2 q2 r2 – 5 b4 q2 r2 + 8 a2 c2 q2 r2 + 10 b2 c2 q2 r2 – 5 c4 q2 r2 – 2 a2 b2 p r3 – 2 b4 p r3 + 2 b2 c2 p r3 – 2 a2 b2 q r3 – 2 b4 q r3 + 2 a2 c2 q r3 + 4 b2 c2 q r3 – 2 c4 q r3) y z2
+ (b4 p4 – b2 c2 p4 + a4 p3 q + 5 b4 p3 q – 2 a2 c2 p3 q – 4 b2 c2 p3 q + c4 p3 q + 2 a4 p2 q2 + 4 a2 b2 p2 q2 + 7 b4 p2 q2 – 4 a2 c2 p2 q2 – 8 b2 c2 p2 q2 + 2 c4 p2 q2 + 2 a4 p q3 + 6 a2 b2 p q3 + 4 b4 p q3 – 4 a2 c2 p q3 – 6 b2 c2 p q3 + 2 c4 p q3 + a4 q4 + 2 a2 b2 q4 + b4 q4 – 2 a2 c2 q4 – 2 b2 c2 q4 + c4 q4 – a2 b2 p3 r + 3 b4 p3 r – b2 c2 p3 r + a4 p2 q r + 2 a2 b2 p2 q r + 7 b4 p2 q r – 2 a2 c2 p2 q r – 6 b2 c2 p2 q r + c4 p2 q r + 2 a4 p q2 r + 8 a2 b2 p q2 r + 6 b4 p q2 r – 4 a2 c2 p q2 r – 8 b2 c2 p q2 r + 2 c4 p q2 r + 2 a4 q3 r + 4 a2 b2 q3 r + 2 b4 q3 r – 4 a2 c2 q3 r – 4 b2 c2 q3 r + 2 c4 q3 r – a2 b2 p2 r2 + b4 p2 r2 + 2 a2 b2 p q r2 + 2 b4 p q r2 – 2 b2 c2 p q r2 + a4 q2 r2 + 2 a2 b2 q2 r2 + b4 q2 r2 – 2 a2 c2 q2 r2 – 2 b2 c2 q2 r2 + c4 q2 r2) z3
Properties
- One asymptote // QG-P10.QA-P14.QL-P2.QL-P10 (which actually is QL-L6 in the Quadrigon).
- The other 2 asymptotes are mutually perpendicular.
- The self-intersecting point of the cubic is QG-P1.QA-P1 ^ QG-P10.QA-P14.
- Its Involutary Conjugate is a point on the line QG-P1. QA-P20.
- Let (QG) be the Quadrigon formed by the endpoints of the erected perpendicular bisectors. Lines of this Quadrigon are noted between brackets.
- (QL-L1) = QG-P7.QG-P9 and (QG-P7.QG-P9) = QL-L1. (Eckart Schmidt, September 15, 2013). These lines are mutually perpendicular.
Estimated human page views: 685
