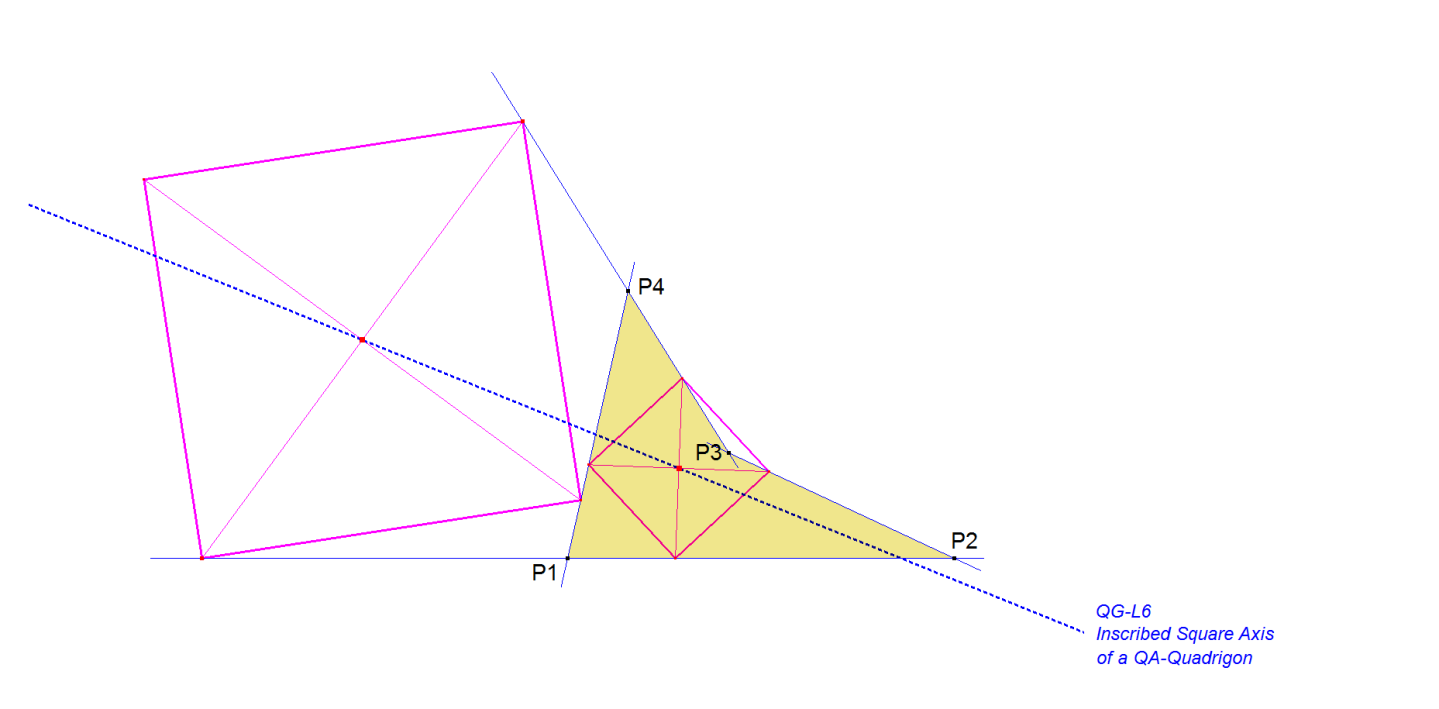
QG-L6: Inscribed Square Axis
QG-L6 is the line connecting the centers of the 2 possible Inscribed Squares in a Quadrigon.
This line is also mentioned at QA-P23.
CT-Coefficients QG-L6 in 1st QA-Quadrigon
(2 SB q3 r – 2 SC p q r2 + c2 p q2 (p + 2 q + 2 r) – (b2 – c2) q2 r2 – b2 p2 r2 :
2 SC p q r2 + a2 q2 r2 + p2 (-c2 q2 – 2 SA q r + (a2 – c2) r2) :
2 SA p2 q r – 2 SB p q3 – a2 q2 r (2 p + 2 q + r) – (a2 – b2) p2 q2 + b2 p2 r2)
CT-Coefficients QG-L6 in 1st QL-Quadrigon
(-2 SA l m n2 – 2 SB l2 n2 + 2 SC l3 m – (b2 – c2) l3 n + c2 l n3 :
-4 SA m2 n2 + 4 SC l2 m2 + a2 l3 (-2 m + n) – c2 n3 (-2 m + l) – 2 (a2 – b2) l m n2 – 2 (b2 – c2) l2 m n :
-2 SA m n3 + 2 SC l2 m n + 2 SB l2 n2 – a2 l3 n – (a2 – b2) l n3 )
DT-Coefficients QG-L6 in 1st QA-Quadrigon
(1 : (-p2 SA + r2 SC) / (q2 SB) : -1)
DT-Coefficients QG-L6 in 1st QL-Quadrigon
(l2 : 2 l m2 n (n4 SA + l4 SC – l n b2 (l2 – l n – n2)) / ((l2 + n2) ( -l2 + 2 l n + n2)(n2 SA + l2 SC) – (l2 – n2)3 SB) : n2)
Properties
-
- QG-P2 and QA-P23 lie on QG-L6.
- QG-P2 and QA-P23 lie with the centers of the inscribed squares in harmonic position (Eckart Schmidt, September 6, 2012).
- The centers of the Inscribed Squares lie center symmetric on a conic which is the QA-Tf2-mapping of the circle with diameter the vertices on the baseline of the QA-Diagonal Triangle. The tangents at the centers of the Inscribed Squares to this conic are parallel to QG-L1 (Eckart Schmidt, September 6, 2012).
- QG-L6 is the Trilinear Polar of a point TL on QG-L2 wrt the QL-Diagonal Triangle QL-Tr1 (the trilinear polar of P is the perspectrix of the Cevian triangle of P and the Reference Triangle, see [13]) (Eckart Schmidt, September 6, 2012).
- QG-L6 is the Trilinear Polar of a point TA on QG-P1.QG-P14 (line parallel to QG-L1) wrt the QA-Diagonal Triangle (QA-Tr1) (Eckart Schmidt, September 6, 2012).
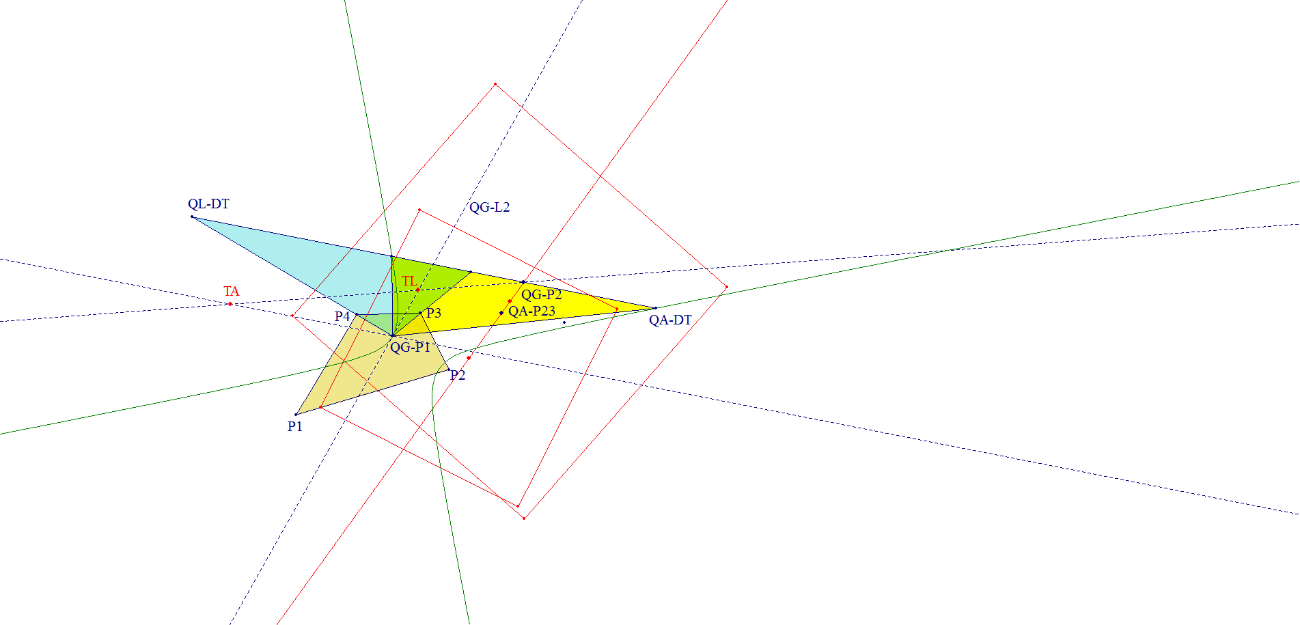
- The Trilinear Poles TA und TL of QG-L6 wrt QA-DT und QL-DT are collinear with QG-P2 (Eckart Schmidt, September 6, 2012).
Estimated human page views: 519
