QG-2P3: Endpoints 3rd QL-diagonal
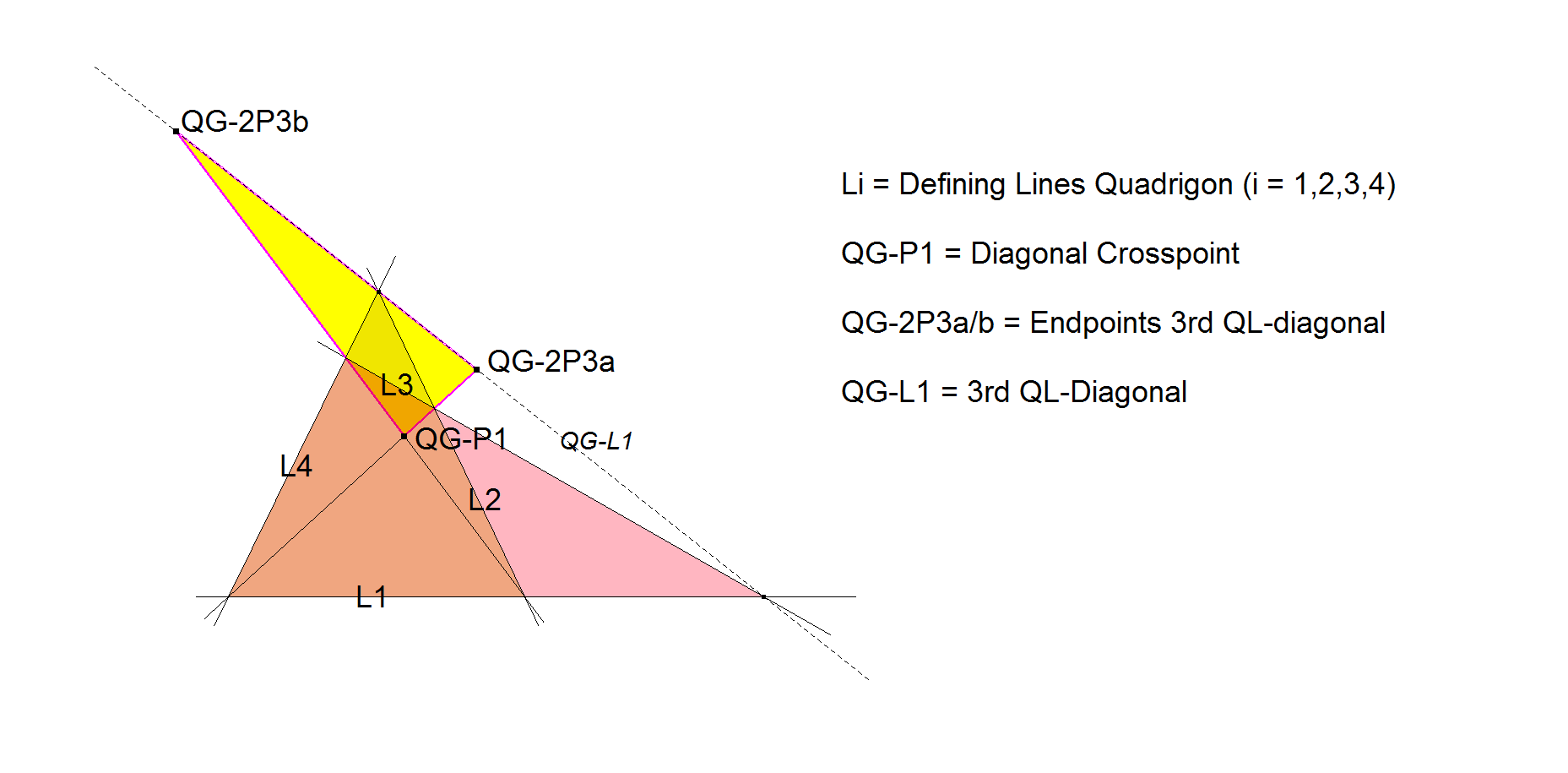
In a Quadrigon (system of 4 consecutive lines L1, L2, L3, L4) the Diagonal Triangle of a Quadrilateral (system of 4 lines unrestricted) can be seen as a triangle with these vertices:
When the Quadrigon vertices are P1, P2, P3, P4 in this order, then:
- QG-P1 = intersection point (L4.L1^L2.L3) ^ (L1.L2^L3.L4)
- QG-2P3a = intersection point L1^L3
- QG-2P3b = intersection point L2^L4.
Coordinates:
CT-coordinates QA-2P3a/b in 1st QA-Quadrigon:
QG-2P3a: (p : 0 : -r)
QG-2P3b: (p : 2 q : r)
CT-coordinates QA-2P3a/b in 1st QL-Quadrigon:
QG-2P3a: (p : 0 : -r)
QG-2P3b: (p : 0 : r)
DT-coordinates QA-2P3a/b in 1st QA-Quadrigon:
QG-2P3a: (-m n : -l n : l m)
QG-2P3b: (-m n : l n : l m)
DT-coordinates QA-2P3a/b in 1st QL-Quadrigon:
QG-2P3a: (0 : 0 : 1)
QG-2P3b: (1 : 0 : 0)
Properties:
- QG-2P3a and QG-2P3b are collinear with QG-P2, QG-P3 and QG-2P2a/b.
- QG-2P3a and QG-2P3b are each other’s Reflection in QG-P3.
- QG-2P3a and QG-2P3b define the line segment which is the diameter of QG-Ci2 (QL-DT-Thales Circle).
- Let L3a and L3b be the lines through QG-2P3a and QG-2P3b parallel to QG-P1.QA-P16. Let L2a, L2b and L2c be the sidelines of the QA-Diagonal Triangle, L2c being the 3rd diagonal QG-L1. The pairs of triangles (L2a,L2c,L3a) and (L2b,L2c,L3a) as well as (L2a,L2c,L3b) and (L2b,L2c,L3b) have equal areas. See Ref-50, ADGEOM #2380/2382, Tsihong Lau, where L3a and L3b are called area equalizers.