QG-2P6: Outer and Inner Van Aubel Points
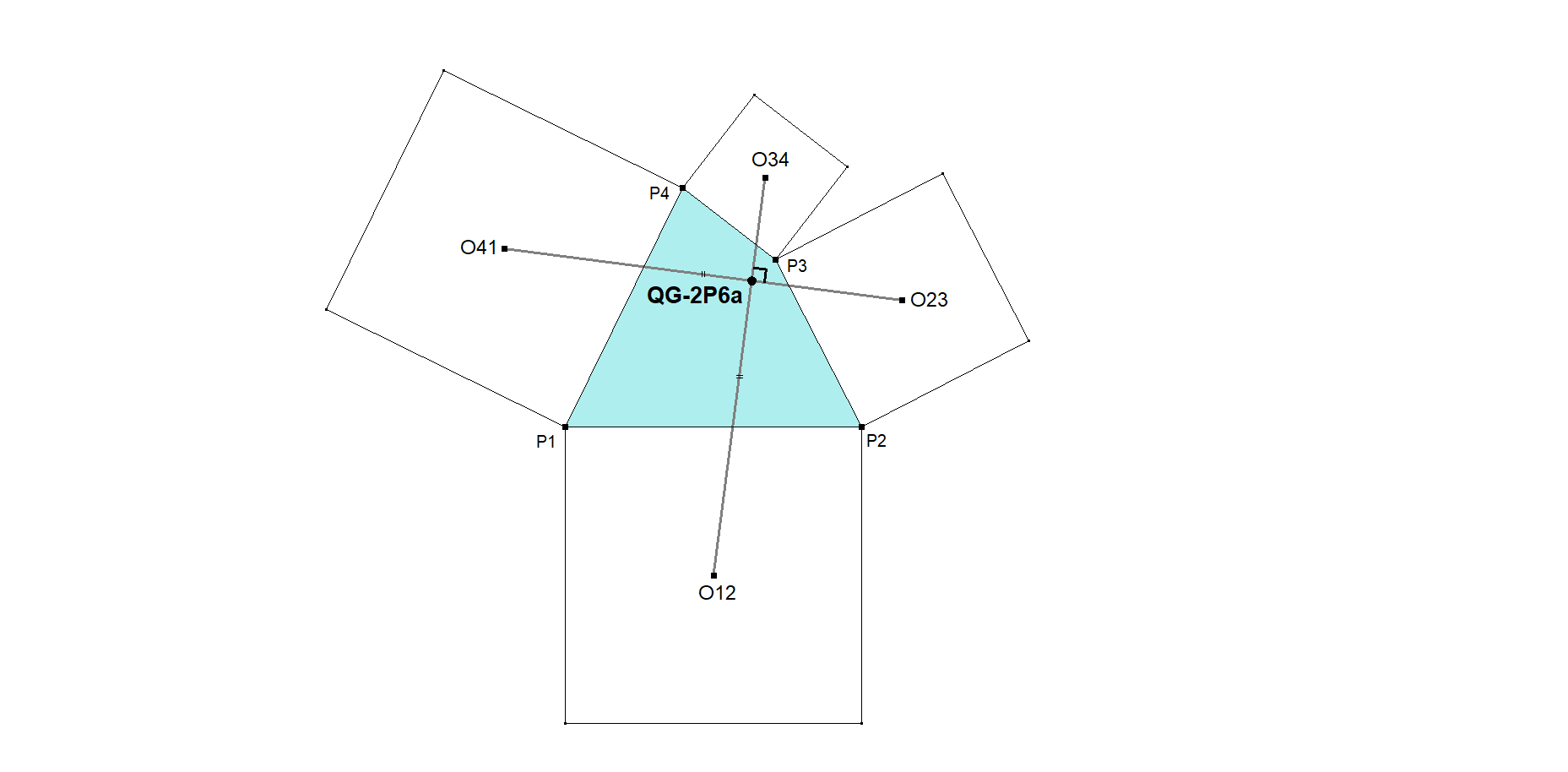
Let P1.P2.P3.P4 be a Quadrigon.
Erect an outward square at line segment P1.P2. Let O12 be its center.
Similarly construct outward squares at line segments P2.P3, P3.P4, P4.P1 resp. with centers O23, O34, O41.
Van Aubel discovered that line segments O12.O34 and O23.O41 are equal of length and mutually perpendicular. The intersection point of O12.O34 and O23.O41 is QG-2P6a, the Outer Van Aubel Point
When the inward squares at the edges of the Quadrigon are erected the same properties occur and the intersection point of O12.O34 and O23.O41 is QG-2P6b, the Inner Van Aubel Point.
See also [8], Aubel, Stelling van Van, and [13] Van Aubel’s Theorem, and [74].
Properties
- QG-2P6a and QG-2P6b are also the centers of the two Circumscribed Squares of a Quadrigon. For a proof see [73]. See also [34], QFG#372.
- QA-P2 of the Reference Quadrigon lies on the perpendicular bisector of QG-2P6a .QG-2P6b.
- QG-2P6a and QG-2P6b have the same distance d to the Centroid QA-P1 of the Reference Quadrigon. In a Quadrilateral there are 3 distances per QL-Quadrigon: da, db, dc. Then da + db + dc = 0. (distances are signed).
- QG-2P6a and QG-2P6b lie on the Thales Circle of the midpoints of the two diagonals of the Reference Quadrigon (note Eckart Schmidt 2012, September 18).
Estimated human page views: 456
