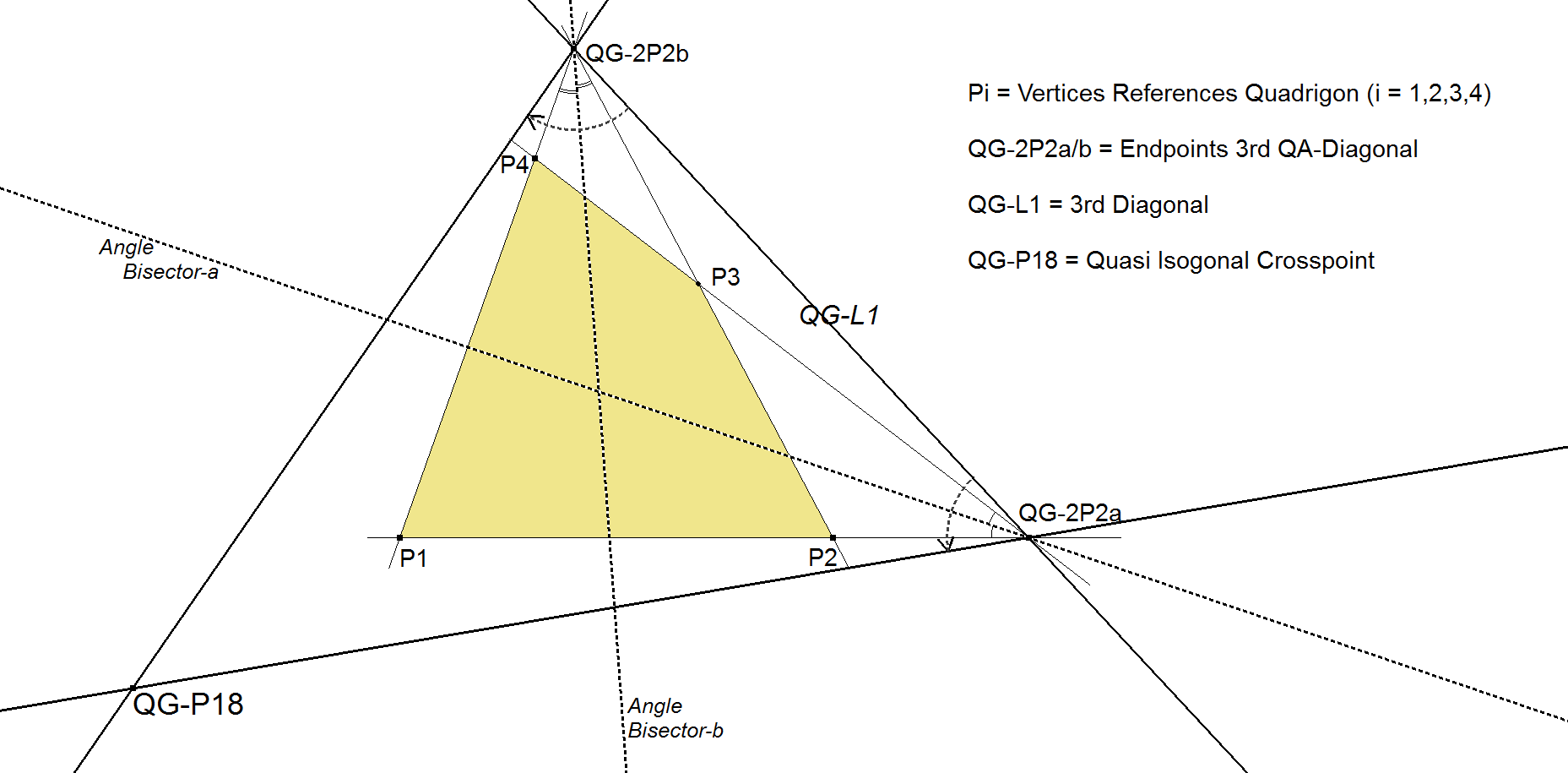
QG-P18: Quasi Isogonal Crosspoint
QG-P18 is the intersection of the reflections of the 3rd Diagonal QG-L1 in the angle bisectors of the opposite sides of the quadrigon.
This point and its properties are found by Eckart Schmidt (October 5, 2012).
CT-Coordinates in 1st QA-Quadrigon
(-a2 q r ((p + q) (b2 p + a2 q) r2 – c2 p q (p q + r2)) :
-p r (b4 p (p + q) r (q + r) – (a2 – c2) q2 (a2 (p + q) r – c2 p (q + r)) + b2 q (-a2 (p + q) (p – q – r) r + c2 p (p + q – r) (q + r))) :
-c2 p q (c2 p2 q (q + r) + r (b2 p2 (q + r) – a2 q (p2 + q r))))
DT-Coordinates in 1st QA-Quadrigon
((a2 – b2 – c2) (b2 p2 + a2 q2) :
-(a2 – b2 – c2) (a2 + b2 – c2) q2 :
-(a2 + b2 – c2) (c2 q2 + b2 r2))
CT-Coordinates in 1st QL-Quadrigon
(a2 l (a2 (l – m) (l – n) + c2 (l – n) (m – n) – b2 (l m – l n + m n)) :
b2 m (a2 l2 – c2 n2) :
c2 n (-a2 (l – m) (l – n) + c2 (l – n) (-m + n) + b2 (l m – l n + m n)))
DT-Coordinates in 1st QL-Quadrigon
(a4 (l2 – n2) + b2 (b2 – c2) (m2 – n2) + a2 (c2 (-l2 + n2) + b2 (l2 + m2 + 2 n2)) :
a4 (-l2 + n2) + b4 (-l2 + n2) + c4 (-l2 + n2) + 2 b2 c2 (l2 + n2) – 2 a2 (c2 (-l2 + n2) + b2 (l2 + n2)) :
b4 (l2 – m2) + c4 (l2 – n2) – b2 c2 (2 l2 + m2 + n2) + a2 (b2 (-l2 + m2) + c2 (-l2 + n2)))
Properties
- QG-P18 lies on the line through QG-2P5a and QG-2P5b, the intersection points of the QL-DT-Thales Circle (QG-Ci2) with the QG-Diagonals.
- Let Si = QG-P1, Xi = QG-P18 and Yi = QG-P19 resp. in QA-Quadrigon-i (i=1,2,3). Now Si.Xj ^ Sj.Xi = Yk, Si.Yj ^ Sj.Yi = Xk, Xi.Yj ^ Xj.Yi = Sk.
- The Triangles formed by the QA-versions of QG-P1, QG-P18 and QG-P19 are pairwise perspective triangles. Their centers of perspectivity are collinear.
- The Quasi Isogonal Conjugate (QG-Tf2) wrt the Reference Quadrigon is equivalent to the Isogonal Conjugate wrt the Triangle QG-2P2a.QG-2P2b.QG-P18.
- The QG-Tf2 image (Quasi Isogonal Conjugate) of a free line is a conic through QG-P18.
- The QG-Tf2 image (Quasi Isogonal Conjugate) of any point on QG-L1 is QG-P18.
- The QA-Tf2 image (Involutary Conjugate) of QG-P18 is QG-P19.
- QG-P18 is the QL-Tf1 image (Clawson-Schmidt Conjugate) of QG-P17.
- QG-P18 lies concyclic with QG-2P2a, QG-2P2b and QL-P1 (as 4th intersection of the circle and QL-Cu1).
- QA-P41 lies on the circle defined by the 3 QA-versions of QG-P18.
- The 3 QA-versions of QG-P18 lie on QA-Cu7.
- The 3 QL-versions of QG-P18 are collinear points on QL-Cu1.
- QG-P18 is the second focus of an inscribed conic with its first focus in QG-P17.
- Perpendiculars from QG-P18 to the sidelines of the quadrigon have pedal points on a circle, which is centered in the midpoint of QG-P17 and QG-P18 (this midpoint is a point on the Newton Line QL-L1).
- QG-P18 lies on the Polar (see [13], Polar) of QG-P19 wrt any circumscribed conic of the Reference Quadrigon.
- The Triple Triangle of QG-P18 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).
- QG-P18 is the common tangential of QG-2P2a,b wrt QL-Cu1. See [66], QPG-message 485.
Estimated human page views: 482
