QG-P5: 1st QG-Quasi Circumcenter
The 1st QG-Quasi Circumcenter is the Diagonal Crosspoint of the X3-Quadrigon.
The X3-Quadrigon is defined by its vertices being the Triangle Circumcenters of the component triangles of the Reference Quadrigon.
This point and other 1st quasi points are described in Ref-5.
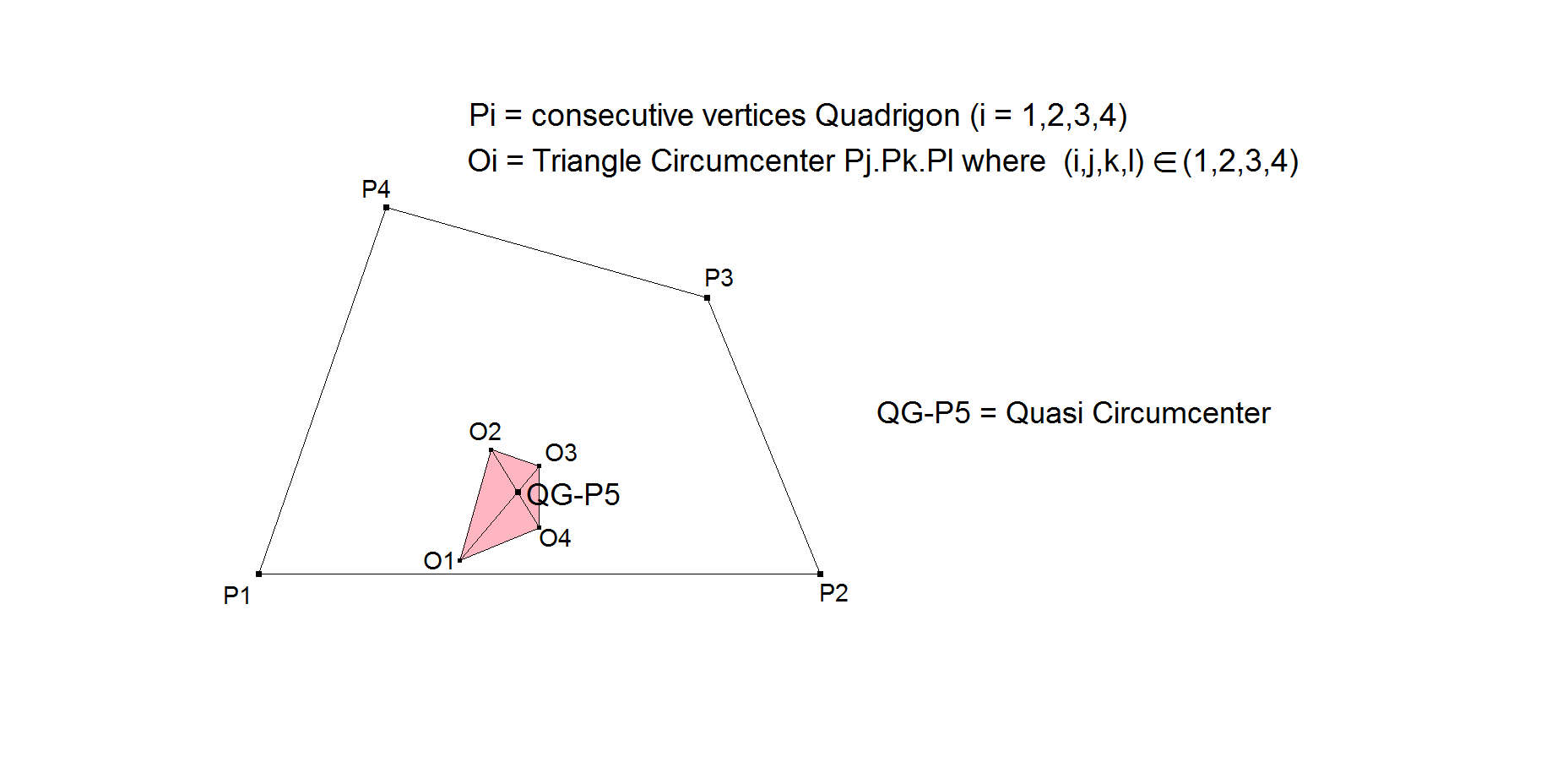
As can be seen in next picture, there are more special properties about this point:
Coordinates:
CT-coordinates QG-P5 in 3 QA-Quadrigons: (only coordinates of 1st Quadrigon point are given)
- (a2 SA (p2 + r2) - (a2 + c2) SC p r - (a2 - c2) SB p q - a2 (a2 - c2) q r + 8 Δ2 p r :
b2 SB ( p2 + q r + r2 + p q) + a2 b2 r (p + q) + b2 c2 p (q + r) :
c2 SC (p2 + r2) - (a2 + c2) SA p r + (a2 - c2) SB q r + c2 (a2 - c2) p q + 8 Δ2 p r)
CT-coordinates QG-P5 in 3 QL-Quadrigons: (only coordinates of 1st Quadrigon point are given)
- (b2 c2 l m (m - n)2 - c4 l m (m - n)2 + a4 (l - m) (l m2 + l n2 - m n2)
+ a2 (-b2 (l - m) (l m2 - 2 l m n + 2 m2 n + l n2 - m n2) + c2 (-l2 m2 + 2 l m3 + 2 l2 m n - 2 l m2 n - l2 n2 + l m n2 - m2 n2)) :
- a4 (l - m)l m n + c4 l m (m - n) n + b4(l - m) (m - n) (l m - l n + m n)
- b2c2(m - n) (l2 m + l m2 - l2 n + l m n - m2 n) + a2 (c2 l m n (l - 2 m + n) - b2 (l - m) (l m2 - l m n - m2 n + l n2 - m n2)) :
- a4 (l - m)2 m n + c4 (m - n) (l2 m - l2 n - m2 n) - b2 c2 (m - n) (l2 m - 2 l m2 - l2 n + 2 l m n - m2 n)
+ a2 (b2 (l - m)2 m n + c2 (-l2 m2 + l2 m n - 2 l m2 n + 2 m3 n - l2 n2 + 2 l m n2 - m2 n2)))
CT-Area of QG-P5-Triangle in the QA-environment: (equals 4x area QA-Morley Triangle)
- (c2 p q + b2 p r + a2 q r)2 / (8 Δ (p + q) (p + r) (q + r) (p + q + r))
CT-Area of QG-P5-Triangle in the QL-environment:
- ((a2 m n (l-m) (l-n) (lm-mn+ln) + b2 n l (m-l) (m-n) (lm+mn-ln) + c2 l m (n-l) (n-m) (-lm+mn+ln))2)
/ (16 Δ (l - m)2 (l - n)2 (m - n)2 (-lm+ln+mn) (lm+ln-mn) (lm-ln+mn))
DT-coordinates QG-P5 in 3 QA-Quadrigons: (only coordinates of 1st Quadrigon point are given)
- (2 Sb (Sa p2+Sb q2) (p2-r2)+Sc (p2-q2-r2) (Sa p2+Sc r2)+Sb Sc (p4-p2 q2-3 q2 r2-r4) :
Sa (Sa p2+Sb q2) (p2+q2-r2)+Sc (-p2+q2+r2) (Sb q2+Sc r2)-Sa Sc q2 (p2-q2+r2) :
-2 Sb (p2-r2) (Sb q2+Sc r2)-Sa (p2+q2-r2) (Sa p2+Sc r2)-Sa Sb (p4+3 p2 q2+q2 r2-r4))
DT-coordinates QG-P5 in 3 QL-Quadrigons: (only coordinates of 1st Quadrigon point are given)
- (a2 m2 (c2 n2-Sa m2-Sb l2) : m2 (Sb Sc l2+Sa Sc m2+Sa Sb n2)-S2 l2 n2 : c2 m2 (a2 l2-Sc m2-Sb n2))
DT-Area of QG-P5-Triangle in the QA-environment: (equals 4x area QA-Morley Triangle)
- (Sa p2 + Sb q2 + Sc r2)2 / (2 S (-p+q+r) (p+q-r) (p-q+r) (p+q+r))
DT-Area of QG-P5-Triangle in the QL-environment:
- (Sc (l2-m2)2 n2 + Sb (l2-n2)2 m2 + Sa (m2-n2)2 l2)2 / (2 S (l2-m2)2 (l2-n2)2 (m2-n2)2)
Properties:
- QG-P4, QG-P5, QG-P6, QG-P7 are collinear on QG-L4, the 1st QG-Quasi Euler Line.
- QG-P5 is the Reflection of QG-P1 in QG-P9 and the Reflection of QG-P6 in QG-P7.
- QG-P5 is the Reflection of QA-P24 in QL-P2 (Eckart Schmidt, July, 2012).
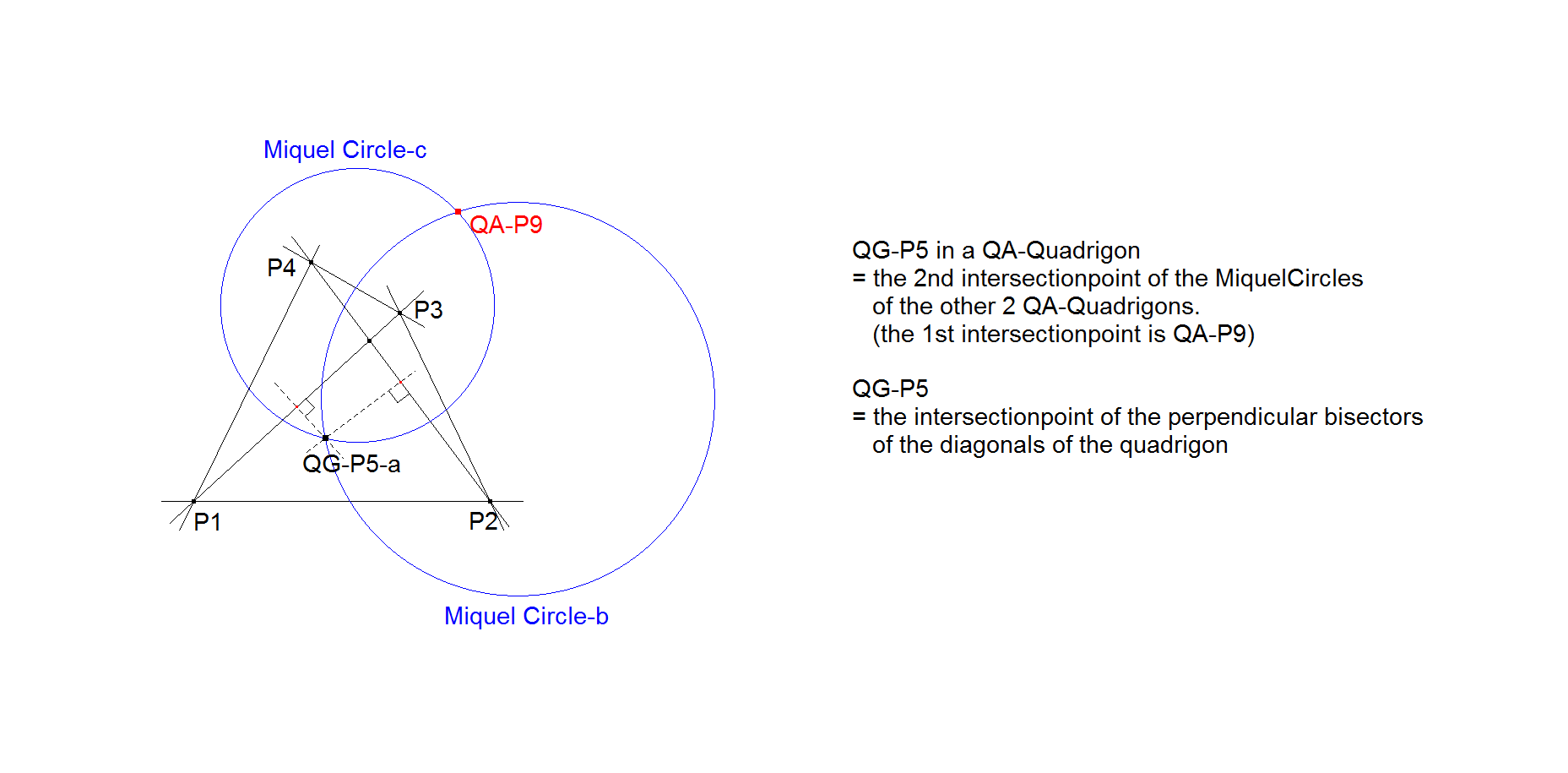
- QG-P5 is the intersection point of the perpendicular bisectors of the diagonals.
- QG-P5 in a QA-Quadrigon = the 2nd intersectionpoint of the MiquelCircles (QL-Ci3) of the other 2 QA-Quadrigons (the 1st intersectionpoint is QA-P9).
- The three QA-versions of QG-P5 lie on a circle through QA-P3, centered in the reflection of QA-P15 in QA-P1. See Ref-34, Eckart Schmidt, QFG#1263.
- In a Quadrangle the QG-P5-Triangle is perspective with the QL-P1-Triangle (QA-Tr2). Their perspector is not registered in EQF.
- In a Quadrangle the QG-P5-Triangle is perspective and homothetic with the QL-P2-Triangle (QA-Tr3). The area of the 1st Triangle equals 4x the area of the 2nd Triangle. Their perspector is QA-P24.
- In a Quadrilateral the sides of the QG-P5-Triangle pass through the midpoints of the 3 QL-Diagonals at the Newton Line (QL-L1).
- QA-P3 (Gergonne-Steiner Point) lies on the circumcircle of the triangle formed by the 3 QA-versons of QG-P5.
- QL-P16 as well as QL-P17 lie on the circle defined by the 3 QL-versions of QG-P5 and on the circle defined by the 3 QL-versions of QG-P9. Moreover the center of the circle defined by the 3 QL-versions of QG-P5 lies on the circle defined by the 3 QL-versions of QG-P9.
-
The sidelines of the triangle formed by the 3 QA-versions of QG-P5 are the loci of points P where d12 + di2 = dj2 + dk2 ( (i,j,k) ∈ (2,3,4) ), where di = distance (P, Pi).
- The QA-Orthopole (QA-Tf3) of QG-P5 is QG-P7.
- The QA-Möbius Conjugate (QA-Tf4) of QG-P5 is QL-P1.
- Let M13, M24 be the Midpoints of P1.P3 and P2.P4. Let O = QG-P5. Now the two angles between the lines O.M13 and O.M24 correspond with (Angle P1.O.P2 + Angle P3.O.P4)/2 and (Angle P2.O.P3 + Angle P4.O.P1) /2. See Ref-34, QFG messages #417,418.
- The QG-P5 Triple Triangle in a Quadrangle is Orthologic wrt all QA-Component Triangles (Seiichi Kirikami, Ref-34, QFG #980, # 982). See QA-Tr-1.