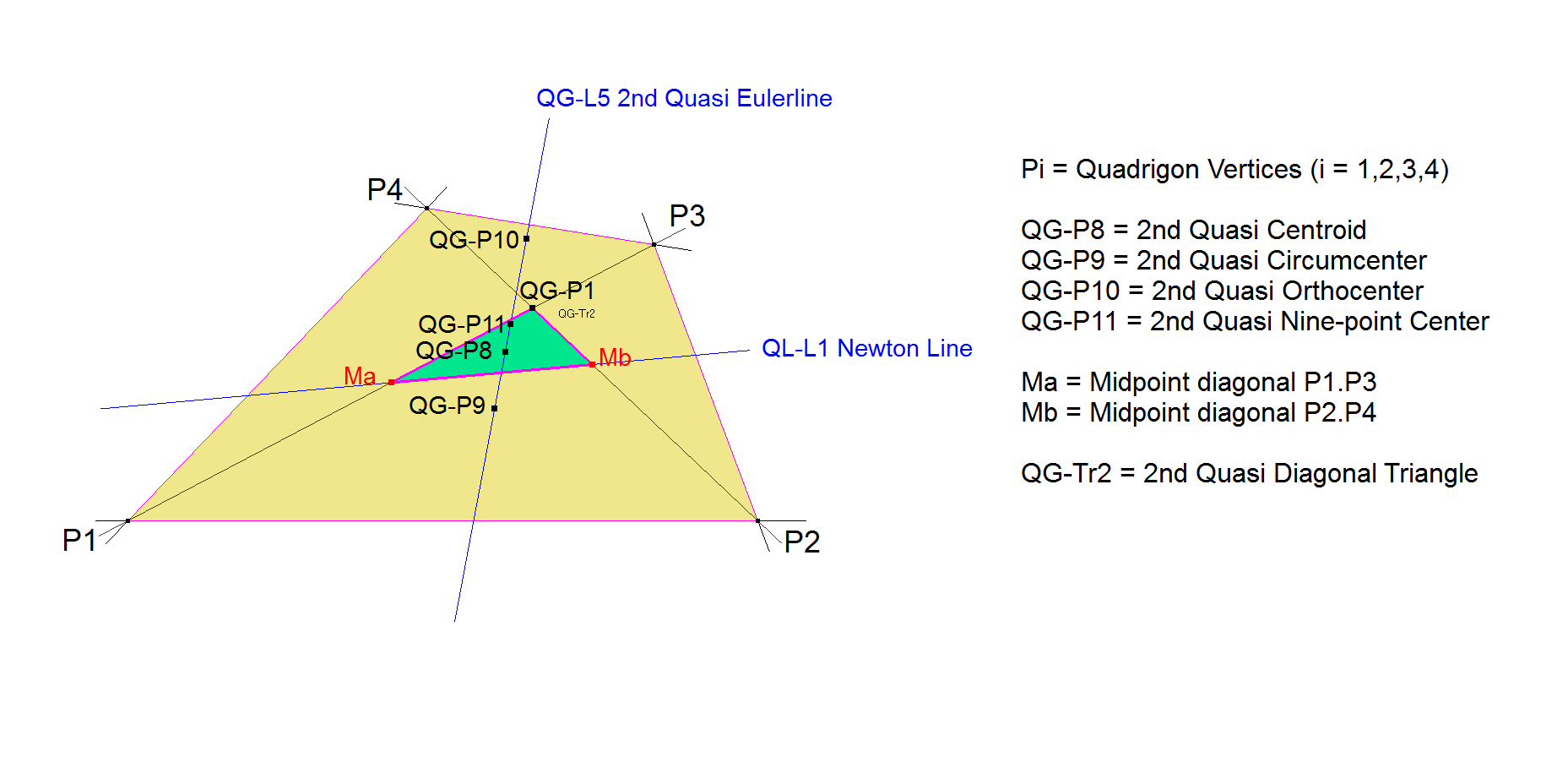
QG-Tr2: 2nd QG-Quasi Diagonal Triangle
QG-Tr2 is the Triangle with vertices QG-P1 (Diagonal Crosspoint) and the midpoints of the 2 diagonals of the Reference Quadrigon.
Special about this triangle is that the 2nd Quasi points QG-P8, QG-P9, QG-P10, QG-P11 are the corresponding triangle points of this Triangle.
For example the 2nd Quasi Centroid QG-P8 of the Reference Quadrigon is also the Triangle Centroid of QG-Tr2.
Area QG-2nd Diagonal Triangle in 3 QA-Quadrigons CT-notation
(r – p) (p + 2 q + r) S / (8 (p + r) (p + q + r))
(r – q) (2 p + q + r) S / (8 (q + r) (p + q + r))
(p – q) (p + q + 2 r) S/ (8 (p + q) (p + q + r))
Area QG-2nd Diagonal Triangle in 3 QL-Quadrigons CT-notation
(-l m + l n + m n) (l m + l n – m n) S / (8 (m – l) (m – n) ( l m – l n + m n))
( l m – l n + m n) (l m + l n – m n) S / (8 (n – l) (n – m) (-l m + l n + m n))
(-l m + l n + m n) (l m – l n + m n) S / (8 (l – m) ( l – n) ( l m + l n – m n))
–
Area QG-2nd Diagonal Triangle in 3 QA-Quadrigons DT-notation
p r (p – r) (p + r) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))
q r (q – r) (q + r) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))
p q (q – p) (q + p) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))
Area QG-2nd Diagonal Triangle in 3 QL-Quadrigons DT-notation
m4 S / (2 (m2 – l2) (m2 – n2))
n4 S / (2 ( n2 – l2) (n2 – m2))
l4 S / (2 ( l2 – m2) ( l2 – n2))
Properties
- The 2nd QG-Quasi Euler line QG-L5 is also the Triangle Euler line of QG-Tr2.
- The points 2nd Quasi Centroid/Circumcenter/Orthocenter/Nine-point Center (resp. QG-P8, QG-P9, QG-P10, QG-P11) are also the Centroid/Circumcenter/ Orthocenter/Nine-point Center of QG-Tr2.
- When the Reference Quadrigon is cyclic the Maltitudes (a Maltitude is a line drawn from the midpoint of a side perpendicular to the opposite side of a Quadrigon) concur in the orthocenter QG-P10 of QG-Tr2. This point in a cyclic Quadrigon is also known as the Anticenter.
Estimated human page views: 505
