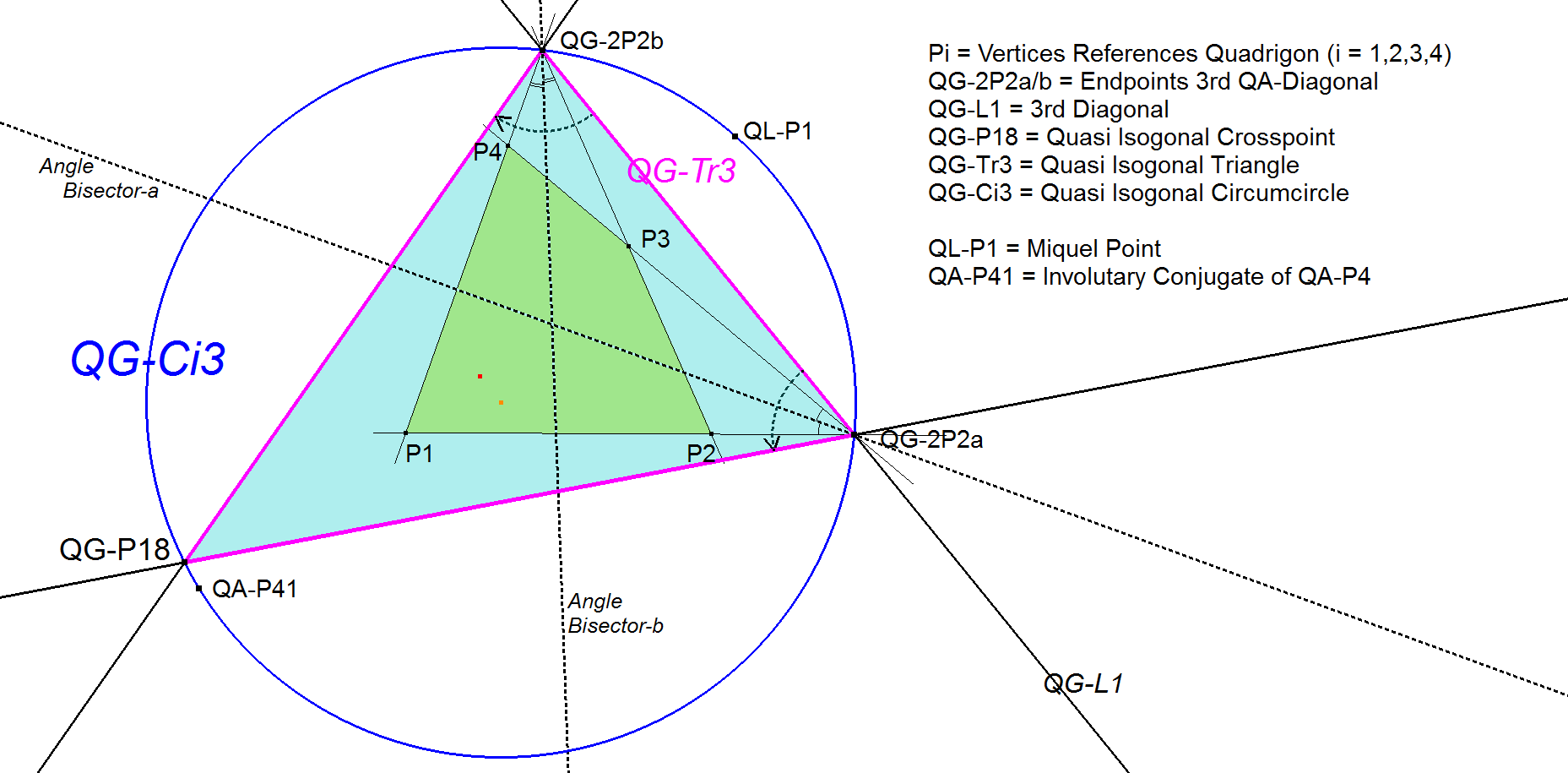
QG-Tr3: Quasi Isogonal Triangle
QG-Tr3 is defined by 3 lines: the 3rd Diagonal and its Reflections in the Angle Bisectors of the two sets of opposite lines in the Reference Quadrigon.
So the vertices are the two Endpoints of the QA-3rd Diagonal (QG-2P2a/b) and the Quasi Isogonal Crosspoint (QG-P18).
There are two major properties that make this Triangle important:
The Quasi Isogonal Conjugate (QG-Tf2) as defined in a Quadrigon is equivalent to the Isogonal Conjugate of QG-Tr3.
The Circumcircle of this Triangle when “tripled” in a Quadrangle as well as in a Quadrilateral, causes three circles that concur in one single point (resp. QA-P41 and QL-P1). See also QG-Ci3.
Area QG-Tr3 in 1st QA-Quadrigon CT-notation
((c2 p2 q2 – a2 p2 q r + b2 p2 q r + c2 p2 q r + b2 p2 r2 – a2 q2 r2) (c2 p2 q2 – b2 p2 r2 – a2 p q r2 – b2 p q r2 + c2 p q r2 – a2 q2 r2) Δ
/ ((p + q) (q + r) (c2 p q + b2 p r + a2 q r) (c2 p2 q2 – a2 p2 q r + b2 p2 q r + c2 p2 q r – a2 p q2 r + b2 p q2 r – c2 p q2 r + b2 p2 r2 + a2 p q r2 + b2 p q r2 – c2 p q r2 + a2 q2 r2))
Area QG-Tr3 in 1st QL-Quadrigon CT-notation
((a l – c n) (a l + c n) (a2 l2 – a2 l m – b2 l m + c2 l m – a2 l n + b2 l n – c2 l n + a2 m n – b2 m n – c2 m n + c2 n2) Δ
/ ((l – n) (a2 l – a2 m + c2 m – c2 n) (a2 l2 – a2 l n + b2 l n – c2 l n + c2 n2))
Area QG-Tr3 in 1st QA-Quadrigon DT-notation
((a2 – b2 – c2) (a2 + b2 – c2) q2 Δ
/ (b2 (-a2 p2 + b2 p2 + c2 p2 + a2 q2 – b2 q2 + c2 q2 + a2 r2 + b2 r2 – c2 r2))
Area QG-Tr3 in 1st QL-Quadrigon DT-notation
(l n (a2 l + b2 l – c2 l + a2 n – b2 n – c2 n) (a2 l + b2 l – c2 l – a2 n + b2 n + c2 n) Δ
/ (b2 (l – n) (l + n) (a2 l2 – a2 m2 + c2 m2 – c2 n2))
Properties
- The Quasi Isogonal Conjugate (QG-Tf2) as defined in a Quadrigon is equivalent to the Isogonal Conjugate of QG-Tr3.
- The Circumcircle of this Triangle is the only known QG-Circle that, when “tripled” in a Quadrangle as well as in a Quadrilateral, causes three circles that concur in one single point (resp. QA-P41 and QL-P1). See also QG-Ci3.
Estimated human page views: 814
