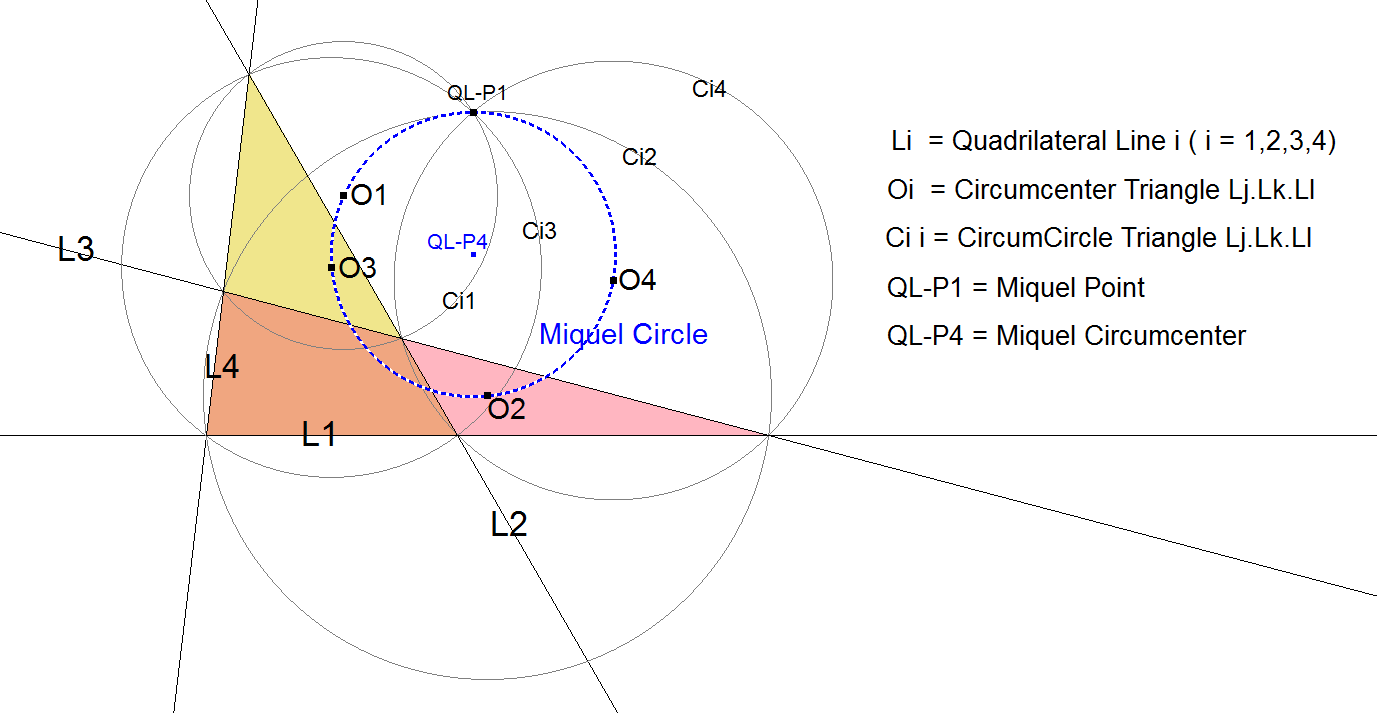
QL-Ci3: Miquel Circle
The circumcenters of the 4 Component Triangles of a Quadrilateral are concyclic and lie on QL-Ci3, the Miquel Circle. QL-P4 is its center.
Suppose four lines intersect two by two at six points.
(1) These four lines, taken three by three, form four triangles whose circumcircles
pass through the same point F.
(2) The centers of the four circles (and the point F) lie on the same circle.
(see Jean-Pierre Ehrmann Ref-4, page 35).
This circle is called the circumcentric circle by J.W. Clawson. See Ref-22, page 250.
He appoints 47 points on this circle, which is the Miquel Circle.
Equation/Radius:
Equation in CT-notation:
(x + y + z) (b2 c2 l (m - n) TA x + c2 a2 m (n - l) TB y + a2 b2 n (l - m) TC z) – TAL (a2 y z + b2 z x + c2 x y) = 0
where:
TA = - 2 a2 l + 2 SC m + 2 SB n
TB = - 2 b2 m +2 SA n + 2 SC l
TC = - 2 c2 n + 2 SB l + 2 SA m
TAL = (a - b - c) (a + b - c) (a - b + c) (a + b + c) (l - m) (l - n) (m - n)
Radius2 of Circle in CT-notation:
(a2 (l - m) (l - n) + b2 (m - l) (m - n) + c2 (n - l) (n - m))
* (a2 m n (l - m) (l - n) + b2 l n (m - l) (m - n) + c2 l m (n - l) (n - m))
* a2 b2 c2 / (256 Δ4 (l - m)2 (l - n)2 (m - n)2)
where: Δ = Area = 1/4 √[(a + b + c) (-a + b + c) (a - b + c) (a + b - c)]
Properties:
- QL-Ci3 plays a role in QA-P9 (Miquel Center).
- QL-Ci3 has the same radius as the Hervey Circle (QL-Ci4).
- QL-Ci3 is the Reflection of QL-Ci4 in QL-P5.
- QL-Ci3 is the Clawson-Schmidt Conjugate (QL-Tf1) of the Steiner Line (QL-L2). As a consequence the Clawson-Schmidt Conjugates of QL-P2, QL-P7 and QL-P9 lie on QL-Ci3.
- The 2nd intersection point of QL-Ci3 with the circumcircle of a Component Triangle Li.Lj.Lk is Incenter or Excenter of the Triangle formed by the Reflections of Li, Lj, Lk in Ll, where (i,j,k,l) ∈ (1,2,3,4). See Ref-33 Anopolis message # 431.
-
Let Ti = Triangle formed by the 3 lines Lij, Lik, Lil ((i,j,k,l) ∈ (1,2,3,4)) where Lmn = Line perpendicular to Ln at intersection point Lm^Ln. The circumcenters of the 4 triangles Ti (i=1,2,3,4) lie on QL-Ci3. Moreover the circumcircles of the 4 triangles Ti (i=1,2,3,4) have one common point, being QL-P1. Found by Antreas P. Hatzipolakis, see Ref-33, Anopolis messages #466, #467.
- Let O1, O2, O3, O4 be the 4 circumcenters of the 4 QL-Component Triangles. The Ninepoint Conic QA-Co1 of Quadrangle O1.O2.O3.O4 is an Orthogonal Hyperbola through QL-P4 and QL-P5 with center QL-P6 and axes parallel to the Steiner Axes (see QL-Tf1). See Ref-34, QFG-messages #1544,#1545.
- Let O1, O2, O3, O4 be the 4 circumcenters of the 4 QL-Component Triangles. The Orthogonal Hyperbola QA-Co2 of Quadrangle O1.O2.O3.O4 also passes through the points H1,H2,H3,H4 of QL-Ci4 and is tangent to the QL-inscribed conic with center QL-P5 in two points which are collinear with QL-P1 and QL-P5. See Ref-34, QFG-messages #1539-1545.