QL-Ci4: Hervey Circle

---

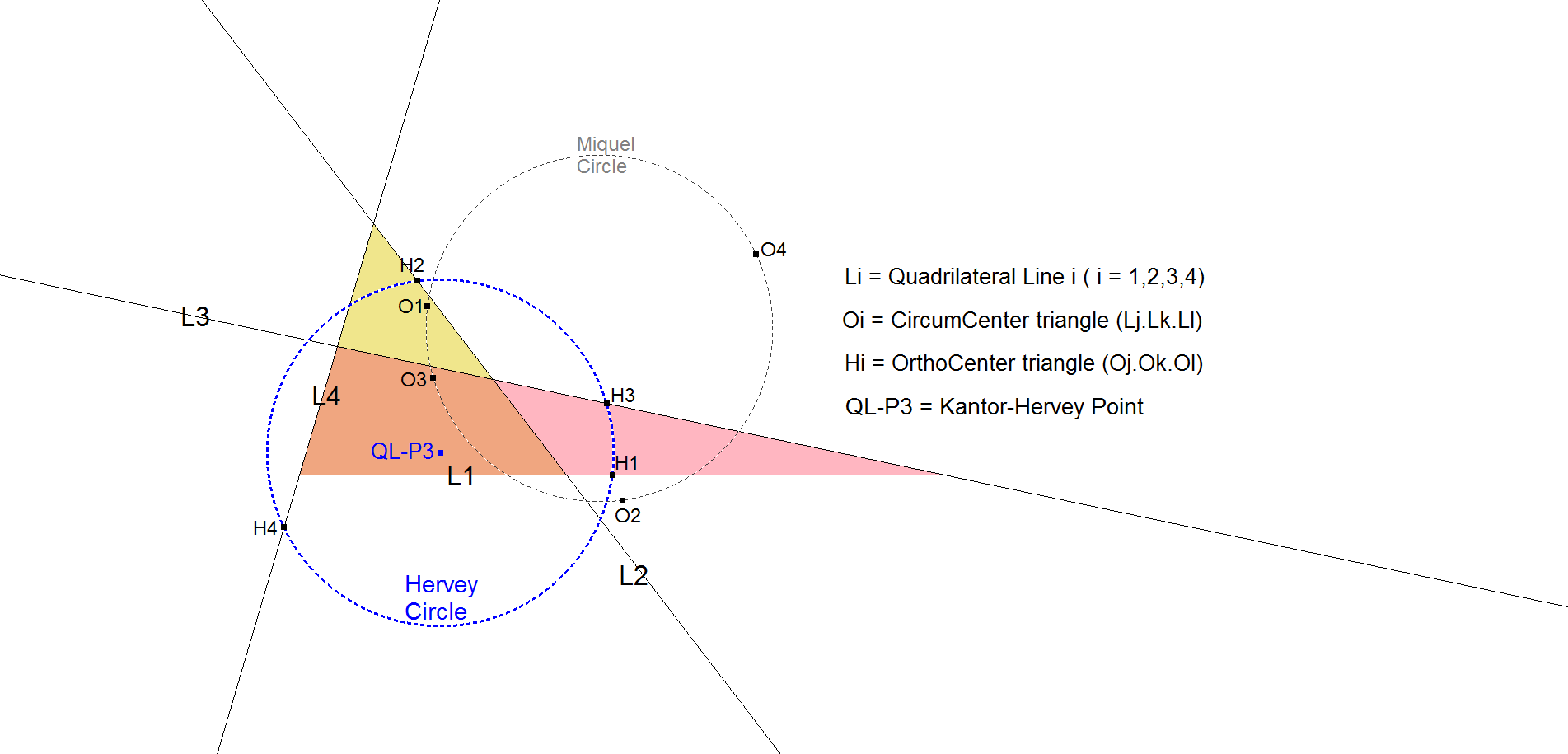
Let Hi (i=1,2,3,4) be the Orthocenters of the 4 component triangles of the Quadrangle formed by the Circumcenters of the 4 component triangles of the Reference Quadrilateral.

These 4 Orthocenters lie on one of the 4 defining Lines of the Reference Quadrilateral and are concyclic. The circle through these points is the Hervey Circle.

QL-P3 (Kantor-Hervey Point) is its center.

 

 

Equation/Radius:          

Equation in CT-notation:

2 (x + y + z) (A_M A_N S_A x + B_L B_N S_B y + C_M C_L S_C z) - T_AL² (c² x y +b² x z + a² y z) = 0

where:

A_M = +a⁴ m(l-m)(l-n) + b⁴ l (l-m)(m-n) + c⁴ l (l-n)(m-n) - b² c² (m-n) l (2l-m-n)  +  a² c² (l-n)(m²+ln-2mn) - a² b² (l-m)(2lm-ln-mn)

A_N = -a⁴ n(l-m)(l-n)   + b⁴ l (l-m)(m-n) + c⁴ l (l-n)(m-n)  - b² c² (m-n) l (2l-m-n)  -  a² c² (l-n)(l m-2ln+mn) - a² b² (l-m)(lm-2mn+n²)

B_L = -a⁴ m(l-m)(l-n)  - b⁴ l(l-m)(m-n)   + c⁴ m(l-n)(m-n) + b² c² (m-n)(l²-2ln+mn) + a² c² (l-n) m (l-2m+n) + a² b² (l-m)(2lm-ln-mn)

B_N = -a⁴ m(l-m)(l-n) + b⁴ n(l-m)(m-n) + c⁴ m(l-n)(m-n) - b² c² (m-n)(lm+ln-2mn) + a² c² (l-n)m(l-2m+n) + a² b² (l-m)(lm-2ln+n²)

C_M = +a⁴ n(l-m)(l-n) + b⁴ n(l-m)(m-n) + c⁴ m(l-n)(m-n) - b² c² (m-n)(lm+ln-2mn) + a² c² (l-n)(2lm-m²-ln)  - a² b² (l-m)n(l+m-2n)

C_L = +a⁴ n(l-m)(l-n)  + b⁴ n(l-m)(m-n) - c⁴  l (l -n)(m-n) + b² c² (m-n)(l²-2lm+mn) + a² c² (l-n)(lm-2ln+mn) - a² b² (l-m)n(l+m-2n)

T_AL = (a - b - c)(a + b - c)(a - b + c)(a + b + c) (l - m)(l - n)(m - n)

Radius² of Circle in CT-notation:                 

   (a²         (l - m) (l - n) + b²       (m - l) (m - n) + c²       (n - l) (n - m))

* (a² m n (l - m) (l - n) + b² l n (m - l) (m - n) + c² l m (n - l) (n - m))

*   a² b² c²   /   (256 Δ⁴ (l - m)² (l - n)² (m - n)²) 

where:  Δ = Area = 1/4 √[(a + b + c) (-a + b + c) (a - b + c) (a + b - c)]

Properties:

• QL-P3 is the Center of QL-Ci4.
• The Reflection of QL-P1 in QL-P5 lies on QL-Ci4 (Bernard Keizer, March 28, 2013).
• The Hervey Circle has the same radius as the Miquel Circle (QL-Ci3).
• The Hervey Circle is the Reflection of QL-Ci3 in QL-P5.
• Let (L1,L2,L3,L4) be a quadrilateral. H1 is orthocenter of triangle (L2,L3,L4). K1 is orthopole of L1 wrt triangle (L2,L3,L4). X1 lies on L1 such that X1K1 is perpendicular to K1H1. Similarly X2,X3,X4 are constructed. Then X1,X2,X3,X4 lie on QL-Ci4. See Ref-34, Tran Quang Hung, QFG#2075.

---