QL-L10: QL-LSD Line
QL-L10 is the line with Least Sum of Squared Distances of the QL-vertices (6 intersection points of the 4 QL-lines) to this line.
Construction
Next construction uses properties of the Complex Plane. It is the same type of construction as used for QA-L10. This type of construction can be used for any number of points. See [34], QFG-messages #1585, #1590.
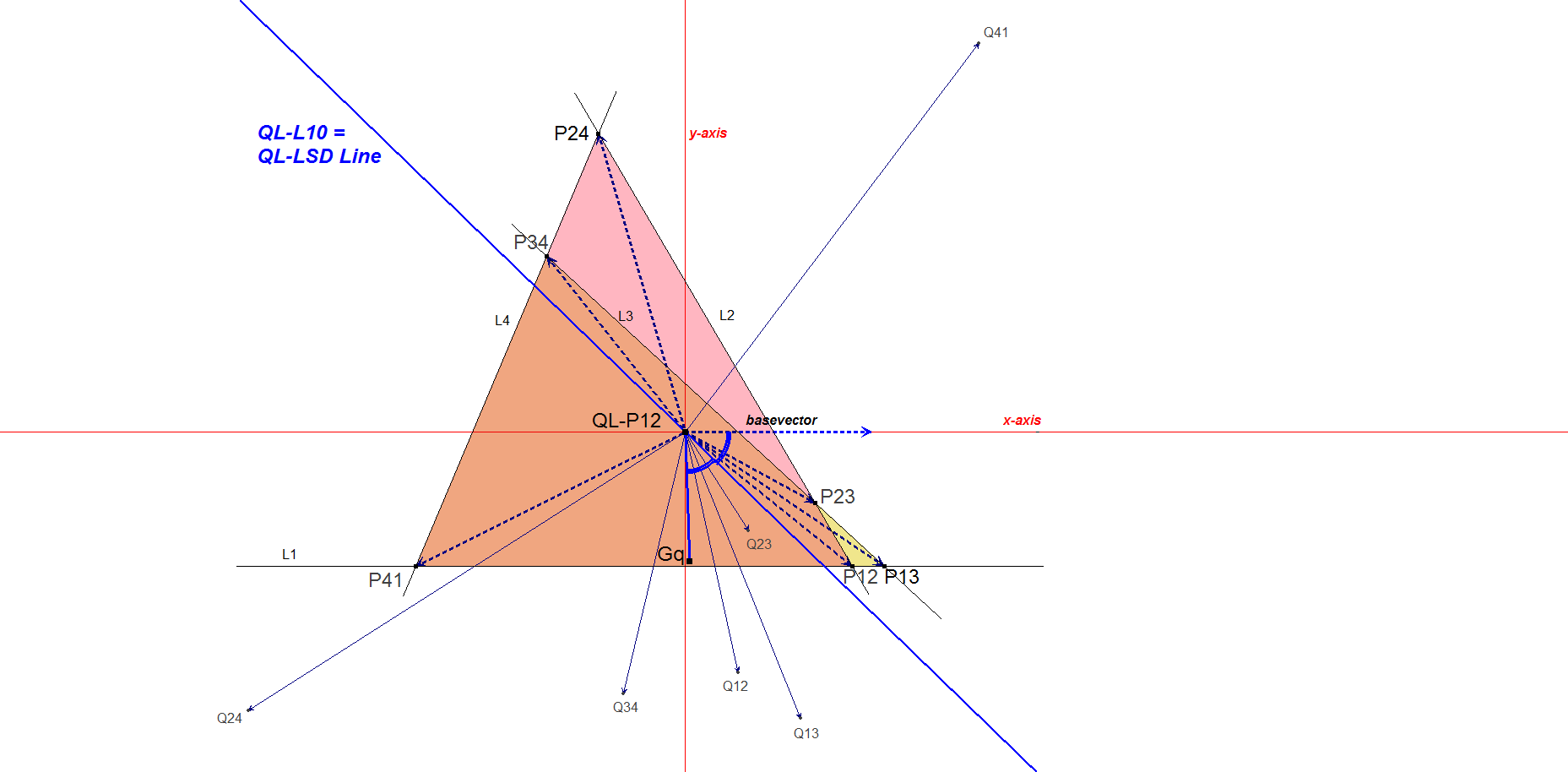
- Draw a random couple of perpendicular lines intersecting in QL-P12 as x-axis and y-axis.
- Let the 6 vertices Pij of the QL be represented by complex numbers zi = xi + i yi.
- The Centroid of the QA-vertices is the point QL-P12 where z = 0.
- Let Gq = Centroid of the points Qij represented by zi2.
- The searched LSD line is the angle bisector of the x-axis and the line Gq.QL-P12.
CT-Coordinates of QL-L10
(-2 Ux Wx + Tz Wy + Ty Wz – W (( l – m) Vz Wy + ( l – n) Vy Wz) :
+Tz Wx – 2 Uy Wy + Tx Wz – W ((m – n) Vx Wz + (m – l) Vz Wx) :
+Ty Wx + Tx Wy – 2 Uz Wz – W ((n – l) Vy Wx + (n – m) Vx Wy) )
Where:
W=Sqrt[a4 (l-m)2 (l-n)2 Wb Wc+b4 (l-m)2 (m-n)2 Wa Wc+c4 (l-n)2 (m-n)2 Wb Wa
-2 a2 c2 (l-m) (l-n)2 (m-n) Wb WB-2 a2 b2 (l-m)2 (l-n) (m-n) Wc WC-2 b2 c2 (l-m) (l-n) (m-n)2 Wa WA],
Wa=(5 l4-8 l3 m+8 l2 m2-8 l3 n+10 l2 m n-12 l m2 n+8 l2 n2-12 l m n2+9 m2 n2),
Wb=(8 l2 m2-8 l m3+5 m4-12 l2 m n+10 l m2 n-8 m3 n+9 l2 n2-12 l m n2+8 m2 n2),
Wc=(9 l2 m2-12 l2 m n-12 l m2 n+8 l2 n2+10 l m n2+8 m2 n2-8 l n3-8 m n3+5 n4),
WA=(6 l2 m2-3 l m3-7 l2 m n-2 l m2 n+2 m3 n+6 l2 n2-2 l m n2+m2 n2-3 l n3+2 m n3),
WB=(3 l3 m-6 l2 m2-2 l3 n+2 l2 m n+7 l m2 n-l2 n2+2 l m n2-6 m2 n2-2 l n3+3 m n3),
WC=(2 l3 m+l2 m2+2 l m3-3 l3 n-2 l2 m n-2 l m2 n-3 m3 n+6 l2 n2-7 l m n2+6 m2 n2),
Wx=Sqrt[-a2 (l-m) (l-n) Vy Vz-b2 (l-m) (m-n) VA Vz+c2 (l-n) (m-n) Vy VA],
Wy=Sqrt[+a2 (l-m) (l-n) VB Vz-b2 (l-m) (m-n) Vx Vz+c2 (l-n) (m-n) Vx VB],
Wz=Sqrt[-a2 (l-m) (l-n) Vy VC+b2 (l-m) (m-n) Vx VC-c2 (l-n) (m-n) Vx Vy ],
Vx=(l2-2 l m-2 l n+3 m n), Vy=(-2 l m+m2+3 l n-2 m n), Vz=(3 l m-2 l n-2 m n+n2),
VA=(5 l2-4 l m-4 l n+3 m n), VB->(4 l m-5 m2-3 l n+4 m n), VC->(3 l m-4 l n-4 m n+5 n2),
Ux=a2 (l-m) (l-n) (l m+l n-m n) (l2-l m+m2-l n-m n+n2) (3 l m2-4 l m n-m2 n+3 l n2-m n2)-c2 (l-n) (m-n) (15 l5 m2-24 l4 m3+18 l3 m4-6 l2 m5-20 l5 m n+3 l4 m2 n+18 l3 m3 n-20 l2 m4 n+9 l m5 n+15 l5 n2+3 l4 m n2-12 l3 m2 n2+12 l2 m3 n2-3 l m4 n2-3 m5 n2-24 l4 n3+39 l3 m n3-30 l2 m2 n3+6 l m3 n3+3 m4 n3+6 l3 n4-11 l2 m n4+9 l m2 n4-3 m3 n4)+b2 (l-m) (m-n) (15 l5 m2-24 l4 m3+6 l3 m4-20 l5 m n+3 l4 m2 n+39 l3 m3 n-11 l2 m4 n+15 l5 n2+3 l4 m n2-12 l3 m2 n2-30 l2 m3 n2+9 l m4 n2-24 l4 n3+18 l3 m n3+12 l2 m2 n3+6 l m3 n3-3 m4 n3+18 l3 n4-20 l2 m n4-3 l m2 n4+3 m3 n4-6 l2 n5+9 l m n5-3 m2 n5),
Uy=b2 (m-l) (m-n) (l m-l n+m n) (l2-l m+m2-l n-m n+n2) (3 l2 m-l2 n-4 l m n-l n2+3 m n2)+c2 (l-n) (m-n) (6 l5 m2-18 l4 m3+24 l3 m4-15 l2 m5-9 l5 m n+20 l4 m2 n-18 l3 m3 n-3 l2 m4 n+20 l m5 n+3 l5 n2+3 l4 m n2-12 l3 m2 n2+12 l2 m3 n2-3 l m4 n2-15 m5 n2-3 l4 n3-6 l3 m n3+30 l2 m2 n3-39 l m3 n3+24 m4 n3+3 l3 n4-9 l2 m n4+11 l m2 n4-6 m3 n4)-a2 (l-m) (l-n) (6 l4 m3-24 l3 m4+15 l2 m5-11 l4 m2 n+39 l3 m3 n+3 l2 m4 n-20 l m5 n+9 l4 m n2-30 l3 m2 n2-12 l2 m3 n2+3 l m4 n2+15 m5 n2-3 l4 n3+6 l3 m n3+12 l2 m2 n3+18 l m3 n3-24 m4 n3+3 l3 n4-3 l2 m n4-20 l m2 n4+18 m3 n4-3 l2 n5+9 l m n5-6 m2 n5),
Uz=c2 (l-n) (m-n) (l m-l n-m n) (l2 m+l m2-3 l2 n+4 l m n-3 m2 n) (l2-l m+m2-l n-m n+n2)+a2 (l-m) (l-n) (3 l4 m3-3 l3 m4+3 l2 m5-9 l4 m2 n-6 l3 m3 n+3 l2 m4 n-9 l m5 n+11 l4 m n2+30 l3 m2 n2-12 l2 m3 n2+20 l m4 n2+6 m5 n2-6 l4 n3-39 l3 m n3+12 l2 m2 n3-18 l m3 n3-18 m4 n3+24 l3 n4-3 l2 m n4-3 l m2 n4+24 m3 n4-15 l2 n5+20 l m n5-15 m2 n5)-b2 (l-m) (m-n) (3 l5 m2-3 l4 m3+3 l3 m4-9 l5 m n+3 l4 m2 n-6 l3 m3 n-9 l2 m4 n+6 l5 n2+20 l4 m n2-12 l3 m2 n2+30 l2 m3 n2+11 l m4 n2-18 l4 n3-18 l3 m n3+12 l2 m2 n3-39 l m3 n3-6 m4 n3+24 l3 n4-3 l2 m n4-3 l m2 n4+24 m3 n4-15 l2 n5+20 l m n5-15 m2 n5),
Tx=c2 (l-n) (m-n) (8 l5 m2-21 l4 m3+24 l3 m4-10 l2 m5-17 l5 m n+29 l4 m2 n-12 l3 m3 n-20 l2 m4 n+20 l m5 n+9 l5 n2+6 l4 m n2-30 l3 m2 n2+30 l2 m3 n2-6 l m4 n2-15 m5 n2-18 l4 n3+18 l3 m n3+20 l2 m2 n3-45 l m3 n3+33 m4 n3+18 l3 n4-50 l2 m n4+53 l m2 n4-24 m3 n4)+a2 (l-m) (l-n) (9 l3 m4+l4 m2 n-39 l3 m3 n-5 l m5 n+l4 m n2+48 l3 m2 n2+12 l2 m3 n2+19 l m4 n2-39 l3 m n3+12 l2 m2 n3-48 l m3 n3+3 m4 n3+9 l3 n4+19 l m2 n4+3 m3 n4-5 l m n5)-b2 (l-m) (m-n) (9 l5 m2-18 l4 m3+18 l3 m4-17 l5 m n+6 l4 m2 n+18 l3 m3 n-50 l2 m4 n+8 l5 n2+29 l4 m n2-30 l3 m2 n2+20 l2 m3 n2+53 l m4 n2-21 l4 n3-12 l3 m n3+30 l2 m2 n3-45 l m3 n3-24 m4 n3+24 l3 n4-20 l2 m n4-6 l m2 n4+33 m3 n4-10 l2 n5+20 l m n5-15 m2 n5),
Ty=-c2 (l-n) (m-n) (10 l5 m2-24 l4 m3+21 l3 m4-8 l2 m5-20 l5 m n+20 l4 m2 n+12 l3 m3 n-29 l2 m4 n+17 l m5 n+15 l5 n2+6 l4 m n2-30 l3 m2 n2+30 l2 m3 n2-6 l m4 n2-9 m5 n2-33 l4 n3+45 l3 m n3-20 l2 m2 n3-18 l m3 n3+18 m4 n3+24 l3 n4-53 l2 m n4+50 l m2 n4-18 m3 n4)+b2 (l-m) (m-n) (-9 l4 m3+5 l5 m n+39 l3 m3 n-l2 m4 n-19 l4 m n2-12 l3 m2 n2-48 l2 m3 n2-l m4 n2-3 l4 n3+48 l3 m n3-12 l2 m2 n3+39 l m3 n3-3 l3 n4-19 l2 m n4-9 m3 n4+5 l m n5)+a2 (l-m) (l-n) (18 l4 m3-18 l3 m4+9 l2 m5-50 l4 m2 n+18 l3 m3 n+6 l2 m4 n-17 l m5 n+53 l4 m n2+20 l3 m2 n2-30 l2 m3 n2+29 l m4 n2+8 m5 n2-24 l4 n3-45 l3 m n3+30 l2 m2 n3-12 l m3 n3-21 m4 n3+33 l3 n4-6 l2 m n4-20 l m2 n4+24 m3 n4-15 l2 n5+20 l m n5-10 m2 n5),
Tz=-c2 (l-n) (m-n) (-3 l4 m3-3 l3 m4+5 l5 m n-19 l4 m2 n+48 l3 m3 n-19 l2 m4 n+5 l m5 n-12 l3 m2 n2-12 l2 m3 n2-9 l4 n3+39 l3 m n3-48 l2 m2 n3+39 l m3 n3-9 m4 n3-l2 m n4-l m2 n4)+b2 (l-m) (m-n) (15 l5 m2-33 l4 m3+24 l3 m4-20 l5 m n+6 l4 m2 n+45 l3 m3 n-53 l2 m4 n+10 l5 n2+20 l4 m n2-30 l3 m2 n2-20 l2 m3 n2+50 l m4 n2-24 l4 n3+12 l3 m n3+30 l2 m2 n3-18 l m3 n3-18 m4 n3+21 l3 n4-29 l2 m n4-6 l m2 n4+18 m3 n4-8 l2 n5+17 l m n5-9 m2 n5)-a2 (l-m) (l-n) (24 l4 m3-33 l3 m4+15 l2 m5-53 l4 m2 n+45 l3 m3 n+6 l2 m4 n-20 l m5 n+50 l4 m n2-20 l3 m2 n2-30 l2 m3 n2+20 l m4 n2+10 m5 n2-18 l4 n3-18 l3 m n3+30 l2 m2 n3+12 l m3 n3-24 m4 n3+18 l3 n4-6 l2 m n4-29 l m2 n4+21 m3 n4-9 l2 n5+17 l m n5-8 m2 n5).
Properties
- QL-P12 lies on QL-L10.
- There is no line with largest sum of squared distances. However when looking for the line with largest sum of squared distances passing through QL-P12, then the line through QL-P12 perpendicular to QL-L10 will be the line with this property.
Estimated human page views: 1136
