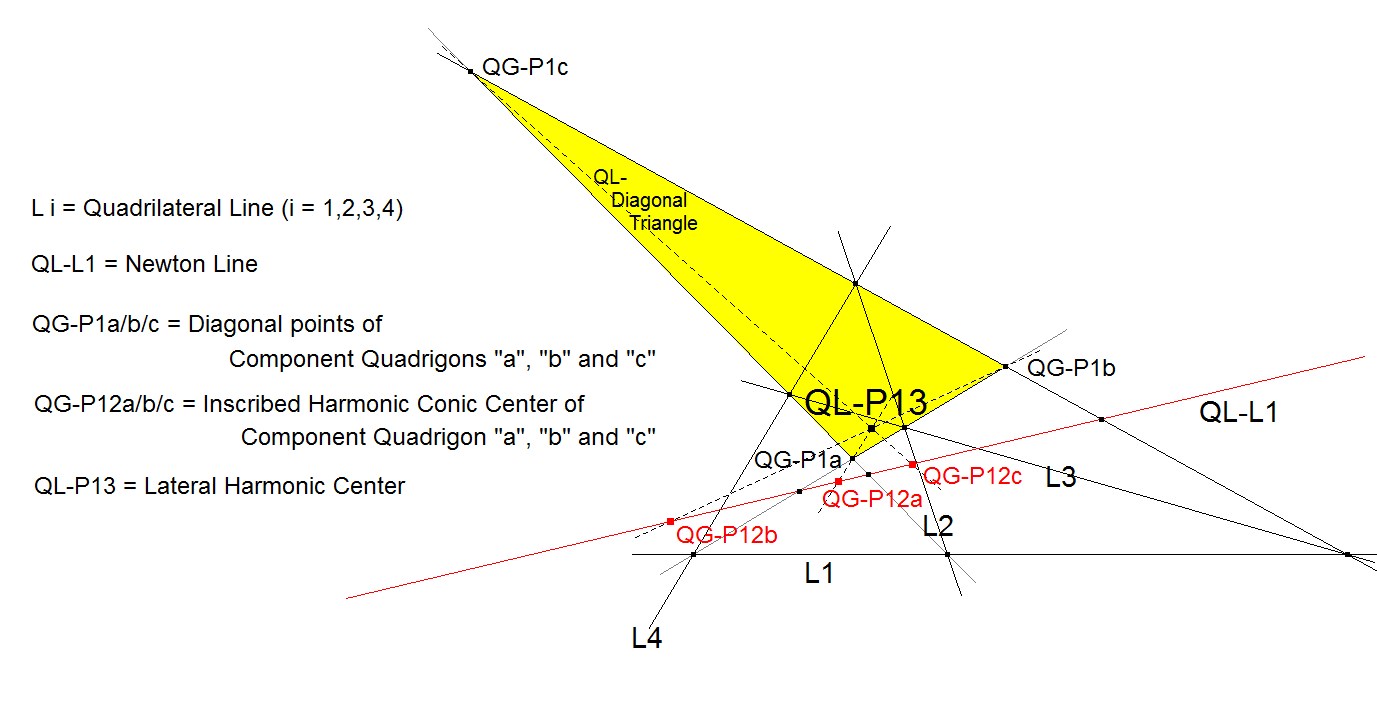
QL-P13: QL-Harmonic Center or Lateral Harmonic Center
The QL-Harmonic Center or Lateral Harmonic Center is the Perspector of:
QL-P13 is named harmonic because its construction is based on projective principles leading to harmonic properties.
Another construction:
1. Let QG-P2a, QG-P2b, QG-P2c be the Midpoints of the diagonals of a quadrilateral. These points are collinear at the Newton Line (QL-L1). See QG-P2 and QL-L1.
2. The triangle bounded by the lines QG-P2a.QG-P1a, QG-P2b.QG-P1b, QG-P2c.QG-P1c is perspective with the QL-Diagonal Triangle (QG-P1a.QG-P1b.QG-P1c). Their perspector is QL-P13.
Coordinates:
1st CT-coordinate:
m n (3 m n - l m - l n) (note that this formula is independent of a,b,c)
1st DT-coordinate:
1 / l2
Properties:
- QL-P13 lies on QL-P17.QL-P24.
- QL-P13 is collinear with QA-P16, QG-P1, QG-P12 and QG-P13 (see QG-L2).
- The 3 variants of QG-L2 in a Quadrilateral concur in QL-P13.
- QL-P13 is the Radical Center of the 3 Cross Diagonal Circles and the Circumcircle of the QL-Diagonal Triangle (QL-Tr1). A Cross Diagonal Circle is a circle passing through two ends of one QL-diagonal and the intersection point of the two other QL-diagonals. See Ref-11, Hyacinthos Message # 12896 from Quang Tuan Bui.
- QL-P13 is also the Perspector of the triangles formed by the 3 QL-versions resp. of QG-P1 and QG-P12.
- QL-P13 is also the Perspector of the triangle bounded by the 3 QL-versions of the connecting lines of QG-P1 and QG-P2 and the triangle formed by the 3 QL-versions of QG-P1 (which is the QL-Diagonal Triangle).
- Let L1L2L3L4 be a Quadrilateral. According to the definition of Diagonal Triangle QL-Tr1 each Component Triangle CTi (formed by lines Lj,Lk,Ll) is perspective with QL-Tr1 with perspectrix Li. Let the corresponding perspector be Pi. Let Qi (i=1,2,3,4) be the center of the circumconic to QL-Tr1 with perspector Pi. QL-P13 is the common intersection point of lines Pi.Qi (in analogy to the QA-property of QA-P16 from Angel Montesdeoca, January 18, 2015).