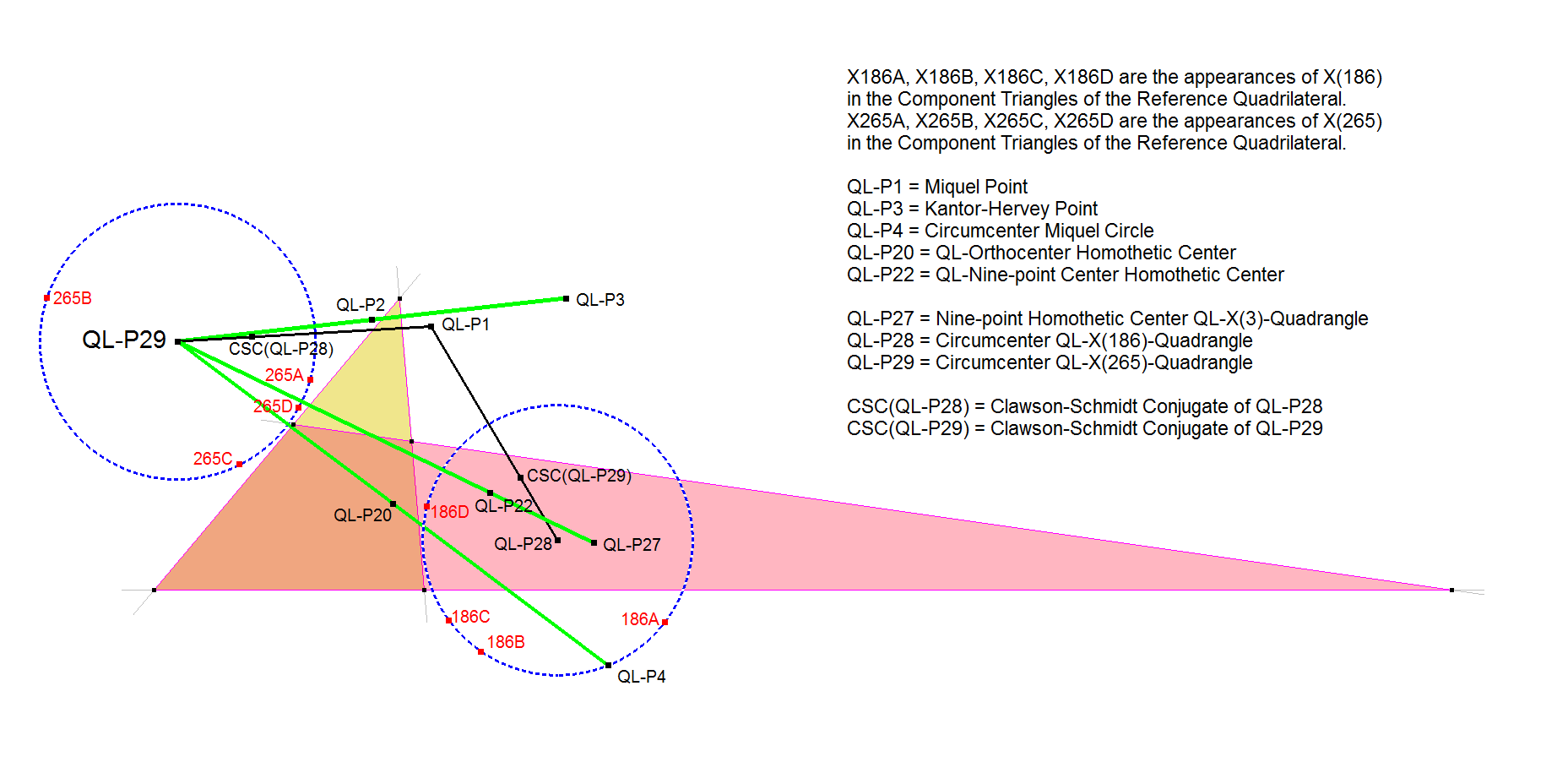
QL-P29: Circumcenter QL-X(265)-Quadrangle
QL-P29 is the Circumcenter of the circle through the four X(265) points of the Component Triangles of the Reference Quadrilateral, also called the QL-CT-versions of X(265).
X(265) = the Isogonal Conjugate of X(186), where:
X(186) is the Inverse of the Orthocenter X(4) in the circumcircle of a triangle.
See Ref-12 for an explanation of ETC-points X(i).
See Ref-33 Anopolis message # 409 for a discussion on this point.
There actually are 3 Triangle-points in ETC in the range X(1)-X(4000) for which their appearances in the Component Triangles of a Quadrilateral are concyclic: X(3), X(186), X(265). Only for X(4) these appearances are collinear in this range.
It’s remarkable that these points all relate to X(3) and X(4).
-Quadrangle-01.png)
Coordinates:
1st CT-coordinate:
a4 l (-2 l m + m2 + 2 l n - n2)
+ (b2 - c2) (m - n) (b2 (l2 - 2 l m + m n) - c2 (l2 - 2 l n + m n))
- a2 c2 (l m2 + (l2 - 4 l m + m2) n + l n2)
+ a2 b2 (l m (l + m) - 4 l m n + (l + m) n2)
1st DT-coordinate:
a4 (m - n) (m + n) (-5 l4 + 3 m2 n2 + l2 (m2 + n2))
- b4 (m2 - n2)2 (l2 + 3 m2)
+ c4 (m2 - n2)2 (l2 + 3 n2)
+ 2 a2 b2 (-m4 n2 + 3 m2 n4 + l4 (m2 + n2) + l2 (3 m4 - 8 m2 n2 + n4))
- 2 a2 c2 ( 3 m4 n2 - m2 n4 + l4 (m2 + n2) + l2 (m4 - 8 m2 n2 + 3 n4))
Properties:
- QL-P29 lies on these lines:
- The QL-X(265) circle is the Clawson-Schmidt Conjugate (QL-Tf1) of the QL-X(186) circle.
- QL-Tf1(QL-P28) = Inverse of QL-P1 in QL-X(186) circle, QL-Tf1(QL-P29) = Inverse of QL-P1 in QL-X(265) circle.
- QL-P29 lies on the line QL-P1.QL-Tf1(QL-P28), as well as QL-P28 lies on the line QL-P1.QL-Tf1(QL-P29),
- moreover: QL-P28.QL-Tf1(QL-P29) : QL-Tf1(QL-P29).QL-P1 = QL-P29.QL-Tf1(QL-P28) : QL-Tf1(QL-P28).QL-P1.
- QL-Tf1(QL-P4) = The Reflection of QL-P1 in the Steiner line (QL-L2) and lies on the QL-X(265) circle.
- Radius of the QL-X(265) circle = length line segment QL-P1.QP-P3.
- Radius QL-X(186)circle : Radius QL-X(265)circle = QL-P1.QL-P28 : QL-P1.QL-P29.
- The 5 versions of the QL-X(265) circle in a 5-Line (Pentalateral) all pass through a common point. See Ref-34, QFG#82 by Seiichi Kirikami.
- QL-P29 is the 4L-p2 point as described in Morley’s document Ref-49, paragraph 3.
- The QL-P29-Triple Triangle in a Quadrangle is perspective with the QL-P2-Triple Triangle as well as the QL-P3-Triple Triangle with perspector QA-P15.