QL-P30: Morley’s Second Circle Center
Morley mentions in his paper how in an n-Line (system of n random lines) in a recursive way several centers can be constructed. In his terminology this Second Circle Center is the ratiopoint nL-Center Circle Center : nL-Second Orthocenter ((n-2) : 1).
QL-P30 is used for constructing Morley’s Second Orthocenter in a 5-Line.
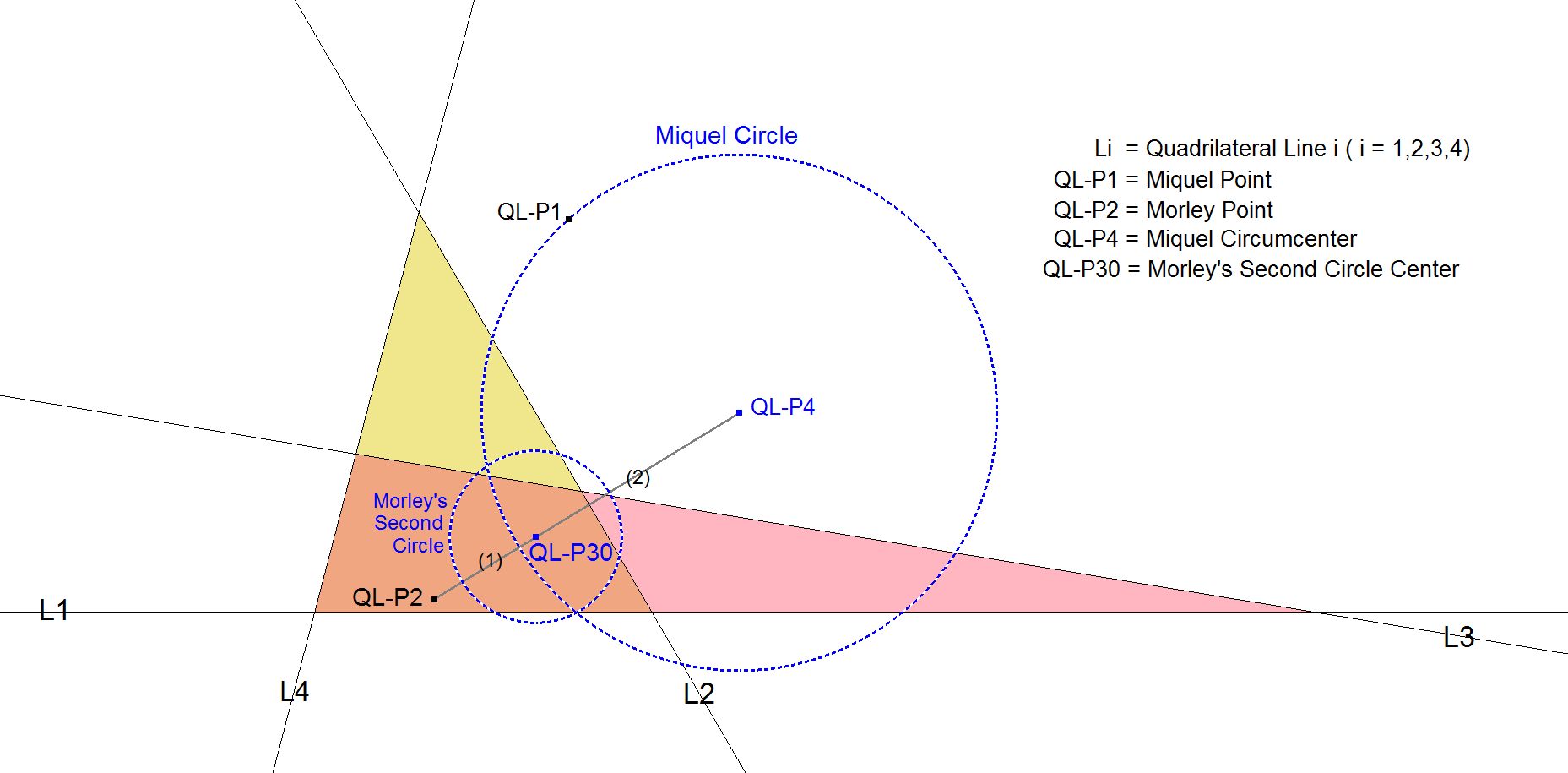
The Miquel Circle in a Quadrilateral is the equivalent of the circumcircle in a triangle.
Morley’s Second Circle in a Quadrilateral is the equivalent of the Nine-point Circle in a triangle.
1st CT-coordinate:
+ a4 (m - n) (-l2 + m n) + b4 (l - 2 m) (l - n) (m - n) + c4 (l - m) (l - 2 n) (m - n)
- b2 c2 (m - n) (2 l2 - 3 l m - 3 l n + 4 m n) + a2 b2 (l - n) (2 m2 + l n - 3 m n) - a2 c2 (l - m) (l m - 3 m n + 2 n2)
Properties:
- QL-P30 lies on these lines:
- QL-P30 is the center of Morley’s Second Circle.
- QL-P30 is used for the construction of 5L-Morley’s Second Orthocenter.