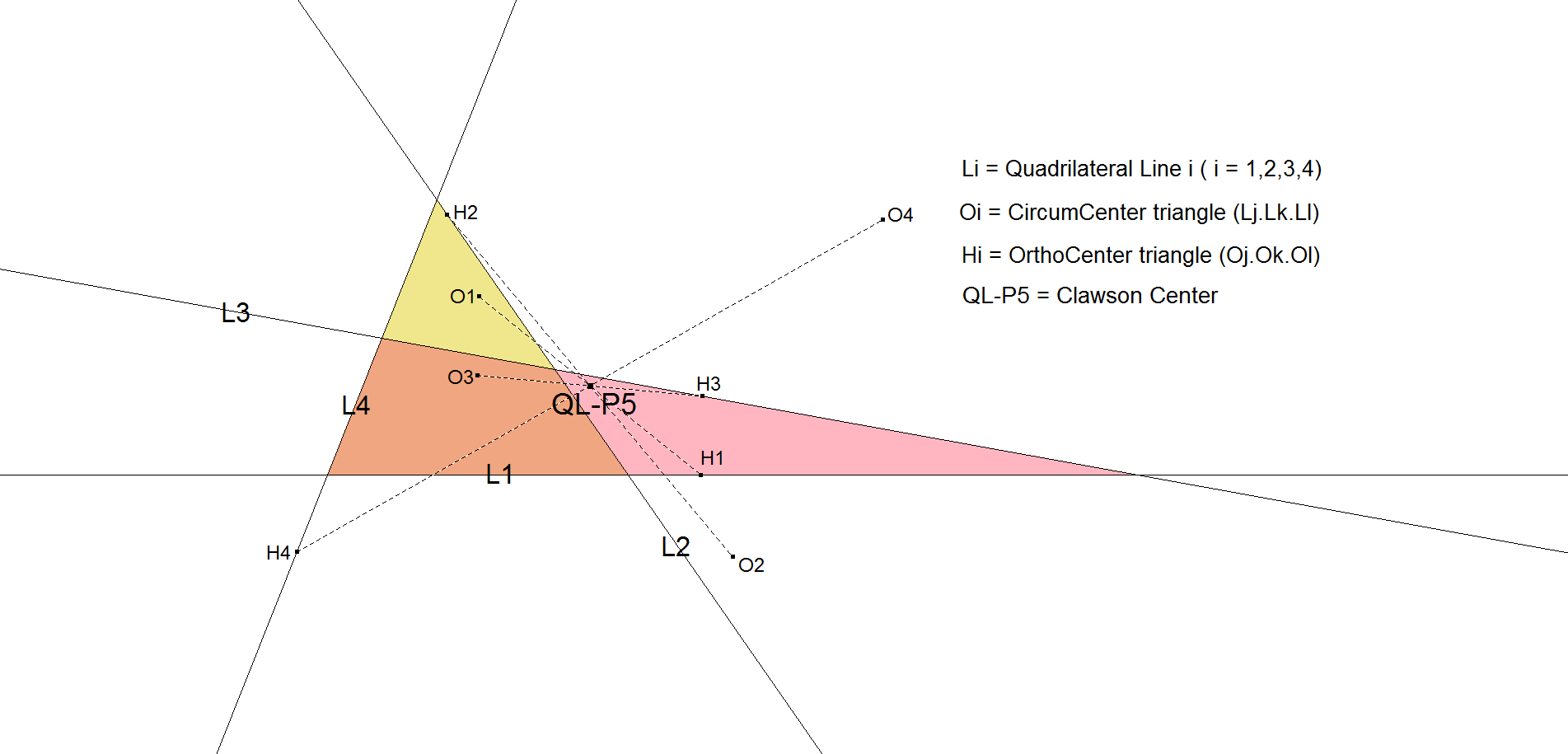
QL-P5: Clawson Center
This point was mentioned by J.W. Clawson. In his document [31] this point is referred to as the “Orthic Center” of the Circumcenter Quadrangle.
The Circumcenter Quadrangle is defined by the circumcenters O1, O2, O3, O4 of the 4 component triangles Li.Lj.Lk of the Reference Quadrilateral L1.L2.L3.L4. These 4 circumcenters are concyclic on the Miquel Circle. The Orthocenters H1, H2, H3, H4 of the Component Triangles Oi.Oj.Ok of the Circumcenter Quadrangle O1.O2.O3.O4 again are concyclic (on the Hervey Circle with circumcenter QL-P3 the Kantor-Hervey Point).
Now QL-P5 is the common midpoint of Oi.Hi (i=1,2,3,4).
Since Quadrangles O1.O2.O3.O4 and H1.H2.H3.H4 are homothetic it also can be said that QL-P5 is the center of homothecy of Quadrangles O1.O2.O3.O4 and H1.H2.H3.H4.
1st CT-coordinate
l (m – n) (a2 SA l + b2 SB m + c2 SC n + 8 Δ2 (m n – l m – l n) / l)
1st DT-coordinate
-(m2-n2) (+Sa2 (m2-n2)2 + Sb2 (l2-n2)2 +Sc2 (l2-m2)2
+2 (Sb Sc l4+Sa Sc m4+Sa Sb n4) + 2 S2(l2 (m2+n2)-3 m2 n2))
Properties
- QL-P5 lies on these lines:
- QL-P5 is the Reflection of QL-P4 in QL-P6.
- QL-P5 is the Reflection of QL-P20 in QL-P22.
- The distance ratios between points QL-P20, QL-P22, QL-P12, QL-P5 are 3 : 1 : 2.
- QL-P5 is the shared Euler-Poncelet Point (QA-P2) from the Circumcenter Quadrangle and from the Orthocenter Quadrangle in the Circumcenter Quadrangle (resp. O1.O2.O3.O4 and H1.H2.H3.H4 in picture QL-P3).
- d(QL-P5 , QL-P12) = d(QL-P2 , QL-P3) / 3 (d = distance)
- QL-P5 is the Center QL-Ci5 (Plücker Circle).
- QL-P5 = Anticenter (see [13]) of (concyclic) circumcenters of the 4 component triangles of the Reference Quadrilateral O1.O2.O3.O4 (note Randy Hutson).
- QL-P5 = Anticenter (see [13]) of (concyclic) orthocenters H1.H2.H3.H4 of 4 component triangles of above quadrangle (note Randy Hutson).
- The 3 QA-versions of QL-P5 are collinear on a line parallel to QA-L4 (note Eckart Schmidt).
- In a Quadrangle are collinear the 3 QA-versions of QL-P5 & the circumcenter of the QL-P1 Triple Triangle & the Orthocenter of the QL-P6 Triple Triangle & QA-Tf2(QA-P3).
- QL-P5 is the common point of the 4 Simson lines of Oi wrt Triangle Oj.Ok.Ol, where (i,j,k,l) ∈ (1,2,3,4) and O1, O2, O3, O4 are the 4 Orthocenters of the Component Triangles of the Reference Quadrangle (Seiichi Kirikami, August, 2012).
- The QA-Orthopole(QA-Tf3) of QL-Ci5 is a circle through QL-P5.
- Let X3i (i=1,2,3,4) be the circumcenters of the triangles (Lj,Lk,Ll), where j,k,l=different numbers from (1,2,3,4) unequal i. Let L3i be the lines through X3i parallel to Li. QL-P5 is the Homothetic Center of the Reference Quadrilateral and (L31,L32, L33, L34). This construction is similar to the construction of QL-P20 and QL-P22.
Estimated human page views: 768
