QL-27Qu1: Morley’s Multiple Cardioids
It is possible to construct a Cardioid inscribed in a Quadrilateral:
There even are 27 ways to inscribe a Cardioid in a Quadrilateral.
These Cardioids were described in F. Morley’s document “Extensions of Clifford’s Chain-Theorem”. See [37].
He also describes that in a Quadrilateral (4-Line) one single Cardioid will occur enveloping the 4 circumcircles of the Component Triangles (QL-Qu1).
Last but not least he predicts the numbers of other epicycloids occurring in a n-Line.
27 Cardioids inscribed in a Quadrilateral:
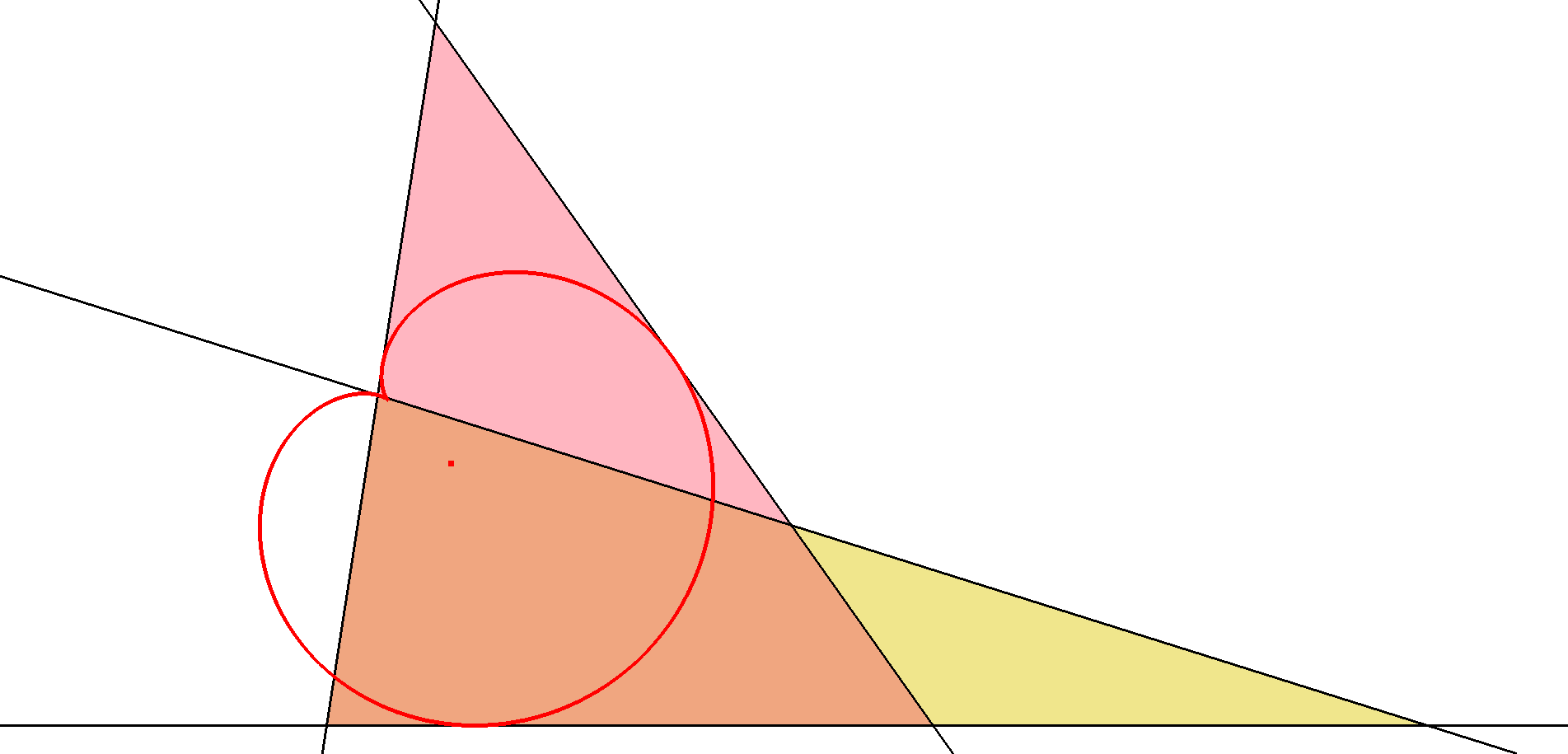
4 Times 3 equilateral triangles in a Quadrilateral are needed to construct them:
The 27 red intersections of the (extended) sides of the 4×3 equilateral triangles are the centers of the inscribed Cardioids. Each center is the intersection point of 4 sidelines.
More information about the subject also can be found in Bernard Keizer’s document at [43].
Construction
For the construction of the Cardioids we shall first determine per Cardioid its Center and its Cusp as follows:
- Construct for each Component Triangle its 1st, 2nd and 3rd Morley Triangles. See [13].
- This gives per Component Triangle 3 x 3 parallel lines each intersecting at 60°.
- Since the Reference Quadrilateral has 4 different Component Triangles the total amount of lines is 4 x 3 x 3. These 36 lines intersect somehow in 27 points, where each of these points is intersected by 4 lines. These 27 points are the Centers of the 27 Cardioids we are looking for. This property was described by F. Morley in [37].
- Let one of these Centers have barycentric coordinates (u : v : w) wrt one of the Component Triangles. Then the cusp has barycentric coordinates (b2 c2 u3 : a2 c2 v3 : a2 b2 w3). Found by Eckart Schmidt, see [34], QFG-message # 55. Construct the Cusp by using this property.
- Knowing the Cardioid Center P and the Cardioid Cusp P1 it is possible to construct the Cardioid:
- Let S1 be a variable point on circle Ci(P,P1).
- Let S2 be the reflection of P1 in line P.S1.
- Let S3 be the reflection of S2 in S1.
- The locus of S3 with variable point S1 is the Cardioid.
Equation QL-27Qu1 in CT-notation
Pending
Equation QL-27Qu1 in DT-notation
Pending
Properties
- The 27 Centers of QL-27Qu1 lie on Eckart’s Cubic QL-Cu2.
- The centers of Morley’s Multiple Cardioids are called incenters by Morley in [37]. There he states that the 27 incenters lie on a network of 36 axes, being the 4×9 Morley axes of the QL-Component Triangles. Each incenter is intersected by 4 axes and each axis contains 3 incenters. See also [34], QFG-messages #1462, #1463.
Estimated human page views: 815
