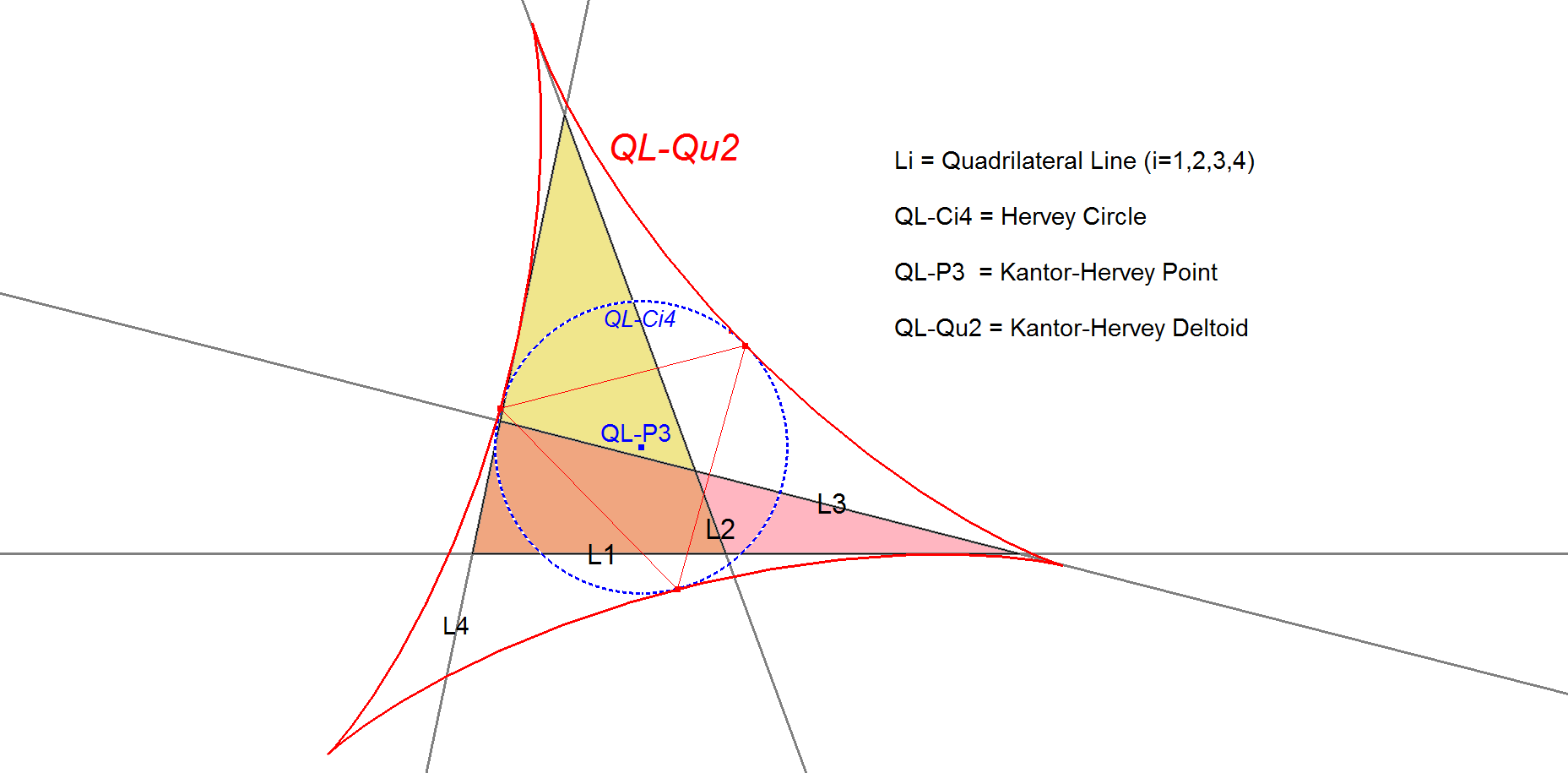
QL-Qu2: Kantor-Hervey Deltoid
Ql-Qu2 is the only Deltoid that can be constructed tangent to the four lines of a Quadrilateral.
This Deltoid was used by Kantor and Hervey in order to prove their theorem that point QL-P3 was belonging to the 4 perpendicular bisectors of the Euler segments of the reference triangles. It seems they are the oldest reference for this Deltoid. See reference at [38].
More information about the subject also can be found in Bernard Keizer’s document at [43] as well as in QFG # 514 [34].
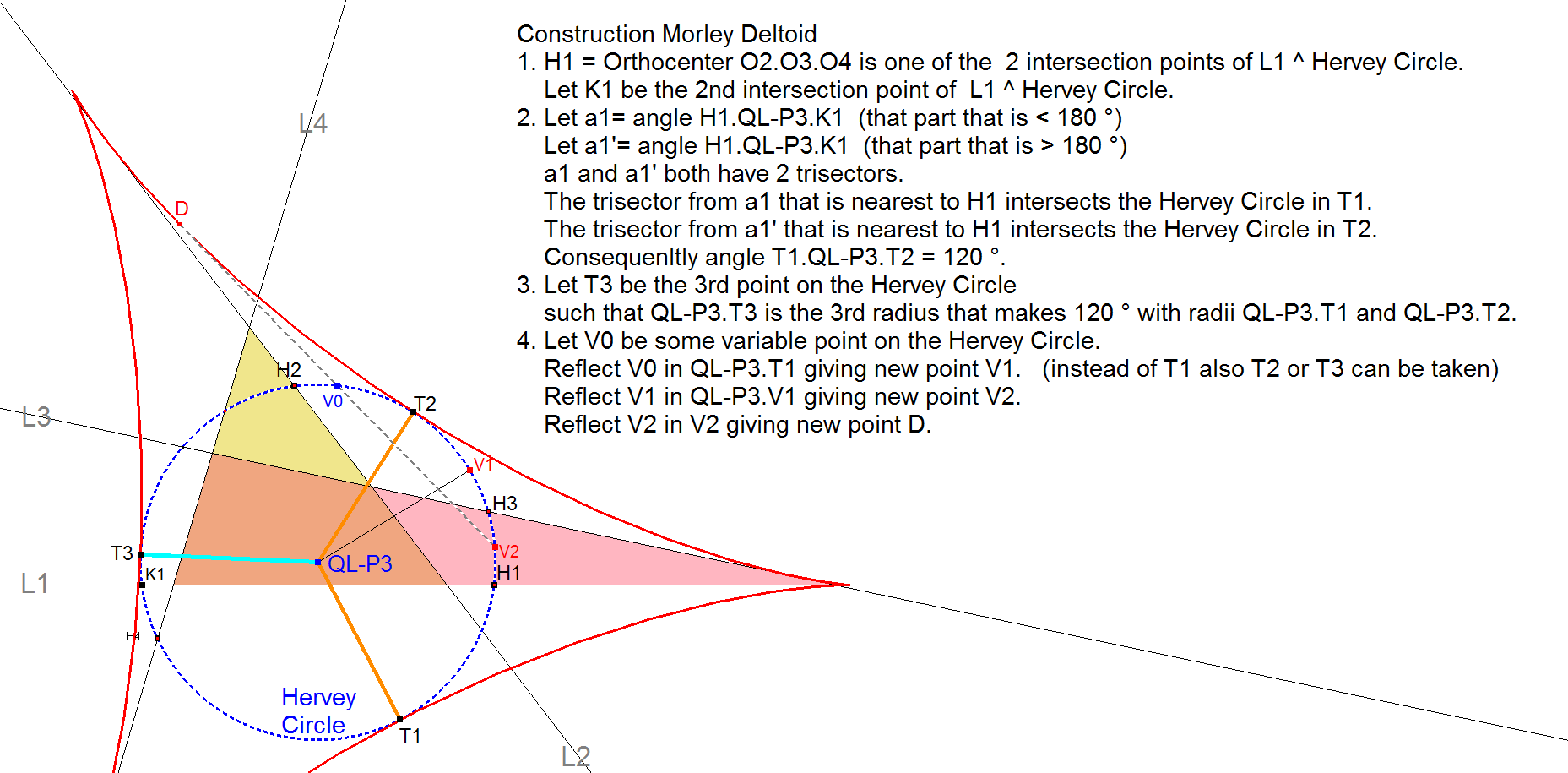
Construction
Another construction can be found at [34], QFG messages # 522 and 529:
- Let P be a point on QL-L2,
- Let line L be the perpendicular bisector of P.QL-P1,
- Let O = QL-Tf1(P),
- Let line T be parallel to L through the reflection of O in QL-P5.
- The lines T envelope QL-Qu2.
A construction of the axes of QL-Qu2 can be found at QFG messages # 535 and 541.
Equation QL-Qu2 in CT-notation (Bernard Gibert, August 15, 2013):
SIM4 (x + y + z)4
+ 4 SIM3 MED (x + y + z)3 B3L
+ 2 SIM2 MED2 (x + y + z)2 C3L
+ 4 SIM MED3 (x + y + z) K3L
+ MED4 H3 = 0
where:
SIM = c2 (l + m) (l – n) (m – n) – b2 (l – m) (m – n) (l + n) + a2 (l – m) (l – n) (m + n)
MED = (l – m) (m – n) (n – l)
B3L = b2 x – c2 x – a2 y + c2 y + a2 z – b2 z
C3L = -2 b2 c2 (3 x2 – 3 x y – 3 x z – 2 y z) + c4 (3 x2 – 6 x y + 3 y2 – z2) + b4 (3 x2 – y2 – 6 x z + 3 z2) + a4 (-x2 + 3 y2 – 6 y z + 3 z2) + a2 (2 c2 (3 x y – 3 y2 + 2 x z + 3 y z) + 2 b2 (2 x y + 3 x z + 3 y z – 3 z2))
K3L = b6 (x – z) (x – y – z) (x + y – z) – c6 (x – y) (x – y – z) (x – y + z) + a6 (y – z) (x + y – z) (x – y + z) – b4 c2 (x – y – z) (3 x2 – y2 – 3 x z – 7 y z) + b2 c4 (x – y – z) (3 x2 – 3 x y – 7 y z – z2) + a4 (c2 (x – y + z) (x2 – 3 y2 + 7 x z + 3 y z) – b2 (x + y – z) (x2 + 7 x y + 3 y z – 3 z2)) + a2 (-4 b2 c2 (x – y) (x – z) (y – z) + b4 (x + y – z) (7 x y + y2 + 3 x z – 3 z2) – c4 (x – y + z) (3 x y – 3 y2 + 7 x z + z2))
H3 = b8 (x – y – z)2 (x + y – z)2 + c8 (x – y – z)2 (x – y + z)2 + a8 (x + y – z)2 (x – y + z)2 – 4 b6 c2 (x – y – z)2 (x2 + x y – x z – 4 y z) – 4 b2 c6 (x – y – z)2 (x2 – x y + x z – 4 y z) + 2 b4 c4 (x – y – z)2 (3 x2 – y2 – 14 y z – z2) + a6 (-4 c2 (x – y + z)2 (x y + y2 – 4 x z – y z) + 4 b2 (x + y – z)2 (4 x y – x z + y z – z2)) + a4 (-2 b4 (x + y – z)2 (x2 + 14 x y + y2 – 3 z2) – 2 c4 (x – y + z)2 (x2 – 3 y2 + 14 x z + z2) + 4 b2 c2 (x4 + 7 x3 y – x2 y2 – 7 x y3 + 7 x3 z + 48 x2 y z + 7 x y2 z + 2 y3 z – x2 z2 + 7 x y z2 – 4 y2 z2 – 7 x z3 + 2 y z3)) + a2 (4 c6 (x – y + z)2 (x y – y2 + 4 x z – y z) + 4 b6 (x + y – z)2 (4 x y + x z – y z – z2) – 4 b4 c2 (7 x3 y + x2 y2 – 7 x y3 – y4 – 2 x3 z – 7 x2 y z – 48 x y2 z – 7 y3 z + 4 x2 z2 – 7 x y z2 + y2 z2 – 2 x z3 + 7 y z3) + 4 b2 c4 (2 x3 y – 4 x2 y2 + 2 x y3 – 7 x3 z + 7 x2 y z + 7 x y2 z – 7 y3 z – x2 z2 + 48 x y z2 – y2 z2 + 7 x z3 + 7 y z3 + z4))
Properties
- QL-P3 is the Center of the Deltoid.
- QL-Ci4, the Hervey Circle is the inscribed circle of the Deltoid (note Bernard Keizer, 2013).
- QL-Qu2 is not only tangent to L1, L2, L3, L4 but also to the line parallel to the Newton Line QL-L1 through the Reflection of QL-P1 in QL-P5 (note Bernard Keizer, 2013), which is the asymptote of QL-Cu1 (see [34], Bernard Keizer, QFG#2517).
- The 3 axes of QL-Qu2 (through QL-P3 and the 3 cusps) are parallel to the 3 asymptotes of Eckart’s Cubic QL-Cu2 (Eckart Schmidt, May 9, 2013).
- A congruent QL-Deltoid can be constructed with its cusps in the same direction with center QL-P4 and inscribed circle QL-Ci3. See [34], QFG#514.
Estimated human page views: 729
